Kooperativität

Kooperativität, ein Begriff aus der Biochemie, charakterisiert die Funktion von Transportproteinen (darunter Rezeptoren) und von Enzymen, die aus mehreren Untereinheiten bestehen (so genannten „oligomeren Proteinen“).

Definition

Proteine aus mehreren ähnlichen Untereinheiten zeigen häufig das Phänomen der Kooperativität: die Bindungsstärke eines Liganden hängt davon ab, wie viele der restlichen Untereinheiten bereits einen Liganden tragen. Wird die Bindung zunehmend stärker, ergibt sich das gut untersuchte Phänomen der positiven Kooperativität. Behindern sich die Liganden gegenseitig, so dass die letzten Bindungsplätze mit niedriger Affinität eingenommen werden, folgt das weniger bekannte (aber ebenso häufige) Phänomen der negativen Kooperativität. Der erste Fall wirkt wie ein Schalter (Proteine mit Liganden an allen Bindungsstellen und Proteine ganz ohne Liganden beherrschen die Szene, teilgesättigte Proteine sind unterrepräsentiert). Im zweiten Fall ist der Bindungsgrad der Proteine gleichmäßiger und hängt von der Ligandenkonzentration ab.

Prototyp eines allosterischen Proteins mit positiver Kooperativität ist das aus vier Untereinheiten bestehende (tetramere) Hämoglobin. Im Unterschied zum monomeren Sauerstoff-Trägerprotein Myoglobin bindet Hämoglobin außer Sauerstoff (O₂) noch Protonen (H⁺), Kohlendioxid (CO₂) und Chloridionen. Die Bindungseigenschaften von Sauerstoff an das Tetramer (das in der Abbildung vereinfachend als Dimer dargestellt wird) werden vielfältig moduliert:

Die Bindung von O₂ begünstigt die Bindung weiterer O₂-Moleküle an dasselbe Hämoglobinmolekül;
die Bindungsstärke des O₂ ist pH-abhängig. Neben einer steigenden Wasserstoffionenkonzentration fördert auch eine steigende CO₂-Konzentration die O₂-Abgabe. Genau diese Signale verwendet der Muskel, um seinen Sauerstoffbedarf zu signalisieren,
schließlich wird die Abgabe von Sauerstoff noch durch ein spezielles Regulatormolekül – im Menschen ist dies 2,3-Bisphosphoglycerat (2,3-BPG; Kreis auf dem T-Zustand) – gefördert. Die Regulierung der Sauerstoffversorgung über 2,3-BPG ist für die Versorgung eines Fötus und für die Versorgung des Menschen unter den Bedingungen großer Höhen (Bergsteiger!) von herausragender Bedeutung

So erzwingen alle genannten Liganden (bis auf O₂ selbst) die Abgabe von Sauerstoff, das heißt, den Übergang der hochaffinen R-Konformation in die niederaffine T-Konformation. Die nachfolgende Abbildung zeigt das Prinzip dieser Regulation: der Konformationsübergang von T (tense) zu R (relaxed) wird dadurch ausgelöst, dass der Sauerstoff das zentrale Eisenatom (Fe⁺⁺, brauner Kreis) im Häm (roter Balken) in die Ebene zieht. Andere Proteingruppen Aminosäurereste folgen dieser Bewegung, wodurch Wasserstoffbrücken gebrochen und die sog. “Bohr-Protonen” (H⁺) sowie CO₂ freigesetzt werden.

kooperatives Bindungsverhalten

Nachweis und Beschreibung

Kooperativ bindende Proteine (Carrier, Rezeptoren, Enzyme) folgen nicht dem Prinzip der Sättigungshyperbel: sie weisen entweder ein "sigmoides" (positive Kooperativität) oder ein "pseudohyperboles" Bindungsverhalten (negative Kooperativität) auf. Nur aufgrund der unauffälligen, einer Hyperbel ähnelnden Charakteristik wurde und wird die negative Kooperativität häufig übersehen.

Die Bindungskurven

das Phänomen der Kooperativität lässt sich nach Adair durch Funktionen beschreiben, denen zwei Km-Werte, K(1) und K(2), zukommen. Diese komplexen Funktionen lassen sich wiederum als Übergang zwischen zwei Sättigungshyperbeln (1 und 2, d.h. schwarze Kurven in der folgenden Abbildung) verstehen:

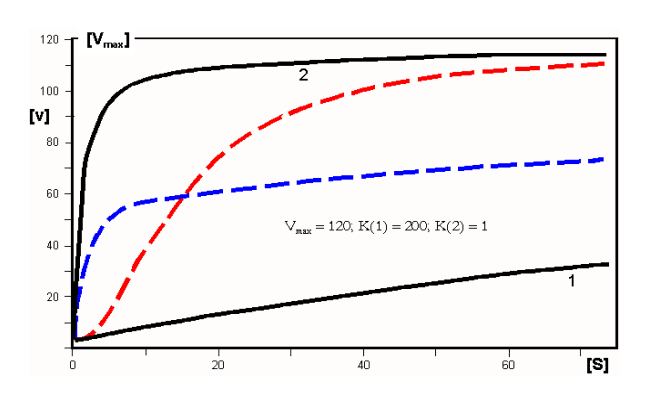
kooperative Übergänge

Positive Kooperativität: im Grundzustand (T) erfolgt Bindung zunächst gemäß der Hyperbel 1 (niedere Affinität). Dann geschieht der Übergang in den hochaffinen Zustand (R), so dass weitere Liganden gemäß der Hyperbel 2 binden. Der Übergang zwischen diesen Zuständen entspricht der roten Linie, die eine deutlich sigmoide Form hat und leicht zu diagnostizieren ist. Die gezeigte Kurve entspricht einem Hill-Koeffizienten von 1,92;
Negative Kooperativität: zu verstehen als der umgekehrte Übergang zwischen einem Zustand hoher Affinität (kleinen Km-Wertes; Hyperbel 2) auf einen solchen niederer Affinität (hohen Km-Wertes; Hyperbel 1). Der Übergang zwischen diesen Zuständen entspricht der blauen Linie, die einer Hyperbel zu gleichen scheint, aber davon verschieden ist: sie ist durch einen Hill Koeffizienten n_H = 0,63 charakterisiert.

Negative Kooperativität wurde zunächst für die Bindung von NAD⁺ durch Glycerinaldehyd-3-phosphat-dehydrogenase (GAPDH) entdeckt.

Halbseitenreaktivität (engl. half-of-the-sites reactivity): extreme Form der negativen Kooperativität, bei der ein oligomeres Enzym mit 2n Bindungsstellen (nahezu) ausschließlich an n Bindungsstelle(n) mit dem Substrat reagiert.

Linearisierungen

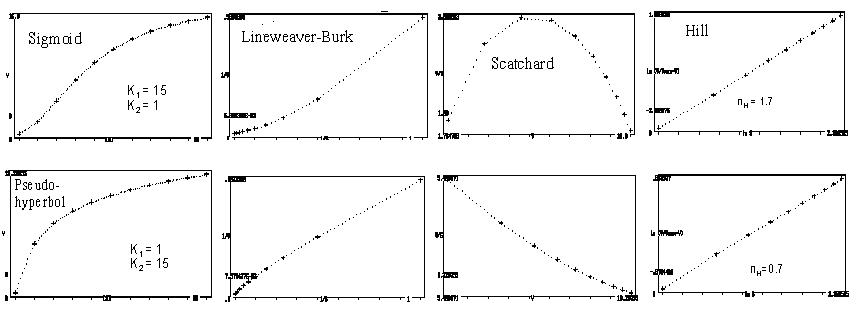
Eindeutige Hinweise auf Kooperativität findet man, wenn man die Bindungskurven den unter "Enzymkinetik" beschriebenen "Linearisierungsverfahren" unterwirft: hier ergeben sich charakteristische Abweichungen von einer Geraden – besonders augenfällig im Falle des Scatchard-Diagramms. Diese Abweichungen werden am ehesten im Hill-Diagramm nivelliert, das aber End-Äste von 45° (Steigung = 1) aufweisen würde, wenn im oberen und unteren Bereich der Substratkonzentrationen genügend Messpunkte vorlägen. Nur im Falle n_H = n (maximale Kooperativität) würden diese entfallen:

der Hill-Koeffizient, n_H, beschreibt das Maß der Kooperativität und kann die Zahl der interagierenden Untereinheiten (n) nicht überschreiten. Für Hämoglobin (n = 4) beträgt n_H = 2,9, abgeleitet aus der Steigung am Nulldurchgang.
für negative Kooperativität liegt n_H < 1

Die beste Bestimmung der Kooperativitätsparameter erfolgt heute auf dem Wege der "nichtlinearen Regression" unter Verwendung

der Hill-Gleichung, d.h. einer erweiterten Michaelis-Menten Gleichung: Parameter n_H und K₅₀ (Substratkonzentration, bei der 50 % Sättigung erreicht ist);
der Adair-Gleichung: Parameter K_T und K_R (Dissoziationskonstanten für den "T" und den "R-Zustand"). Die Beispiele der nachfolgenden Sättigungsfunktionen wurden für die Werte

K_T = 15, K_R = 1 errechnet:

Kooperativitätsphänomene

Hill-Koeffizient

Mit der Hill-Gleichung kann die Kooperativität der Bindung quantitativ beschrieben werden. Dabei wird der Anteil der Sättigung der Ligandenbindungsstellen als Funktion der Ligandenkonzentration dargestellt. Der Hill-Koeffizient ist ein Maß für die Steilheit der Kurve.

$n_{H}=\mathrm {\frac {\log(81)}{\log(EC_{90}/EC_{10})}}$

mit EC90 und EC10 für die Messwerte bei 10 % bzw. 90 % der maximalen Sättigung.

Response-Koeffizient

Bei sigmoidalen Kurven ist der Hill-Koeffizient zu ungenau, weshalb der Response-Koeffizient verwendet wird:

$R(x)={\frac {x}{y}}{\frac {dy}{dx}}$

Der Zusammenhang zwischen Hill-Koeffizient und Response coefficient ist folgender:

$n_{H}=2{\frac {\int _{\mathrm {\log(EC_{10})} }^{\mathrm {\log(EC_{90})} }R_{f}(I)d(\log I)}{\mathrm {\log(EC_{90})-\log(EC_{10})} }}=2\langle R_{f}\rangle _{\mathrm {EC_{10},EC_{90}} }$

mit $\langle X\rangle _{a,b}$ als Mittelwert der Variablen X im Bereich [a,b].

Basierend auf einem Artikel in:

Wikipedia.de