
Asymptote
Eine Asymptote (altgr. ἀσύμπτωτος asýmptōtos „nicht übereinstimmend“, von altgr. πίπτω> pípto „ich falle“) ist in der Mathematik eine Linie (Kurve, häufig als Gerade), der sich der Graph einer Funktion im Unendlichen immer weiter annähert. Eine „Sonderform“ ist der Asymptotische Punkt, bei dem die Annäherung nicht im Unendlichen stattfindet. Bei den vertikalen Asymptoten gibt es die Besonderheit, dass sie sich nicht als Funktion beschreiben lassen.
Das Antonym Symptote ist nicht gebräuchlich.
Eine verbreitete Auffassung, dass sich eine Funktion der Asymptote zwar nähert, sie aber niemals schneidet, stimmt nur für einen Teil der Funktionen mit asymptotischem Verhalten. Es gibt nämlich Funktionen, die ihre Asymptote ein oder mehrere Male in ihrem Verlauf schneiden (und sich ihr erst dann nähern, ohne sie nochmals zu schneiden). Und es gibt Funktionen, die um ihre Asymptote oszillieren und sie somit unendlich oft schneiden.
Asymptoten einer reellen Funktion
Sei
die zu betrachtende Funktion, deren Definitionsbereich
eine Teilmenge der reellen
Zahlen
ist.
sei deren Asymptote (Ausnahme: Asymptotischer Punkt, weiter unten).
Parallel zur in diesem Artikel gewählten Gliederung der Asymptoten nach ihrer Form und Lage kann man Asymptoten – beziehungsweise das Verhalten einer Funktion zur Asymptote – auch wie folgt unterscheiden:
- horizontale Annäherung: der horizontale (waagerechte) Abstand Δx
zwischen Funktion und Asymptote geht gegen Null…
- …in Richtung unendlich großer/kleiner
:
Dies gilt für vertikale gerade Asymptoten. - …in Richtung eines Punktes:
Dies gilt für den Asymptotischen Punkt.
- …in Richtung unendlich großer/kleiner
- vertikale Annäherung: der vertikale (senkrechte) Abstand Δy
zwischen Funktion
und Asymptote
geht gegen Null…
- …in Richtung unendlich großer/kleiner
:
Mathematisch wird dies mittels Grenzwert ausgedrückt:oder
Dies gilt für alle anderen Geraden Asymptoten (horizontale und schräge) sowie die Nichtgeraden Asymptoten. - …in Richtung eines Punktes:
Dies gilt für den Asymptotischen Punkt.
- …in Richtung unendlich großer/kleiner
Gerade Asymptoten
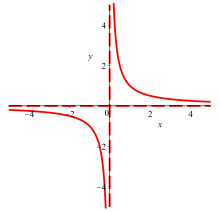
Gerade Asymptoten können in drei Typen unterschieden werden: vertikale, horizontale und schiefe.
Vertikale Asymptote
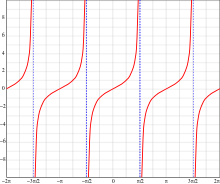
Vertikale (oder „senkrechte“) Asymptoten sind Geraden, die parallel zur
y-Achse verlaufen. Einem
wären in diesem Falle mehrere
„zugeordnet“. Entsprechend lassen sich solche Geraden nicht als Graph einer Funktion
beschreiben. Vertikale Asymptoten werden über die Gleichung
beschrieben. Im Punkt
schneidet die vertikale Asymptote die x-Achse des Koordinatensystems.
Eine zu betrachtende Funktion
hat eine solche vertikale Asymptote, wenn der Funktionswert
an einer Stelle
gegen unendlich läuft. Anders gesagt: Nähert man sich auf der x-Achse von links
oder rechts der Stelle
,
so geht
gegen positiv oder negativ Unendlich. Mathematisch lässt sich dies wie folgt
ausdrücken:
,
oder
.
Im Unterschied zu anderen im Artikel angesprochenen Asymptoten ,
werden hier Grenzwerte gegen eine relle Zahl und nicht gegen
untersucht. Daher kann eine reelle Funktion auch mehrere vertikale Asymptoten
besitzen. Beispiele solcher Funktionen sind Tangens und
Kotangens.
Eine vertikale Asymptoten einer reellen Funktion liegt immer an einer Singularität.
Handelt es sich bei der Singularität um eine Polstelle,
so nennt man die vertikale Asymptote auch Polgerade. Es gibt allerdings auch
Asymptoten an wesentlichen
Singularitäten also an Punkten, die keine Polstellen sind. Ein Beispiel
dafür ist die Funktion .
Horizontale Asymptote
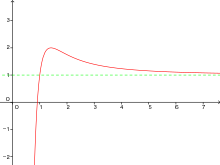
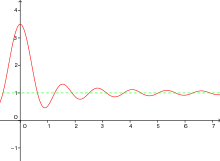
Horizontale (oder „waagerechte“) Asymptoten sind Geraden, die parallel zur x-Achse verlaufen. Sie können über die Gleichung
beschrieben werden. Dies entspricht einer Geradengleichung
der Form
mit
.
Als Funktion geschrieben haben horizontale Asymptoten die Form
.
Der Wert
entspricht dann dem
in der Geradengleichung. Im Punkt
schneidet die horizontale Asymptote die y-Achse des Koordinatensystems.
Eine zu betrachtende Funktion
hat eine solche horizontale Asymptote, wenn der Funktionswert
im positiven oder negativen Unendlichen gegen den Wert
läuft. Mathematisch lässt sich diese Bedingung mittels Grenzwert
ausdrücken:
oder
Und dies analog den schiefen Asymptoten als Differenz geschrieben wäre dann:
oder
Bekannte Funktionen mit einer horizontalen Asymptote sind Exponential- und Hyperbelfunktionen.
Die letztgenannten Hyperbeln, wie zum Beispiel
sind das klassisches Beispiel für Funktionen mit vertikaler und
horizontaler Asymptote:
- Die vertikale Asymptote dieser Funktion ist die Gerade
, die die x-Achse an der Stelle
schneidet, was gleichzeitig die Polstelle dieser Hyperbelfunktion darstellt. Anders ausgedrückt: Der Schnittpunkt der vertikalen Asymptote mit der x-Achse ist in
, was dem Ursprung des Koordinatensystems entspricht.
- Die horizontale Asymptote dieser Funktion ist die Gerade
, mit also
. Die y-Achse wird folglich im Punkt
geschnitten, also ebenfalls im Koordinatenursprung.
Schiefe Asymptoten
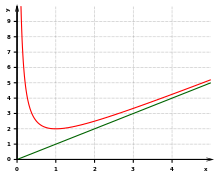
Schiefe (oder „schräge“, „geneigte“) Asymptoten lassen sich mittels der Geradengleichung:
mit
oder als Funktion:
darstellen. Wichtig hierbei: ,
sonst wäre es eine horizontale Asymptote. Und wie man es von solchen linearen Funktionen
kennt, läuft der Graph von
in x- und y-Richtung gegen Unendlich.
Eine zu betrachtende Funktion
hat eine solche schiefe Asymptote
,
wenn sie sich dieser im Unendlichen annähert. Diese Bedingung/Eigenschaft sieht
mathematisch wie folgt aus:
oder
Anders gesagt: Eine Annäherung im Unendlichen heißt, dass der senkrechte
Abstand zwischen Funktion und ihrer Asymptote im Unendlichen gegen Null läuft.
Mathematisch stellt ein Abstand eine Differenz dar. Betrachtet man also diese
Differenz zwischen der Funktion
und ihrer Asymptote
so läuft die Differenz im Unendlichen gegen Null:
oder
Nichtgerade Asymptoten
Nicht nur Geraden können Asymptoten zu einer Funktion sein, sondern auch nichtgerade Kurven oder Funktionen. So können zum Beispiel beliebige Polynome (Quadratische Funktionen etc.) Asymptoten zu anderen Funktionen sein. Und wie schon oben für die geraden Asymptoten (außer den vertikalen) beschrieben, gilt auch hier:
oder
Ist beispielsweise
eine zu betrachtende rationale
Funktion (mit den Polynomen
und
),
so erhält man deren Asymptote
aus dem „Ganzteil“ der Polynomdivision
von
durch
.
Des Weiteren hat die Funktion vertikale Asymptoten durch ihre Polstellen.
Anmerkung: Der senkrechte Abstand von
zu
wird durch den „Restteil“ der Polynomdivision beschrieben. Dieser ist eine echt
gebrochenrationale Funktion, die dieselben vertikalen Asymptoten wie
hat und zusätzlich noch die horizontale Asymptote
besitzt. Letzteres beschreibt noch einmal die Eigenschaft einer Asymptote: Wenn
die Abstandsfunktion (Abstand zwischen Funktion
und ihrer Asymptote
)
eine horizontale Asymptote bei
hat, so nähert sich der Abstand zwischen Funktion und ihrer Asymptote im
Unendlichen gegen Null.
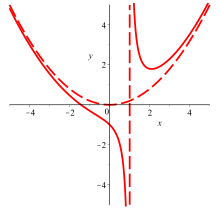
Ein Beispiel (siehe auch Abbildung rechts):
Diese Beispielfunktion hat folgende Asymptoten:
- eine vertikale Asymptote
durch ihre Polstelle und
- die Parabel
, die man aus dem „Ganzteil“ des Ergebnisses der Polynomdivision erhält. Eine Parabel als Asymptote nennt man dann Näherungsparabel. Dieser nähert sich die betrachtete Funktion
im Unendlichen an.
Asymptotischer Punkt
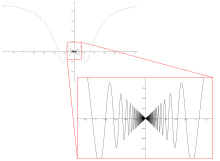
Statt einer Kurve oder Geraden können sich Funktionen auch nur einem Punkt
asymptotisch nähern. In diesem Fall gilt nicht die Bedingung der oben
beschrieben „linienartigen“ Asymptoten, bei denen sich die Funktion
erst im Unendlichen der Asymptote annähert. Hier ist ein Punkt
im „Endlichen“ die Asymptote.
Asymptoten weiterer Kurven
Neben obigen Funktionsgraphen stetiger
Funktionen
mit abzählbar
unendlich vielen Definitionslücken
– dies trifft auf die meisten in der Schule betrachteten Funktionen zu – gibt es
noch weitere mathematische Objekte, die ein asymptotisches Verhalten aufweisen
können, dazu zählen Wege
oder allgemeiner algebraische
Kurven wie zum Beispiel Spiralen
oder Klothoide.
Für eine algebraische Kurve lässt sich der Asymptotenbegriff aus Sicht der projektiven Geometrie auch als eine Tangente im Unendlichen beschreiben.
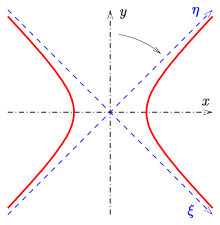
Ein Beispiel einer algebraischen Kurve mit zwei schiefen Asymptoten ist eine Hyperbel, die durch die Gleichung
mit den beiden Konstanten
und
definiert ist. Die Asymptoten
und
der Hyperbel können durch
und
beschrieben werden.
Man kann die Hyperbel auch durch zwei Funktionsgleichungen (für die obere und untere „Halbhyperbel“)
und
beschreiben. Auf diese Funktionen kann man die Erkenntnisse aus dem ersten Teil des Artikels anwenden.
Weitere Beispiele:
-
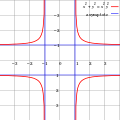 Graph einer Kurve mit mehreren horizontalen und vertikalen Asymptoten
Graph einer Kurve mit mehreren horizontalen und vertikalen Asymptoten -
 Das Kartesisches Blatt – eine ebene algebraische Kurve mit einer schiefen Asymptote
Das Kartesisches Blatt – eine ebene algebraische Kurve mit einer schiefen Asymptote -
 Zwei offene Wege, die sich einem geschlossenen Weg asymptotisch nähern.
Zwei offene Wege, die sich einem geschlossenen Weg asymptotisch nähern. -
 Ein offener Weg, der sich einem asymptotischen Punkt nähert.
Ein offener Weg, der sich einem asymptotischen Punkt nähert.
Siehe auch
Literatur
- Hans-Jochen Bartsch: Taschenbuch mathematischer Formeln für Ingenieure und Naturwissenschaftler. Hanser, 2014, ISBN 9783446437357, S. 449–450
- Guido Walz: Lexikon der Mathematik: Band 1: A bis Eif. Springer, 2016, ISBN 9783662534984, S. 121–122


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 22.10. 2021