Massenwirkungsgesetz

Das Massenwirkungsgesetz (Abkürzung „MWG“) definiert das chemische Gleichgewicht für chemische Reaktionen. Dem Massenwirkungsgesetz zufolge ist das Produkt aus den Aktivitäten $a_{i}$ der beteiligten Stoffe ${\textstyle i}$ (potenziert mit den jeweiligen stöchiometrischen Zahlen $\nu _{i}$ ) konstant. Die Konstante wird als Gleichgewichts- oder Massenwirkungskonstante bezeichnet. Sind an einer Reaktion Stoffe beteiligt, erhält man:

$K=\prod _{i=1}^{z}a_{i}^{{\nu }_{i}}$

Hierbei ist ${\textstyle \prod }$ das Produktzeichen. Da die stöchiometrischen Zahlen der Ausgangsstoffe negativ sind, werden Massenwirkungsgesetze als Brüche formuliert, wobei die Produktterme den Zähler und die Eduktterme den Nenner bilden. Für eine Reaktion mit der unter Verwendung des Gleichgewichtspfeils formulierten stöchiometrischen Reaktionsgleichung

$|\nu _{\mathrm {A} }|\,\mathrm {A} +|\nu _{\mathrm {B} }|\,\mathrm {B} +\ldots +|\nu _{\mathrm {M} }|\,\mathrm {M} \rightleftharpoons \nu _{\mathrm {N} }\,\mathrm {N} +\nu _{\mathrm {O} }\,\mathrm {O} +\ldots +\nu _{\mathrm {Z} }\,\mathrm {Z}$ ,

an der die Ausgangsstoffe A, B … M und die Produkte N, O … Z beteiligt sind, nimmt das Massenwirkungsgesetz daher folgende Form an:

$K={\frac {{a_{\text{N}}}^{\nu _{\text{N}}}\cdot {a_{\text{O}}}^{\nu _{\text{O}}}\cdot \ldots \cdot {a_{\text{Z}}^{\nu _{\mathrm {Z} }}}}{{a_{\text{A}}}^{|\nu _{\text{A}}|}\cdot {a_{\text{B}}}^{|\nu _{\text{B}}|}\cdot \ldots \cdot {a_{\text{M}}^{|\nu _{\mathrm {M} }|}}}}$

Die Gleichgewichtskonstante ist eine intensive dimensionslose thermodynamische Zustandsgröße und definiert diejenige stoffliche Zusammensetzung, für die das unter den jeweiligen Reaktionsbedingungen relevante thermodynamische Potential des reagierenden Systems ein Minimum aufweist. Stellt sich der durch das Massenwirkungsgesetz definierte Gleichgewichtszustand ein, wird die maximale Zunahme der Entropie, die durch Zustandsänderungen im Reaktionsgemisch realisierbar ist, erreicht.

Geschichte

Cato Maximilian Guldberg (links) und Peter Waage (rechts) im Jahr 1891

Das Massenwirkungsgesetz wurde von den norwegischen Chemikern Cato Maximilian Guldberg und Peter Waage experimentell ermittelt und 1864 in Norwegisch sowie 1867 in Französisch (mit ihren experimentellen Daten und einem modifizierten Gesetz) erstmals veröffentlicht. Ihre Veröffentlichung fand lange keine große Beachtung. Der Ire John Hewitt Jellett kam 1873 zu ähnlichen Schlussfolgerungen, ebenso wie 1877 Jacobus Henricus van ’t Hoff. Insbesondere nach den Veröffentlichungen von van ’t Hoff (aber auch von anderen wie August Friedrich Horstmann) hatten Guldberg und Waage den Eindruck, dass ihre Arbeit nicht genug bekannt sei. Nachdem sie 1879 im Journal für Praktische Chemie eine ausführlichere Darlegung in deutscher Sprache veröffentlicht hatten, erkannte van ’t Hoff deren Priorität an.

Thermodynamische Aspekte

Thermodynamische Definition der Gleichgewichtskonstante

Im thermodynamischen Gleichgewicht ist die Änderung des (zur Beschreibung des Systems angebrachten) thermodynamischen Potentials null. Die Gleichgewichtskonstante hängt dann lediglich von den gewählten (willkürlichen, aber festen) Referenzzuständen (o) der beteiligten Stoffe ab. Der Referenzzustand (o) kann entsprechend dem betrachteten Reaktionsszenario frei gewählt werden und ist nicht mit sogenannten Standardzuständen unter Standardbedingungen zu verwechseln. Die Lage des Gleichgewichtes sowie der Wert der Gleichgewichtskonstante hängen dabei vom gewählten Referenzzustand ab.

Da thermodynamische Gleichgewichtszustände unabhängig vom Weg sind, auf dem diese erreicht werden, ist es für die thermodynamische Gültigkeit des Massenwirkungsgesetzes nicht erforderlich, die unabhängigen Zustandsvariablen des relevanten thermodynamischen Potentials während des gesamten Reaktionsverlaufes konstant zu halten.

In der Praxis sind vor allem zwei Szenarien von Bedeutung:

Reaktionen, die in Autoklaven durchgeführt werden, wie etwa Solvothermalsynthesen, finden bei konstantem Volumen und in der Regel bei konstanter Temperatur statt, wohingegen der Druck variabel ist. Wird eine Reaktion bei konstanter Temperatur, konstantem Volumen und variablem Druck durchgeführt, ist die freie Energie (Helmholtz-Potential) F das relevante thermodynamische Potential, da neben der sich im Verlauf der chemischen Reaktion verändernden stofflichen Zusammensetzung des reagierenden Systems Temperatur und Volumen die unabhängigen Zustandsvariablen der freien Energie sind. Das Massenwirkungsgesetz definiert dann die stoffliche Zusammensetzung des reagierenden Systems, für die die freie Energie minimal wird und die damit den thermodynamischen Gleichgewichtszustand darstellt. Für eine chemische Reaktion, die in einem durch ein konstantes Volumen und eine konstante Temperatur gekennzeichneten Referenzzustand (o) durchgeführt wird und deren beteiligte Komponenten ${\textstyle i}$ in diesem Referenzzustand die molaren freien Bildungsenergien $F_{i,m}^{\circ }$ besitzen, wird die molare freie Reaktionsenergie $\Delta _{R}F^{\circ }$ gleich:

$\Delta _{R}F^{\circ }=\sum _{i=1}^{z}(\nu _{i}\cdot F_{i,m}^{\circ })$

Die Gleichgewichtskonstante ist dann unter Verwendung der absoluten Temperatur wie folgt durch die molare freie Reaktionsenergie des Referenzzustandes $\Delta _{R}F^{\circ }$ definiert:

$K=\exp {\bigg [}-{\frac {\Delta _{R}F^{\circ }}{R\cdot T}}{\bigg ]}.$

Viele chemische Reaktionen werden in offenen Systemen durchgeführt, so dass Druckausgleich zwischen dem reagierenden System und der Umgebung erfolgen kann. Somit kann angenommen werden, dass die betrachtete Reaktion unter einem konstanten, dem Umgebungsdruck entsprechenden Druck durchgeführt wird, während das Volumen des reagierenden Systems variabel ist. Wird eine Reaktion bei konstantem Druck, konstanter Temperatur und variablem Volumen durchgeführt, ist die freie Enthalpie (Gibbs-Energie) das relevante thermodynamische Potential, da neben der sich im Verlauf der chemischen Reaktion verändernden stofflichen Zusammensetzung des reagierenden Systems Druck und Temperatur die unabhängigen Zustandsvariablen der freien Enthalpie sind. In diesem Fall definiert das Massenwirkungsgesetz die stoffliche Zusammensetzung des reagierenden Systems, für die die freie Enthalpie minimal wird und die damit den thermodynamischen Gleichgewichtszustand darstellt. Für eine chemische Reaktion, die in einem durch einen konstanten Druck und eine konstante Temperatur gekennzeichneten Referenzzustand (o) durchgeführt wird und deren beteiligte Komponenten ${\textstyle i}$ in diesem Referenzzustand die molaren freien Bildungsenthalpien $G_{i,m}^{\circ }$ besitzen, wird die molare freie Reaktionsenthalpie $\Delta _{R}G^{\circ }$ gleich:

$\Delta _{R}G^{\circ }=\sum _{i=1}^{z}(\nu _{i}\cdot G_{i,m}^{\circ })$

Die Gleichgewichtskonstante ist dann wie folgt durch die molare freie Reaktionsenthalpie der Referenzzustände $\Delta _{R}G^{\circ }$ definiert:

$K=\exp {\bigg [}-{\frac {\Delta _{R}G^{\circ }}{R\cdot T}}{\bigg ]}$

Wird ein chemisches Gleichgewicht durch die Änderung der Konzentration eines an der betrachteten Reaktion beteiligten Stoffes – und damit seiner Aktivität – gestört, müssen sich gemäß dem Prinzip vom kleinsten Zwang nach Henry Le Chatelier die Aktivitäten (und damit die Konzentrationen) der anderen an der Reaktion beteiligten Stoffe so ändern, dass das Massenwirkungsgesetz erfüllt bleibt. Die Gleichgewichtskonstante ist somit unabhängig von den Ausgangskonzentrationen der an der betrachteten Reaktion beteiligten Stoffe. Als thermodynamische Zustandsgröße hängt die Gleichgewichtskonstante nicht vom Reaktionsmechanismus oder von kinetischen Größen wie Geschwindigkeitskonstanten und Reaktionsgeschwindigkeiten ab.

Herleitung

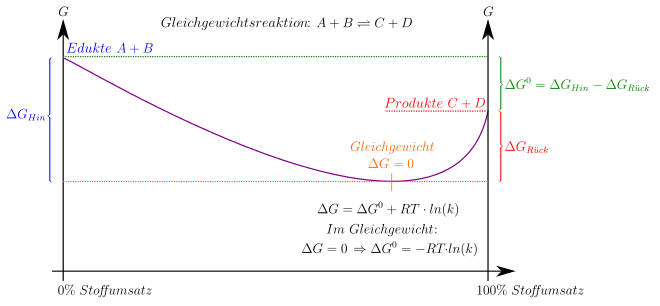
Profil der freien Enthalpie während einer Gleichgewichtsreaktion als Funktion des Umsatzes.

Im Folgenden wird exemplarisch angenommen, dass die betrachtete Reaktion bei einem durch einen konstanten Druck sowie eine konstante Temperatur gekennzeichneten Referenzzustand ( $\circ$ ) durchgeführt wird, so dass die freie Enthalpie das relevante thermodynamische Potential ist. Sinngemäß lässt sich die unten skizzierte Herleitung auf jedes andere thermodynamische Potential anwenden.

$G_{i}$ sei der Beitrag eines Stoffes zur extensiven freien Gesamtenthalpie $G_{\mathrm {sys} }$ des betrachteten Systems. Sofern Druck, Temperatur und die Stoffmengen $n_{j}$ aller weiteren anwesenden Stoffe konstant gehalten werden, ist das chemische Potential $\mu _{i}$ des Stoffes gleich der Änderung $\mathrm {d} G_{i}$ pro Änderung $\mathrm {d} n_{i}$ der Stoffmenge $n_{i}$ des Stoffes :

$\mu _{i}=\left({\frac {\partial G_{i}}{\partial {n_{i}}}}\right)_{T,p,n_{j\neq i}}$

Die Menge der Formelumsätze einer chemischen Reaktion in Mol ist durch die Umsatzvariable $\xi$ gegeben, dem Quotienten aus $\mathrm {d} n_{i}$ und der stöchiometrischen Zahl $\nu _{i}$ des Stoffes ${\textstyle i}$ :

$\mathrm {d} \xi ={\frac {\mathrm {d} n_{i}}{\nu _{i}}}$

Ersetzt man im Ausdruck für das chemische Potential $\mathrm {d} n_{i}$ durch $\nu _{i}\cdot \mathrm {d} \xi$ und löst nach $\mathrm {d} G_{i}$ auf, erhält man:

$\mathrm {d} G_{i}=\nu _{i}\cdot \mu _{i}\cdot \mathrm {d} \xi$

Enthält ein Reaktionsgemisch insgesamt verschiedene Stoffe, gilt für die Änderung $\mathrm {d} G_{\mathrm {sys} }$ der freien Gesamtenthalpie $G_{\mathrm {sys} }$ des reagierenden Systems:

$\mathrm {d} G_{\mathrm {sys} }=\sum _{i=1}^{z}\mathrm {d} G_{i}=\sum _{i=1}^{z}(\nu _{i}\cdot \mu _{i}\cdot \mathrm {d} \xi )=\sum _{i=1}^{z}(\nu _{i}\cdot \mu _{i})\cdot \mathrm {d} \xi$

Dividieren durch $\mathrm {d} \xi$ ergibt:

$\left({\frac {\partial G_{\mathrm {sys} }}{\partial \xi }}\right)_{T,p}=\sum _{i=1}^{z}(\nu _{i}\cdot \mu _{i})$

Unter den gegebenen Reaktionsbedingungen für $T,p$ ist ${\frac {\partial G_{\mathrm {sys} }}{\partial \xi }}$ die Änderung der freien Systementhalpie $G_{\mathrm {sys} }$ pro Reaktionsumsatz.

Das chemische Potential $\mu _{i}$ eines Stoffes in einer Reaktionsmischung kann bezogen auf das chemische Potential $\mu _{i}^{\circ }$ des reinen Stoffes für den Referenzzustand ( $\circ$ ) ausgedrückt werden, der für das betrachtete Reaktionsszenario maßgeblich ist:

$\mu _{i}(a_{i})=\mu _{i}^{\circ }+R\cdot T\cdot \ln a_{i}$

Hierbei ist $a_{i}:=\exp \left({\frac {\mu _{i}-\mu _{i}^{\circ }}{RT}}\right)$ die relative chemische Aktivität mit der Gaskonstante und der absoluten Temperatur .

Die Kombination mit obigem Ausdruck für $\left(\partial G_{\mathrm {sys} }/{\partial \xi }\right)_{T,p}$ ergibt:

$\left({\frac {\partial G_{\mathrm {sys} }}{\partial \xi }}\right)_{T,p}=\sum _{i=1}^{z}(\nu _{i}\cdot \mu _{i}^{o}+\nu _{i}\cdot R\cdot T\cdot \ln a_{i})=\sum _{i=1}^{z}\nu _{i}\cdot \mu _{i}^{o}+R\cdot T\cdot \sum _{i=1}^{z}\nu _{i}\cdot \ln a_{i}$

Die Summe $\textstyle \sum _{{i}=1}^{z}{\nu _{i}}\cdot \mu _{i}^{\circ }=:\Delta _{R}G^{\circ }$ ist gleich der molaren freien Reaktionsenthalpie $\Delta _{R}G^{\circ }$ für den Referenzzustand. Man erhält:

$\left({\frac {\partial G_{\mathrm {sys} }}{\partial \xi }}\right)_{T,p}=\Delta _{R}G^{\circ }+R\cdot T\cdot \sum _{i=1}^{z}\nu _{i}\cdot \ln a_{i}$

Während $\Delta _{R}G^{\circ }$ konstant ist, solange Druck und Temperatur nicht verändert werden, hängt die Summe $\textstyle \sum _{{i}=1}^{z}\nu _{i}\cdot \ln a_{i}$ von den jeweils aktuellen relativen Aktivitäten $a_{i}$ ab. Durch Anwendung der einschlägigen Logarithmusregel lässt sich die Summe $\textstyle \sum _{{i}=1}^{z}\nu _{i}\cdot \ln a_{i}$ in den Logarithmus des Produkts $\textstyle \prod _{i=1}^{z}a_{i}^{{\nu }_{i}}$ umwandeln, welches als Reaktionsquotient $Q_{r}$ bezeichnet wird:

$\sum _{i=1}^{z}\nu _{i}\cdot \ln a_{i}=\ln \left(\prod _{i=1}^{z}a_{i}^{{\nu }_{i}}\right)=\ln Q_{r}$

Somit ergibt sich:

$\left({\frac {\partial G_{\mathrm {sys} }}{\partial \xi }}\right)_{T,p}=\Delta _{R}G^{\circ }+R\cdot T\cdot \ln Q_{r}$

Solange im Verlauf der betrachteten Reaktion die transienten relativen Aktivitäten der Edukte größer als die relativen Gleichgewichtsaktivitäten der Edukte sind, ist $Q_{r}$ kleiner als die Gleichgewichtskonstante , und es gilt:

$\Delta _{R}G^{\circ }+R\cdot T\cdot \ln Q_{r}<0$

Folglich nimmt $G_{\mathrm {sys} }$ mit Fortlaufen der Reaktion ab:

$\left({\frac {\partial G_{\mathrm {sys} }}{\partial \xi }}\right)_{T,p}<0$

Im chemischen Gleichgewicht nimmt die freie Gesamtenthalpie $G_{\mathrm {sys} }$ des reagierenden Systems den kleinstmöglichen erreichbaren Wert an. Im chemischen Gleichgewicht weist die Funktion $G_{\mathrm {sys} }(\xi )_{T,p}$ somit ein Minimum auf. Der partielle Differentialquotient $(\partial G_{\mathrm {sys} }/\partial \xi )_{T,p}$ muss demnach im chemischen Gleichgewicht gleich null sein:

$\left({\frac {\partial G_{\mathrm {sys} }}{\partial \xi }}\right)_{T,p}=\Delta _{R}G^{\circ }+R\cdot T\cdot \ln Q_{r}=0$

Der Reaktionsquotient $Q_{r}$ ist im chemischen Gleichgewicht allein durch die freie Reaktionsenthalpie im Referenzzustand $\Delta _{R}G^{\circ }$ gegeben und entspricht damit der Gleichgewichtskonstanten :

$\Delta _{R}G^{\circ }=-R\cdot T\cdot \ln Q_{r}=-R\cdot T\cdot \ln K$

Dieser Ausdruck stellt den Zusammenhang zwischen der molaren freien Reaktionsenthalpie $\Delta _{R}G^{\circ }$ und der stofflichen Zusammensetzung des Reaktionsgemisches im chemischen Gleichgewicht dar. Auflösen nach ergibt entsprechend:

$K=\exp {\bigg [}-{\frac {\Delta _{R}G^{\circ }}{R\cdot T}}{\bigg ]}=\prod _{i=1}^{z}a_{i}^{{\nu }_{i}}.$

Da von $\Delta _{R}G^{\circ }$ abhängt, hängt auch der Zahlenwert der Gleichgewichtskonstante vom jeweils angewendeten Referenzzustand ( $\circ$ ) ab.

Druck- und Temperaturabhängigkeit der Gleichgewichtskonstante

Da sich das Massenwirkungsgesetz auf ein unter den jeweiligen Reaktionsbedingungen anzuwendendes thermodynamisches Potential bezieht, ist die Gleichgewichtskonstante abhängig von den Zustandsgrößen, die die unabhängigen Zustandsvariablen des betreffenden thermodynamischen Potentials darstellen. Ist das relevante thermodynamische Potential die freie Enthalpie, ändert sich der Wert der Gleichgewichtskonstante, wenn die betrachtete Reaktion bei unverändertem Druck und einer veränderten konstanten Temperatur durchgeführt wird. Die Temperaturabhängigkeit der Gleichgewichtskonstante bei konstantem Druck lässt sich durch die van-’t-Hoff-Gleichung beschreiben beziehungsweise durch van-'t-Hoffsche Reaktionsisobaren darstellen. Ebenso ändert sich der Wert der Gleichgewichtskonstanten, wenn die betrachtete Reaktion bei unveränderter Temperatur und verändertem konstanten Druck durchgeführt wird. Zur Beschreibung der Druckabhängigkeit der Gleichgewichtskonstante bei konstanter Temperatur in kondensierten Phasen wird das molare Reaktonsvolumen $\Delta _{R}{\overline {V}}$ herangezogen:

$\left({\frac {\partial \ln K}{\partial p}}\right)_{T}=-{\frac {\Delta _{R}{\overline {V}}}{RT}}$

Die Druckabhängigkeit der Gleichgewichtskonstante ist bei Reaktionen, die in kondensierten Phasen stattfinden, jedoch typischerweise sehr schwach und wird häufig vernachlässigt. Ist das relevante thermodynamische Potential die freie Energie, wird die Temperaturabhängigkeit der Gleichgewichtskonstante bei konstantem Volumen durch die van-’t-Hoff’sche Reaktionsisochore beschrieben.

Massenwirkungsgesetz als Spezialfall in der Reaktionskinetik

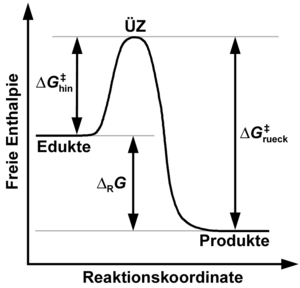
Profil der freien Enthalpie entlang der Reaktionstrajektorie einer Elementarreaktion. Um von den Ausgangsstoffen (Edukte) zum Übergangszustand (ÜZ) zu kommen, muss die freie Aktivierungsenergie der Hinreaktion $\Delta G_{\mathrm {hin} }^{\ddagger }$ aufgebracht werden. Durchläuft die Rückreaktion denselben Übergangszustand wie die Hinreaktion, ist die freie Aktivierungsenthalpie der Rückreaktion $\Delta G_{\text{rück}}^{\ddagger }$ gleich $\Delta G_{\mathrm {hin} }^{\ddagger }+\Delta _{\mathrm {R} }G$ (freie Reaktionsenthalpie).

Gemäß der Theorie des Übergangszustandes müssen im Verlauf elementarer Reaktionsereignisse Ausgangsstoffe und Produkte trennende Potentialbarrieren überwunden werden, die sich auf der makroskopischen Ebene am zweckmäßigsten durch das jeweils anzuwendende thermodynamische Potential beschreiben lassen. Reversible Reaktionen zeichnen sich dadurch aus, dass neben Hinreaktionen, die zur Bildung der Reaktionsprodukte aus den Ausgangsstoffen führen, auch Rückreaktionen, die zur Bildung der Ausgangsstoffe aus den Reaktionsprodukten führen, in nennenswertem Umfang stattfinden. Werden beispielsweise Druck und Temperatur konstant gehalten, repräsentiert die molare freie Aktivierungsenthalpie $\Delta {G^{\ddagger }}_{\mathrm {hin} }^{\circ }$ die Höhe der bei der Hinreaktion für die Umwandlung der Ausgangsstoffe in die Produkte zu überwindenden Potentialbarriere (bezogen auf den Referenzzustand). Entsprechend repräsentiert die molare freie Aktivierungsenthalpie $\Delta {G^{\ddagger }}_{\text{rück}}^{\circ }$ die Höhe der bei der Rückreaktion für die Umwandlung der Produkte in die Ausgangsstoffe zu überwindenden Potentialbarriere. Hin- und Rückreaktion können, müssen aber nicht entlang derselben Reaktionstrajektorie verlaufen. Sofern Hin- und Rückreaktion exakt entlang derselben Reaktionstrajektorie in jeweils entgegengesetzter Richtung ablaufen, gilt mit $\Delta _{\mathrm {R} }G^{\circ }$ als molarer freier Reaktionsenthalpie der Hinreaktion für $\Delta {G^{\ddagger }}_{\text{rück}}^{\circ }$ :

$\Delta _{\mathrm {R} }G^{\circ }=\Delta {G^{\ddagger }}_{\mathrm {hin} }^{\circ }-\Delta {G^{\ddagger }}_{\text{rück}}^{\circ }$

Die Kinetik einer betrachteten Reaktion wird durch ein Geschwindigkeitsgesetz beschrieben, in das das thermodynamische Aktivierungspotential mittels einer Geschwindigkeitskonststante eingeht. Die Geschwindigkeitskonstante der Hinreaktion ${\textstyle k_{\mathrm {hin} }}$ , die die Kinetik der Umwandlung der Ausgangsstoffe in die Produkte repräsentiert, hängt von $\Delta {G^{\ddagger }}_{\mathrm {hin} }^{\circ }$ wie folgt ab (siehe Abschnitt "Thermodynamische Formulierung" im Artikel "Theorie des Übergangszustandes")-->:

$k_{\mathrm {hin} }=\mathrm {Konstante} \cdot \exp {\bigg [}-{\frac {\Delta {G^{\ddagger }}_{\mathrm {hin} }^{\circ }}{RT}}{\Bigg ]}$

Entsprechend gilt für die Geschwindigkeitskonstante ${\textstyle k_{\text{rück}}}$ , die die Kinetik der Umwandlung der Produkte die Ausgangsstoffe durch die Rückreaktion repräsentiert:

$k_{\text{rück}}=\mathrm {Konstante} \cdot \exp {\bigg [}-{\frac {\Delta {G^{\ddagger }}_{\text{rück}}^{\circ }}{RT}}{\Bigg ]}$

Durch Anwendung des Ausdrucks $\Delta {G^{\ddagger }}_{\text{rück}}^{\circ }=\Delta {G^{\ddagger }}_{\mathrm {hin} }^{\circ }-\Delta _{\mathrm {R} }G^{\circ }$ lässt sich ${\textstyle k_{\text{rück}}}$ als Funktion von $\Delta _{\mathrm {R} }G^{\circ }$ und $\Delta {G^{\ddagger }}_{\mathrm {hin} }^{\circ }$ darstellen:

$k_{\text{rück}}=\mathrm {Konstante} \cdot \exp {\Bigg [}-{\frac {\Delta {G^{\ddagger }}_{\text{rück}}^{\circ }}{RT}}{\Bigg ]}={\rm {Konstante}}\cdot \exp {\Bigg [}-{\frac {\Delta {G^{\ddagger }}_{\mathrm {hin} }^{\circ }-\Delta _{\mathrm {R} }G^{\circ }}{RT}}{\Bigg ]}$

Für den Quotienten aus ${\textstyle k_{\mathrm {hin} }}$ und ${\textstyle k_{\text{rück}}}$ folgt:

${\frac {k_{\mathrm {hin} }}{k_{\text{rück}}}}=\exp {\Bigg [}-{\frac {\Delta {G^{\ddagger }}_{\mathrm {hin} }^{\circ }}{RT}}{\Bigg ]}\cdot \exp {\Bigg [}-{\frac {\Delta {G^{\ddagger }}_{\mathrm {hin} }^{\circ }-\Delta _{\mathrm {R} }G^{\circ }}{RT}}{\Bigg ]}^{-1}=\exp {\Bigg [}-{\frac {\Delta _{\mathrm {R} }G^{\circ }}{RT}}{\Bigg ]}=K$

Das Verhältnis ${\textstyle {\frac {k_{\mathrm {hin} }}{k_{\text{rück}}}}}$ ist somit gleich der Gleichgewichtskonstante ${\textstyle K}$ und wird durch die Referenz freie Reaktionsenthalpie $\Delta _{\mathrm {R} }G^{\circ }$ vorgegeben. Der Zusammenhang zwischen der Gleichgewichtskonstante und den Geschwindigkeitskonstanten der Hin- und Rückreaktion ist thermodynamisch begründet und gilt unabhängig von der Art und Weise, in der die die Reaktionskinetik beschreibenden Geschwindigkeitsgesetze formuliert werden.

Entsprechen für eine reversible Reaktion

$|\nu _{\mathrm {A} }|\,\mathrm {A} +|\nu _{\mathrm {B} }|\,\mathrm {B} \rightleftharpoons \nu _{\mathrm {C} }\,\mathrm {C} +\nu _{\mathrm {D} }\,\mathrm {D}$

lassen sich mit $r_{\mathrm {hin} }$ sowie $r_{\text{rück}}$ als Reaktionsgeschwindigkeiten der Hin- und Rückreaktion folgende Geschwindigkeitsgesetze formulieren (siehe auch Ratengleichung):

$r_{\mathrm {hin} }=k_{\mathrm {hin} }\cdot a_{\text{A}}}^{|\nu _{\text{A}}|}\cdot {a_{\text{B}}}^{|\nu _{\text{B}}|$

$r_{\text{rück}}=k_{\text{rück}}\cdot a_{\text{C}}}^{|\nu _{\text{C}}|}\cdot {a_{\text{D}}}^{|\nu _{\text{D}}|$

Teilt man den Ausdruck für $r_{\text{rück}}$ durch den Ausdruck für $r_{\mathrm {hin} }$ , erhält man:

${\frac {r_{\text{rück}}}{r_{\mathrm {hin} }}}={\frac {{k_{\text{rück}}\cdot a_{\text{C}}}^{|\nu _{\text{C}}|}\cdot {a_{\text{D}}}^{|\nu _{\text{D}}|}}{{k_{\text{hin}}\cdot a_{\text{A}}}^{|\nu _{\text{A}}|}\cdot {a_{\text{B}}}^{|\nu _{\text{B}}|}}}$

Mit $K={\frac {k_{\mathrm {hin} }}{k_{\text{rück}}}}$ sowie $K={\frac {{a_{\text{C}}}^{|\nu _{\text{C}}|}\cdot {a_{\text{D}}}^{|\nu _{\text{D}}|}}{{a_{\text{A}}}^{|\nu _{\text{A}}|}\cdot {a_{\text{B}}}^{|\nu _{\text{B}}|}}}$ erhält man:

${\frac {r_{\text{rück}}}{r_{\mathrm {hin} }}}={\frac {1}{K}}\cdot K=1$

Daraus folgt, dass im chemischen Gleichgewicht die Geschwindigkeit der Hinreaktion $r_{\mathrm {hin} }$ gleich der Geschwindigkeit der Rückreaktion $r_{\text{rück}}$ sein muss:

$r_{\text{hin}}=r_{\text{rück}}$

Aufstellung des Massenwirkungsgesetzes mit Stoffmengenkonzentrationen

Die relativen Aktivitäten $a_{i}={\frac {c_{i}}{c^{\circ }}}\gamma _{i}$ sind relativ zum Referenzzustand (mit Referenzkonzentration $c^{\circ }$ ), wobei der Aktivitätskoeffizient $\gamma_i$ für wechselwirkende Systeme ungleich eins ist. Durch Einsetzen der relativen Aktivitäten erhält man

$K=\prod _{i=1}^{z}a_{i}^{{\nu }_{i}}=\prod _{i=1}^{z}\left({\frac {c_{i}}{c^{\circ }}}\gamma _{i}\right)^{{\nu }_{i}}.$

Unter Vernachlässigung der Teilchenwechselwirkungen – d.h. durch Fordern, dass die Aktivitätskoeffizienten $\gamma _{i}\approx 1$ – erhält man

$K\approx \prod _{i=1}^{z}\left({\frac {c_{i}}{c^{\circ }}}\right)^{{\nu }_{i}},$

was für verdünnte Lösungen häufig eine gute Näherung ist. Teilweise werden die Referenzkonzentrationen zusätzlich in die Definition einer neuen Gleichgewichtskonstante einbezogen:

$K_{c}:=K\prod _{i=1}^{z}\left(c^{\circ }\right)^{{\nu }_{i}}\approx \prod _{i=1}^{z}c_{i}^{{\nu }_{i}}.$

Statt thermodynamisch korrekt mit den Aktivitäten der an der betrachteten Reaktion beteiligten Stoffe kann somit das Massenwirkungsgesetz für Reaktionen in verdünnter Lösung häufig näherungsweise unter Verwendung der Stoffmengenkonzentrationen der beteiligten Stoffe aufgestellt werden. Bei stärker konzentrierten Lösungen können jedoch die Werte der Aktivitätskoeffizienten stark von 1 abweichen, so dass diese Näherung mit Vorsicht zu gebrauchen ist. Die mit Stoffmengenkonzentrationen berechneten Gleichgewichtskonstanten werden zur Unterscheidung von mit Aktivitäten berechneten Gleichgewichtskonstanten mit K_c bezeichnet, wobei der tiefgestellte Index c für Stoffmengenkonzentration steht. Das Massenwirkungsgesetz wird zum Beispiel für die Reaktion

$|\nu _{\mathrm {A} }|\,\mathrm {A} +|\nu _{\mathrm {B} }|\,\mathrm {B} \rightleftharpoons \nu _{\mathrm {C} }\,\mathrm {C} +\nu _{\mathrm {D} }\,\mathrm {D}$

unter Verwendung der Stoffmengenkonzentrationen c(A), c(B), c(C) und c(D) der Ausgangsstoffe A und B sowie der Produkte C und D wie folgt formuliert:

$K_{c}={\frac {c(\mathrm {C} )^{\nu _{\mathrm {C} }}\cdot c(\mathrm {D} )^{\nu _{\mathrm {D} }}}{c(\mathrm {A} )^{|\nu _{\mathrm {A} }|}\cdot c(\mathrm {B} )^{|\nu _{\mathrm {B} }|}}}$

Da die stöchiometrischen Zahlen $\nu _{\mathrm {A} }$ und $\nu _{\mathrm {B} }$ der Ausgangsstoffe A und B als Exponenten von deren Stoffmengenkonzentrationen c(A) und c(B) definitionsgemäß ein negatives Vorzeichen besitzen, stehen die Produktterme $c(\mathrm {A} )^{|\nu _{\mathrm {A} }|}$ und $c(\mathrm {B} )^{|\nu _{\mathrm {B} }|}$ im Nenner des Ausdrucks für $K_{c}$ .

Eine mittels der Stoffmengenkonzentrationen erhaltene Gleichgewichtskonstante $K_{c}$ hat in der Regel einen anderen Zahlenwert als die entsprechende mittels der Aktivitäten erhaltene Gleichgewichtskonstante. Weiterhin kann $K_{c}$ eine Dimension und damit auch eine Einheit besitzen. $\nu _{\mathrm {ges} }$ sei die Summe aller stöchiometrischer Zahlen $\nu _{i}$ der beteiligten Stoffe ${\textstyle i}$ einer Reaktion mit ${\textstyle z}$ beteiligten Stoffen:

$\nu _{\mathrm {ges} }=\sum _{i=1}^{z}\nu _{i}$

${\textstyle L}$ ist das Dimensionssymbol für Länge, ${\textstyle N}$ das Dimensionssymbol für die Stoffmenge. Die Dimension der Stoffmengenkonzentration ist $N/L^{3}$ und die Dimension von $K_{c}$ demzufolge $(N/L^{3})^{\nu _{\mathrm {ges} }}$ . Lediglich wenn $\nu _{\mathrm {ges} }=0$ ist, ist $K_{c}$ dimensionslos. Betrachtet man beispielsweise die Synthese von Kaliumhexacyanidoferrat(II) gemäß

$\mathrm {Fe^{2+}+6\ CN^{-}\rightleftharpoons [Fe(CN)_{6}]^{4-}}$ ,

ergibt sich für $K_{c}$ :

$K_{c}=\mathrm {\frac {c([Fe(CN)_{6}]^{4-})}{c(Fe^{2+})\cdot c^{6}(CN^{-})}}$

In diesem Beispiel ist $\nu _{\mathrm {ges} }=-1-6+1=-6$ und die Dimension von $K_{c}$ gleich $(N\cdot L^{-3})^{-6}=N^{-6}\cdot L^{18}$ . Die Einheit von $K_{c}$ ist demnach $\mathrm {m} ^{18}\cdot \mathrm {Mol} ^{-6}$ .

Um eine dimensionslose Form der stoffmengenkonzentrationsbasierten Gleichgewichtskonstante $K_{c}$ zu erhalten, kann $K_{c}$ durch die Einheitskonzentration $1\;\mathrm {Mol} \cdot \mathrm {m} ^{-3}$ potenziert mit $\nu _{\mathrm {ges} }$ dividiert werden.

Aufstellung des Massenwirkungsgesetzes für homogene Gasgleichgewichte

Für Gasphasenreaktionen wird das Massenwirkungsgesetz häufig mit den Partialdrücken ${\textstyle p_{i}}$ der beteiligten Stoffe ${\textstyle i}$ aufgestellt. Als Symbol für mit Partialdrücken erhaltene Gleichgewichtskonstanten wird ${\textstyle K_{p}}$ verwendet. Bei homogenen Gasgleichgewichten mit ${\textstyle z}$ beteiligten Komponenten nimmt das Massenwirkungsgesetz entsprechend folgende Form an:

$K_{p}=\prod _{i=1}^{z}p_{i}^{{\nu }_{i}}$

Bei der Bildung von Iodwasserstoff aus elementarem Wasserstoff und Iod

$\mathrm {{H_{2}}_{(g)}+{I_{2}}_{(g)}\rightleftharpoons 2\ {HI}_{(g)}}$

stellt sich das Gleichgewicht

$K_{p}={\frac {p^{2}\mathrm {(HI)} }{p\mathrm {(H_{2})} \cdot p\mathrm {(I_{2})} }}$

ein. ${\textstyle K_{p}}$ und ${\textstyle K_{c}}$ beziehungsweise die Partialdrücke ${\textstyle p_{i}}$ und die Stoffmengenkonzentrationen ${\textstyle c_{i}}$ lassen sich über die Zustandsgleichung für ideale Gase miteinander verknüpfen:

$p_{i}V=n_{i}RT$ $\Leftrightarrow p_{i}={\frac {n_{i}}{V}}RT=c_{i}RT$

Für die Gleichgewichtskonstante ${\textstyle K_{p}}$ bei der Bildung von Iodwasserstoff ergibt sich:

$K_{p}={\frac {[c\mathrm {(HI)} RT]^{2}}{c\mathrm {(H_{2})} RT\cdot \ c\mathrm {(I_{2})} RT}}={\frac {c^{2}\mathrm {(HI)} }{c\mathrm {(H_{2})} \cdot c\mathrm {(I_{2})} }}=K_{c}$

Ist in einem Gasphasengleichgewicht die Teilchenanzahl der Produkte gleich der Teilchenanzahl der Edukte, so kürzt sich ${\textstyle RT}$ im mit Stoffmengenkonzentrationen formulierten Massenwirkungsgesetz heraus. Betrachtet man jedoch die Reaktion von Schwefeldioxid und Sauerstoff zu Schwefeltrioxid

$\mathrm {2\ {SO_{2}}_{(g)}+{O_{2}}_{(g)}\rightleftharpoons 2\ {SO_{3}}_{(g)}}$ mit $K_{p}={\frac {p^{2}\mathrm {\mathrm {(SO_{3})} } }{p^{2}\mathrm {(SO_{2})} \cdot p\mathrm {(O_{2})} }}$

und ersetzt die Drücke durch Stoffmengenkonzentrationen, ergibt sich:

$K_{p}={\frac {[c\mathrm {(SO_{3})} RT]^{2}}{[c\mathrm {(SO_{2})} RT]^{2}\cdot c\mathrm {(O_{2})} RT}}={\frac {c^{2}\mathrm {\mathrm {(SO_{3})} } }{c^{2}\mathrm {(SO_{2})} \cdot c\mathrm {(O_{2})} }}\cdot {\frac {1}{RT}}=K_{c}\cdot {\frac {1}{RT}}$

Die Teilchenzahl vermindert sich bei der Reaktion und ein Faktor ${\textstyle 1/RT}$ verbleibt im mit Stoffmengenkonzentrationen formulierten Massenwirkungsgesetz.

Betrachtet man die Bildung von Ammoniak im Haber-Bosch-Verfahren gemäß

$\mathrm {{3\ H_{2}}_{(g)}+{N_{2}}_{(g)}\rightleftharpoons {2\ NH_{3}}_{(g)}}$ ,

ergibt sich:

$K_{p}={\frac {p^{2}\mathrm {(NH_{3})} }{p\mathrm {(N_{2})} \cdot p^{3}\mathrm {(H_{2})} }}$

Die Umrechnung von $K_{p}$ in $K_{c}$ erfolgt gemäß:

$K_{p}={\frac {[c\mathrm {(NH_{3})} RT]^{2}}{c\mathrm {(N_{2})} RT\cdot [c\mathrm {(H_{2})} RT]^{3}}}={\frac {c^{2}\mathrm {(NH_{3})} }{c\mathrm {(N_{2})} \cdot c^{3}\mathrm {(H_{2})} }}\cdot {\frac {1}{(RT)^{2}}}=K_{c}\cdot {\frac {1}{(RT)^{2}}}$

Allgemein lässt sich also das Massenwirkungsgesetz eines Gasphasengleichgewichts ausdrücken als:

$K_{p}=K_{c}\cdot {(RT)^{\nu _{\mathrm {ges} }}}$

Dabei ist ${\textstyle \nu _{\mathrm {ges} }=\textstyle \sum _{{i}=1}^{z}{\nu _{i}}\displaystyle }$ die Summe der stöchiometrische Zahlen der betrachteten Reaktion. Im Fall der Bildung von HI aus den Elementen ist $\nu _{\mathrm {ges} }=-1-1+2=0$ . Beim Haber-Bosch-Verfahren ist $\nu _{\mathrm {ges} }=-3-1+2=-2$ .

Alternativ ist es oft zweckmäßig, die Zusammensetzung der Gasphase über Molenbrüche (Stoffmengenanteile) ${\textstyle \chi _{i}}$ anzugeben. In diesem Fall wird eine auf die Stoffmengenanteile bezogene Gleichgewichtskonstante $K_{x}$ erhalten:

$K_{x}=\prod _{i=1}^{z}x_{i}^{{\nu }_{i}}$ mit $x_{i}={\frac {p_{i}}{p}}$

Allgemein gilt hier:

$K_{x}=K_{c}\cdot {\left({\dfrac {RT}{p}}\right)^{\nu _{\mathrm {ges} }}}$

Anwendungen des Massenwirkungsgesetzes

Für eine Vielzahl von Spezialfällen definiert das Massenwirkungsgesetzes – teilweise in vereinfachter Form – Gleichgewichtskonstanten für spezifische Reaktionsszenarien. So beschreiben Assoziations- und Dissoziationskonstanten das Gleichgewicht für Assoziations- und Dissoziationsprozesse. Das Löslichkeitsprodukt definiert die Gleichgewichtslöslichkeit von Salzen in Wasser. Komplexbildungskonstanten quantifizieren die Stabilität von Komplexverbindungen. Ionenprodukte werden durch Vereinfachung des Massenwirkungsgesetzes für elektrolytische Dissoziationsprozesse erhalten. Die quantitative thermodynamische Beschreibung der Säure-Base-Chemie durch Säurekonstanten und Basenkonstanten basiert auf dem Massenwirkungsgesetz. Die Protolyse von Essigsäure in wässeriger Lösung wird beispielsweise durch folgende stöchiometrische Reaktionsgleichung beschrieben:

$\mathrm {CH_{3}COOH_{(aq)}+H_{2}O_{(aq)}\rightleftharpoons H_{3}O_{(aq)}^{+}+CH_{3}COO_{(aq)}^{-}}$

Die Säurekonstante $K_{\mathrm {s} }$ von Essigsäure ergibt sich gemäß:

$K_{\mathrm {s} }={\frac {c(\mathrm {H} _{3}\mathrm {O} ^{+})\cdot c(\mathrm {CH_{3}COO} ^{-})}{c(\mathrm {CH_{3}COOH} )}}=K_{c}\cdot c(\mathrm {H_{2}O} )$

Literatur

Peter W. Atkins, Julio de Paula: Physikalische Chemie. Aus dem Englischen von Michael Bär, Anna Schleitzer und Carsten Heinisch. 5. Auflage. Wiley-VCH, Weinheim 2013, ISBN 978-3-527-33247-2.
Andreas Heintz: Thermodynamik der Mischungen – Mischphasen, Grenzflächen, Reaktionen, Elektrochemie, äußere Kraftfelder. Springer-Verlag, Berlin/Heidelberg 2017, ISBN 978-3-662-49923-8, doi:10.1007/978-3-662-49924-5.
Charles E. Mortimer, Ulrich Müller: Chemie – Das Basiswissen der Chemie. 13. Auflage. Georg Thieme Verlag, Stuttgart 2019, ISBN 978-3-132-42274-2.

Basierend auf einem Artikel in:

Wikipedia.de