Wirkungsquerschnitt
Der Wirkungsquerschnitt
(sigma) ist in der Molekül-,
Atom-,
Kern-
und Teilchenphysik
ein Maß für die Wahrscheinlichkeit,
dass zwischen einer einfallenden Wellenstrahlung
oder einem einfallenden Teilchen
(„Projektil“) und einem anderen Teilchen (Streukörper oder Target) ein
bestimmter Prozess wie z.B. Absorption,
Streuung
oder eine Reaktion
stattfindet.
Der Wirkungsquerschnitt hat die Dimension Fläche. Er wird meist in folgenden Einheiten angegeben:
- in der Kern- und Teilchenphysik in Barn (1 b = 10−28 m2 = 10−4 pm2 = 100 fm2)
- in der Atom- und Molekülphysik in 10−22 m2 = 1 Mb = 10−4 nm2 = 100 pm2.
Die Vorstellung vom Wirkungsquerschnitt als einer jedem Targetteilchen zugeordneten Trefferfläche bietet ein anschauliches Maß für die „Stärke“ des jeweils betrachteten Vorgangs: Einem häufig eintretenden Vorgang entspricht ein großer Wirkungsquerschnitt, einem selten eintretenden ein kleiner Wirkungsquerschnitt. Mit anschaulichen Vorstellungen über Größe, Form und Lage des Targetteilchens stimmt diese Trefferfläche allerdings im Allgemeinen nicht überein.
Der Wirkungsquerschnitt hängt ab von dem jeweils interessierenden Vorgang, von Art und kinetischer Energie des einfallenden Teilchens oder Quants und von der Art des getroffenen Teilchens (z. B. Atom, Atomkern). Die letztgenannte Abhängigkeit bedeutet, dass Wirkungsquerschnitte Materialeigenschaften sind. Beispielsweise sind zur Berechnung von Kernreaktoren oder Kernfusionsreaktoren umfangreiche Kerndatenbibliotheken erforderlich, die die Wirkungsquerschnitte der verschiedenen Materialien für einfallende Neutronen verschiedener Energien für verschiedene mögliche Streuprozesse und Kernreaktionen enthalten.
Insbesondere bei Kernreaktionen wird der Wirkungsquerschnitt, betrachtet als Funktion der Energie des einfallenden Teilchens/Quants, manchmal auch als Anregungsfunktion bezeichnet.
Spezielle Bezeichnungen
Je nach Art des betrachteten Vorgangs werden verschiedene Bezeichnungen für den Wirkungsquerschnitt verwendet:
- Absorptionsquerschnitt für jede Absorption des einfallenden Teilchens
- Streuquerschnitt für Streuung, also Ablenkung des einfallenden Teilchens
- Extinktionsquerschnitt für Schwächung oder Energieentnahme, Summe von Streu- und Absorptionsquerschnitt
- Einfangquerschnitt für eine bestimmte Absorption, nämlich den Neutroneneinfang
(die (n,
)-Kernreaktion)
- Reaktionsquerschnitt für die chemische Reaktion, die durch den Stoß zweier Atome oder Moleküle ausgelöst wird
- Elastischer Wirkungsquerschnitt (oft auch nur „elastischer Querschnitt“) für elastischen Stoß, also einen Stoß, bei dem die gesamte kinetische Energie erhalten bleibt
- Inelastischer Wirkungsquerschnitt („inelastischer Querschnitt“) für inelastischen Stoß, also einen Stoß, bei dem die kinetische Energie in andere Energieformen übergeht, z.B. wird ein Teilchen angeregt (d.h. in einen Zustand höherer Energie versetzt) oder es werden neue Teilchen erzeugt
- Ionisationsquerschnitt für die Ionisation des getroffenen Atoms
- Spaltquerschnitt für die induzierte Kernspaltung
- Strahlungsdruckquerschnitt für Strahlungsdruck.
Definition
Bei einem Experiment mit gleichmäßiger Bestrahlung des Targets wird dem Zielteilchen (Targetteilchen) eine Fläche σ als gedachte „Zielscheibe“ zugeordnet. Ihre Größe wird so gewählt, dass die Zahl der beobachteten Reaktionen ("Wechselwirkungen") genau durch die Anzahl der – punktförmig, also ausdehnungslos gedachten – Projektilteilchen angegeben wird, die durch diese Fläche hindurchfliegen. Diese Fläche ist der Wirkungsquerschnitt des betreffenden Targets für die betreffende Wechselwirkung bei der betreffenden Energie der Projektilteilchen.
Die Wahrscheinlichkeit ,
dass ein einfallendes Teilchen mit einem Targetteilchen wechselwirkt,
errechnet sich aus
Darin ist
die bestrahlte Targetfläche und
die Anzahl der darin enthaltenen Targetteilchen;
auch wird
vorausgesetzt, weil sich die Targetteilchen sonst gegenseitig abschatten.
Wenn insgesamt
Projektilteilchen einlaufen und jedes von ihnen mit der Wahrscheinlichkeit
eine Reaktion verursacht, dann ist die Gesamtzahl der Reaktionen gegeben
durch:
Zusammen:
Zur experimentellen Bestimmung eines Wirkungsquerschnitts wird
durch geeignete Detektoren
gemessen, während
,
und
aus Aufbau und Durchführung des Experiments bekannt sind.
In der theoretischen Herleitung (z.B. in der quantenmechanischen
Streutheorie) wird die
Formel häufig noch durch die Zeit dividiert, also die Reaktionsrate
gebildet:
mit
- der Teilchenstromdichte
der Projektilteilchen und
- der Luminosität
der Kombination von Target und Teilchenstrahl.
Abschwächung des einfallenden Teilchenstrahls im dicken Target
Für eine infinitesimal
dünne Targetschicht der Dicke
erhält man aus der obigen Gleichung, wenn man für „Teilchen pro Fläche“ das
Produkt „Teilchendichte
mal Dicke
“
einsetzt:
.
Hierbei ist
die Teilchendichte des Targetmaterials, also die Anzahl der Targetteilchen pro
Volumeneinheit:
mit
der Avogadrokonstante
der Massendichte und
der Molaren Masse.
Löst man obige Gleichung nach
auf und setzt dies gleich
,
erhält man die Differentialgleichung
Die Lösung hierfür ist
Interpretation: die wechselwirkenden Projektilteilchen
sind nicht mehr Teil des einfallenden Strahls mit der Teilchenanzahl
,
da sie (bei Reaktion) absorbiert oder (bei Streuung) aus ihrer ursprünglichen
Bahn abgelenkt worden sind. D.h., nach dem Durchlaufen einer Targetschicht
der Dicke x sind nur noch
Teilchen im Strahl vorhanden.
Betrachtet man die Wechselwirkungen in einem bestimmten Volumen, so ist ,
wenn
die Länge dieses Volumens ist. Setzt man dieses ein, kann man zur Berechnung des
Wirkungsquerschnitt die Gleichung umstellen:
Offenbar gilt auch
wobei
die mittlere
freie Weglänge ist, nach der die Intensität des einfallenden Strahls auf
ihres ursprünglichen Wertes abgefallen ist.
Sofern mehr als eine Art von Vorgang möglich ist, bezieht sich
in dieser Gleichung auf alle zusammen, ist also der totale
Wirkungsquerschnitt (siehe unten).
Totaler Wirkungsquerschnitt
Die Bezeichnung „totaler Wirkungsquerschnitt“ wird in zwei Bedeutungen verwendet:
- Manchmal ist damit der Wirkungsquerschnitt für das Eintreten irgendeines von mehreren möglichen, einander ausschließenden Vorgängen gemeint, z. B. Absorption oder Streuung des einfallenden Teilchens. Dieser totale Wirkungsquerschnitt ist die Summe der Einzel-Wirkungsquerschnitte. Er wird beispielsweise dann benötigt, wenn es nur um die Abschwächung des einfallenden Teilchenstroms geht.
- Manchmal wird „Totaler Wirkungsquerschnitt“ auch nur im Sinne des oben
definierten Wirkungsquerschnitts für einen bestimmten Vorgang verwendet, um
ihn vom differenziellen Wirkungsquerschnitt
(s. unten) zu unterscheiden; eine bessere Bezeichnung ist in diesem Fall „Integraler Wirkungsquerschnitt“. Es gilt:
Differentieller Wirkungsquerschnitt
Wenn durch die Reaktion zwischen der einfallenden Primärstrahlung und dem
Target eine Sekundärstrahlung
entsteht (gestreute Primärstrahlung oder eine andere Art von Strahlung), wird
deren Intensitätsverteilung über die Raumrichtungen
beschrieben durch den differenziellen Wirkungsquerschnitt
Darin ist
die Stromdichte der in Richtung Ω auslaufenden Sekundärstrahlung bei Anwesenheit eines einzigen Targetteilchens (
, vgl. Definition), gegeben in Teilchen pro Raumwinkel-Einheit und Zeiteinheit
die Stromdichte der (parallel einlaufenden) Primärstrahlung in Teilchen pro Flächen-Einheit und Zeiteinheit.
Daher hat
die Dimension Fläche pro Raumwinkel und als Maßeinheit z.B. Millibarn pro Steradiant. (Physikalisch
gesehen ist der Raumwinkel dimensionslos und der differenzielle
Wirkungsquerschnitt
daher von derselben Dimension Fläche wie der Wirkungsquerschnitt
selbst.)
Um die richtige Trefferfläche für die Erzeugung der Sekundärstrahlung in
Richtung
zu erhalten, betrachtet man die gesamte Sekundärstrahlung in ein kleines
Raumwinkelelement
hinein. Sie ist in erster Näherung gegeben durch
Der Ausdruck auf der linken Seite entspricht genau der Reaktionsrate wie oben
erwähnt (bei NT = 1), man denke sich etwa ein Experiment mit
einem Detektor von genau der Größe ,
der auf jedes ankommende Sekundärteilchen anspricht. Daher steht auf der rechten
Seite vor der einlaufenden Stromdichte
mit dem Faktor
genau die Trefferfläche (richtig mit Dimension Fläche), die zu den in diesem Experiment beobachteten Reaktionen gehört.
Das Integral des differenziellen Wirkungsquerschnitts über alle Richtungen ist der totale (oder integrale) Wirkungsquerschnitt für den beobachteten Typ der Reaktion:
Der differenzielle Wirkungsquerschnitt hängt ab
- wie der Wirkungsquerschnitt selbst: von der Art der Reaktion (Art des Targets, Art und Energie der Teilchen der Primär- und der Sekundärstahlung)
- zusätzlich von der Richtung
, die durch zwei Winkel angegeben werden kann. Meist interessiert nur der Ablenkwinkel relativ zur Richtung des Primärstrahls; dann heißt der differenzielle Wirkungsquerschnitt auch kurz Winkelverteilung.
Mit der Bezeichnung „Differenzieller Wirkungsquerschnitt“ ohne weiteren
Zusatz ist fast immer
gemeint. Weitere differenzielle Wirkungsquerschnitt sind:
Sekundärenergieverteilung
Seltener benötigt wird der nach der Energie
des Sekundärteilchens, also des gestreuten Teilchens oder Reaktionsproduktes,
abgeleitete Wirkungsquerschnitt
,
der die Energieverteilung der Sekundärteilchen beschreibt. Er hängt ab von der
Primär- und der Sekundärenergie.
Doppelt differenzieller Wirkungsquerschnitt
Bei komplexen Vorgängen wie etwa dem Eindringen (Transport) schneller
Neutronen in dicke Materieschichten, wo ein Neutron an verschiedenen
Streuprozessen und Kernreaktionen nacheinander teilnehmen kann, wird auch der
doppelt differenzielle Wirkungsquerschnitt
betrachtet, da er die detaillierteste physikalische Beschreibung erlaubt.
Geometrischer Wirkungsquerschnitt
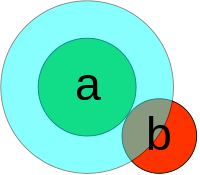
(zum 1. Beispiel):
wenn der Mittelpunkt von Teilchen b in den blauen Kreis eindringt, kommt es zur Kollision mit Teilchen a.
Die Fläche des blauen Kreises ist somit der geometrische Wirkungsquerschnitt, sein Radius ist die Summe der Teilchenradien.
In der klassischen Mechanik fliegen alle Teilchen auf wohldefinierten Trajektorien. Für Reaktionen, die eine Berührung von Projektil- und Targetteilchen voraussetzen, wird der Begriff geometrischer Wirkungsquerschnitt benutzt, denn hier haben nicht nur die Größe des Wirkungsquerschnitt als Trefferfläche, sondern auch deren Form und Lage (relativ zum Targetteilchen) eine einfache geometrische Bedeutung: alle Teilchen, die auf ihrer Trajektorie durch diese Fläche fliegen, lösen die betrachtete Reaktion aus, alle anderen nicht.
- Beispiel Stoß zweier Kugeln (Radien
und
, vgl. Abbildung): Eine Berührung mit der Targetkugel a findet genau für die Projektilkugeln b statt, deren Mittelpunkt am Mittelpunkt der Targetkugel nicht weiter entfernt vorbeifliegen würde als durch die Summe ihrer beider Radien angegeben ist. Die Trefferfläche ist für den Mittelpunkt der bewegten Kugel also eine Kreisscheibe um den Mittelpunkt der ruhenden Kugel mit Radius
. Der (totale) Wirkungsquerschnitt ist die Fläche dieses Kreises:
- Beispiel Fußball (Radius
) und Torwand (Radius des Lochs
), Flugrichtung senkrecht zur Wand. Gefragt sei der geometrische Wirkungsquerschnitt für die (Zuschauer-)Reaktion TOOR!!, also für freies Hindurchfliegen: Falls
gilt, ist
. Im Fall
passt der Ball zwar hindurch, doch darf die Trajektorie des Ballmittelpunkts den Lochmittelpunkt höchstens um den Abstand
verfehlen. Die Trefferfläche (für den Mittelpunkt des Balls) liegt als Kreisscheibe mit Radius
um den Mittelpunkt des Lochs. Der geometrische Wirkungsquerschnitt ist
-
.
Beide Beispiele zeigen, dass man nicht einmal den geometrischen Wirkungsquerschnitt mit der Größe eines der beteiligten Körper identifizieren darf (außer wenn das Projektil einschließlich der Reichweite der Kraft als punktförmig angesehen wird). Das zweite zeigt zudem, wie groß der Anwendungsbereich des Begriffs Wirkungsquerschnitt sein kann.
Bei Wellenphänomenen ist die geometrische Interpretation nicht möglich. Auch in der Quantenmechanik können prinzipiell keine deterministischen Aussagen über einzelne Projektil- oder Targetteilchen gemacht werden.
Makroskopischer und temperaturabhängiger Wirkungsquerschnitt
In der Physik der Kernreaktoren wird neben dem oben definierten
mikroskopischen (d.h. auf 1 Targetteilchen, meist 1 Atom
bezogenen) Wirkungsquerschnitt auch der makroskopische, auf
1 cm3 Material bezogene Wirkungsquerschnitt mit dem
Formelzeichen
(großes Sigma) verwendet. Er ergibt sich aus dem mikroskopischen
Wirkungsquerschnitt durch Multiplikation mit der Atomzahldichte,
also der Zahl der jeweiligen Atome pro cm3. Die übliche Einheit
des makroskopischen Wirkungsquerschnitts ist cm2/cm3 =
1/cm. In diesem Anwendungsbereich sind im Allgemeinen die Energien der beiden
Reaktionspartner nicht einheitlich festgelegt, sondern variieren im Rahmen
bestimmter Häufigkeitsverteilungen, und die interessierende Größe ist der
Durchschnittswert des makroskopischen Wirkungsquerschnitts. Dieser kann dann
z.B. temperaturabhängig sein.
Wirkungsquerschnitt und Fermis Goldene Regel
Fermis
Goldene Regel besagt, dass für die Reaktionsrate
(Anzahl von Reaktionen pro Zeit) gilt:
mit
dem reduzierten Planckschen Wirkungsquantum
dem Übergangsmatrixelement bzw. der Wahrscheinlichkeitsamplitude (in der Bornschen Näherung gegeben durch den Formfaktor des Potentials der Wechselwirkung)
dem Phasenraumfaktor.
Da die Reaktionsrate außerdem direkt proportional zum (differentiellen) Wirkungsquerschnitt ist
-
(vgl. oben:
als Luminosität des Teilchenstrahls),
gilt folglich:
Siehe auch


© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 03.08. 2025