Welle

Eine Welle ist eine sich räumlich ausbreitende periodische (Schwingung) oder einmalige (Störung) Veränderung des Gleichgewichtszustands eines Systems bezüglich mindestens einer orts- und zeitabhängigen physikalischen Größe. Unterschieden werden mechanische Wellen, die stets an ein Medium gebunden sind, und Wellen, die sich auch im Vakuum ausbreiten können (beispielsweise elektromagnetische Wellen, Materiewellen oder Gravitationswellen). In Medien wird die Ausbreitung einer örtlichen Störung durch die Kopplung benachbarter Oszillatoren (schwingfähige physikalische Größen) vermittelt. Eine Welle transportiert Energie, jedoch keine Materie, d.h. die benachbarten Oszillatoren transportieren die Störung durch den Raum, ohne sich selbst im zeitlichen Mittel fortzubewegen. Direkt wahrnehmbare Wellen sind zum Beispiel Schallwellen, Wasserwellen und Licht.

Kreisförmige Wellen im Wasser

Wellentypen

Wellenarten:
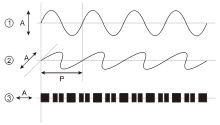
1. und 2. Transversalwelle
3. Longitudinalwelle

Wellen werden in mehrere Kategorien unterteilt: die „klassischen“ Longitudinal- und Transversalwellen (von denen auch Mischformen wie Torsionswellen auftreten können) sowie Materiewellen (nach der Theorie von Louis de Broglie hat ein sich bewegendes Teilchen auch eine Wellenlänge, die bei entsprechendem Versuchsaufbau auch nachgewiesen werden kann) und Wahrscheinlichkeitswellen, die im Rahmen der Quantenphysik die Zustände von physikalischen Systemen beschreiben. Gravitationswellen stauchen und strecken die Raumzeit quer zu ihrer Ausbreitungsrichtung.

Mechanische Longitudinalwellen können sich in jedem Medium, ob fest, flüssig oder gasförmig ausbreiten, wogegen sich mechanische, reine Transversalwellen nur in Festkörpern ausbreiten können. Elektromagnetische Wellen in verlustfreien Medien (z.B. im Vakuum) sind transversal.

Longitudinalwellen

→ Hauptartikel: Longitudinalwelle

Wellen, die parallel zur Ausbreitungsrichtung schwingen, werden als Longitudinal- oder Längswelle bezeichnet. Ein wichtiges Beispiel ist der Schall, der sich in Gasen und Flüssigkeiten immer als Longitudinalwelle ausbreitet.

Mechanische Longitudinalwellen sind Druckwellen. Das bedeutet, dass sich in einem Medium Zonen mit Überdruck bzw. Druckspannung (bzw. Unterdruck oder Zugspannung) in der Ausbreitungsrichtung fortpflanzen bzw. verschieben oder ausbreiten. Die einzelnen Teilchen im Ausbreitungsmedium, Atome oder Moleküle, schwingen hierbei in Richtung der Ausbreitung um den Betrag der Amplitude hin und her. Nach dem Durchlauf der Schwingung bewegen sich die Teilchen wieder an ihre Ruhestellung, die Gleichgewichtslage, zurück.

Die Leistung einer Longitudinalwelle ist proportional zum Quadrat der Amplitude oder der Druckspannung, siehe auch Schalldruck und Schallschnelle. Longitudinalwellen haben im gleichen festen Medium eine höhere Geschwindigkeit als Transversalwellen des gleichen Typs bei ansonsten gleichen Parametern.

Transversalwelle

→ Hauptartikel: Transversalwelle

Wellen, die senkrecht zur Ausbreitungsrichtung schwingen, werden als Transversal-, Quer-, Schub- oder Scherwellen bezeichnet. Nur Transversalwellen können polarisiert sein.

Beispiele sind elektromagnetische Wellen, Gravitationswellen, Biegewellen und Plasmawellen.

Auch Schallwellen im Festkörper und seismische Wellen können sich bei geeigneter Materialbeschaffenheit als Transversalwelle fortpflanzen.

Wasserwellen sind als Oberflächenwellen in der Regel eine Mischform aus Longitudinal- und Transversalwellen, können aber als stehende Welle (Seiche) auch als reine Transversalwelle auftreten. Sie bilden entweder Schwere- oder Kapillarwellen oder eine Übergangsform zwischen beiden.

Mathematische Beschreibung

Bezeichnung

Symbol

Beziehungen

Amplitude

$\mathbf {A} _{0}$

$\mathbf {A} _{0}\perp \mathbf {k}$	Transversalwelle
$\mathbf {A} _{0}\\|\mathbf {k}$	Longitudinalwelle

Wellenvektor

$\mathbf {k}$

Ausbreitungsrichtung

Kreiswellenzahl

$k\,$

$k=|\mathbf {k} |$

Wellenlänge

$\mathbf {\lambda }$

$\mathbf {\lambda } =2\mathbf {\pi } /k$

Kreisfrequenz

$\mathbf {\omega }$

$\mathbf {\omega } \left(\mathbf {k} \right)$ Dispersionsrelation

Frequenz

$f\,$

$f=\mathbf {\omega } /2\mathbf {\pi }$

Phasengeschwindigkeit

$c\,$

$c=\mathbf {\omega } /k=\mathbf {\lambda } f$

Gruppengeschwindigkeit

$v_{G}\,$

$v_{G}=d\mathbf {\omega } /dk$

Phase

$\varphi$

$\varphi =\mathbf {k} \cdot \mathbf {r} -\omega t$

Zur mathematischen Beschreibung von Wellen sind mehrere Größen nötig. Dazu zählen Amplitude, Phase und Ausbreitungs- oder Phasengeschwindigkeit. Die nebenstehende Tabelle gibt einen Überblick über die Größen, die zur vollständigen Beschreibung nötig sind.

Wellenfunktion

Mathematisch spricht man von einer Welle, wenn die Wellenfunktion $\mathbf {A} (\mathbf {r} ,t)$ , also die die Welle mathematisch beschreibende Gleichung, eine Lösung einer Wellengleichung ist. Diese Funktionen hängen im Allgemeinen von Ort $\mathbf {r}$ und Zeit $t\,$ ab.

Dabei gibt $\mathbf {A}$ die Auslenkung am Ort $\mathbf {r}$ zur Zeit $t\,$ an. Funktionen dieses Typs entsprechen der Vorstellung, dass Wellen räumlich ausgedehnte Schwingungen sind. Eine allgemeine Funktion für jede Art von Welle anzugeben, ist dabei nicht ohne weiteres möglich. Häufig werden daher sehr einfache Lösungen der Wellengleichung herangezogen und die reale Welle als eine Überlagerung von vielen dieser Lösungen angesehen. Die gebräuchlichsten Elementarlösungen sind die Ebene Welle und die Kugelwelle.

Amplitude

Die Amplitude $\mathbf {A} _{0}$ ist die maximale mögliche Auslenkung der Welle. Sie ist bei Wellen – im Gegensatz zu Schwingungen – eine vektorielle Größe, da neben der Stärke der Auslenkung auch deren Richtung entscheidend ist. Ist die Ausbreitungsrichtung parallel zur Amplitude, handelt es sich um eine Longitudinalwelle, ist sie senkrecht, um eine Transversalwelle. In beiden Fällen ist die Intensität der Welle proportional zum Quadrat der Amplitude.

Phase

Phasenverschobene Sinusschwingungen gleicher Frequenz

Sinusschwingungen unterschiedlicher Frequenz

Die Phase einer Welle gibt an, in welchem Abschnitt innerhalb einer Periode sich die Welle zu einem Referenzzeitpunkt und -ort befindet. Sie legt also fest, wie groß die Auslenkung ist. Im Beispiel einer ebenen Welle ist $\varphi =\mathbf {k} \cdot \mathbf {r} -\omega t$ die Phase zum Zeitpunkt $t\,$ am Ort $\mathbf {r}$ . Die Phase hängt also von den zwei Parametern Wellenvektor $\mathbf {k}$ und Kreisfrequenz $\omega$ ab.

Beispiele

Die mathematische Formulierung für eine harmonische (auch: homogene, monochromatische) ebene Welle im dreidimensionalen Raum ist in komplexer Schreibweise:

$\mathbf {A} (\mathbf {r} ,t)=\operatorname {Re} \left(\mathbf {A} _{0}e^{i\left(\mathbf {k} \cdot \mathbf {r} -\omega t\right)}\right)=\operatorname {Re} (\mathbf {A} _{0})\cos(\mathbf {k} \cdot \mathbf {r} -\omega t)-\operatorname {Im} (\mathbf {A} _{0})\sin(\mathbf {k} \cdot \mathbf {r} -\omega t).$

Eine Kugelwelle lässt sich mit folgender Gleichung beschreiben:

$\mathbf {A} (r,t)=\operatorname {Re} \left({\frac {\mathbf {A} _{0}}{r}}e^{i(kr-\omega t)}\right)={\frac {\operatorname {Re} (\mathbf {A} _{0})}{r}}\cos(kr-\omega t)-{\frac {\operatorname {Im} (\mathbf {A} _{0})}{r}}\sin(kr-\omega t).$

Erzeugung von Wellen

Konzentrische Wellenringe aus einem reinen Sinus nach außen abnehmender Amplitude (3D)

Ausbreitung einer Welle

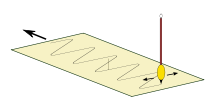
Quellen für Wellen können pulsförmige Anregungen, Vibrationen oder periodische Schwingungen sein. Periodische mechanische und elektromagnetische Wellen können durch periodische Schwingungen erzeugt werden. Ein einfaches Beispiel ist ein schwingendes Pendel: An einem solchen Pendel befindet sich zum Beispiel ein Stift, unter dem ein Blatt Papier mit konstanter Geschwindigkeit hergezogen wird. Der am Pendel befestigte Stift beschreibt nun auf dem Papierstreifen, der das Ausbreitungsmedium darstellt, eine sinusförmige Welle. Bei diesem Beispiel ist die Wellenlänge abhängig von der Geschwindigkeit, mit der der Papierstreifen bewegt wird. Die Amplitude der Welle wird durch den maximalen Pendelausschlag bestimmt.

Eine elektromagnetische Welle kann durch eine Antenne erzeugt werden, die an einen elektrischen Schwingungsgenerator angeschlossen ist. Als Schwingungsgenerator kann ein sogenannter Schwingkreis verwendet werden, bei dem der elektrische Strom zwischen einer Spule und einem Kondensator hin und her fließt. Die elektromagnetische Gesamtenergie wird im Schwingkreis periodisch von elektrischer Energie (vermittelt durch das elektrische Feld im Kondensator) in magnetische Energie (vermittelt durch das magnetische Feld der Spule) umgewandelt. Geschieht dies mit einer geeigneten Frequenz für die verwendete Antenne, so wird ein Teil der Energie in Form einer elektromagnetischen Welle effizient von der Antenne in den Raum abgestrahlt. Dieser Effekt ist vor allem in der drahtlosen Kommunikation von besonderer Bedeutung.

Überlagerung von Wellen

Interferenz zweier Wellen

Eine stehende Welle

Schwebung

Gauß’sches Wellenpaket

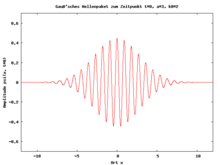
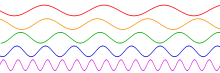
In der Natur vorkommende Wellen sind in den seltensten Fällen reine monochromatische Wellen, sondern eine Überlagerung aus vielen Wellen unterschiedlicher Wellenlängen. Die Überlagerung erfolgt dabei durch das Superpositionsprinzip, was mathematisch bedeutet, dass alle Wellenfunktionen der einzelnen Wellen addiert werden. Die Anteile der Wellenlängen werden als Spektrum bezeichnet. Beispiele:

Sonnenlicht ist eine Überlagerung aus elektromagnetischen Wellen. Das Spektrum umfasst einen Wellenlängenbereich von Infrarot über sichtbares Licht bis Ultraviolett. Derartige Spektren bezeichnet man auch als kontinuierlich.
Ein Musikton eines Instrumentes setzt sich zusammen aus einem Grundton und mehreren Oberschwingungen. Die unterschiedlichen Anteile an Oberschwingungen sind der Grund, warum eine Posaune anders klingt als eine Flöte. Ein solches Spektrum heißt diskret, da es sich nur aus einzelnen, klar abgetrennten Wellenlängen zusammensetzt.

Dabei können verschiedene Effekte auftreten:

Interferenz − Überlagert man Wellen, so kann es zu einer konstruktiven Verstärkung, aber auch zu einer teilweisen oder gar totalen Auslöschung der Welle (wenn beide Wellenlängen und Frequenzen gleich sind und die Wellen genau gegenläufig schwingen) kommen. Dieses Phänomen spielt im Alltag zum Beispiel bei dem unerwünschten Mehrwegempfang eine Rolle – an einem Ort treffen auf verschiedenen Wegen Wellen eines Senders ein und können sich dort unter Umständen gegenseitig auslöschen.
Stehende Welle − Bei Überlagerung zweier sich gegenläufig ausbreitender Wellen derselben Frequenz und Amplitude kommt es zur Ausbildung von stehenden Wellen. Diese breiten sich nicht aus, sondern bilden räumlich konstante Schwingungsmuster: An den sogenannten Bewegungsbäuchen schwingen sie mit der verdoppelten Amplitude und der ursprünglichen Frequenz, an den dazwischenliegenden Bewegungsknoten ist die Amplitude zu allen Zeiten Null. Diese Erscheinung ist ein Sonderfall der Interferenz. Sie tritt insbesondere vor einer reflektierenden Wand auf oder auch zwischen zwei passend abgestimmten Wänden, die gemeinsam einen Resonator bilden.
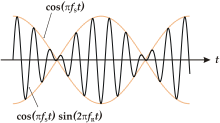
Schwebung − Eine Überlagerung zweier Wellen von benachbarter Frequenz führt zu einer Schwebung. Die Amplitude einer solchen Welle nimmt periodisch zu und ab – je näher die Frequenzen beieinander liegen, desto (zeitlich) langsamer geschieht dieser Vorgang. Dieser Effekt wird beispielsweise beim Stimmen von Musikinstrumenten ausgenutzt – die Schwebungsfrequenz wird dabei zu nahe Null einjustiert. Typisch sind auch die Schwebungen des Leslie-Lautsprechers. Dessen langsame Schwebungen empfindet der Mensch als angenehm.
Wellenpaket − Die Überlagerung von Wellen mit allen Frequenzen aus einem Frequenzband erzeugt ein Wellenpaket. Hierbei zeigt die Einhüllende der Welle nur einen einzelnen Berg, vor und hinter diesem ist die Amplitude vernachlässigbar. Da die Phasengeschwindigkeit einer Welle in Wellenleitern und dispersiven Medien frequenzabhängig ist, zerfließen Wellenpakete mit fortschreitender Zeit. Bei der Nachrichtenübermittlung mittels Wellen muss die resultierende Verbreiterung von Wellenpaketen berücksichtigt werden.

Basierend auf einem Artikel in:

Wikipedia.de