Widerstandsmessgerät

Ein Widerstandsmessgerät ist ein Messgerät, mit dem der elektrische Widerstand eines elektrischen Bauelementes oder einer elektrischen Schaltung gemessen werden kann. Üblicherweise ist es ausgelegt speziell zur Messung des ohmschen Widerstands. Mit Geräten für diese Messaufgabe befasst sich dieser Artikel im Wesentlichen.

In diesem Fall baut die Messung darauf auf, dass am Messobjekt das ohmsche Gesetz gilt. Entweder wird eine im Messgerät vorhandene, auf einen festgelegten Wert eingestellte elektrische Spannung an das Messobjekt angelegt, und die sich einstellende Stromstärke wird zum Maß für dessen Widerstand; oder ein im Messgerät bereitgestellter, auf einen festgelegten Wert eingestellter elektrischer Strom wird durch das Messobjekt geführt, und der sich einstellende Spannungsabfall wird zum Maß für dessen Widerstand.

Wegen der eingebauten Spannungsquelle oder Stromquelle darf ein Widerstandsmessgerät nicht an ein Messobjekt angeschlossen werden, das seinerseits eine Spannungs- oder Stromquelle enthält.

Durchgangsprüfer zum Erkennen einer elektrischen Verbindung sind keine Mess-, sondern Prüfgeräte oder Indikatoren.

Die Bezeichnung eines Widerstandsmessgerätes als Ohmmeter ist überholt und kollidiert außerdem mit der gleichlautenden Einheit Ohmmeter. Mit Ohm wird eine definierte, nicht messbare Maßeinheit bezeichnet und nicht die physikalische Größe, die tatsächlich gemessen wird.

Fallunterscheidung

Der Widerstand eines elektrisch leitenden Bauteils bei Gleichspannung resultiert aus dessen geometrischer Form und einer Materialeigenschaft. Er führt zu einem ohmschen Widerstand oder Gleichstromwiderstand. Fallweise ist der Widerstand von der Stromstärke abhängig, und es ergibt sich statt des ohmschen ein nichtlinearer Widerstand. Dann ist die Widerstandsmessung unter Betriebsbedingungen nur über Strom- und Spannungsmessgeräte möglich, siehe nachfolgend. Dann kann auch die Kenntnis des differenziellen Widerstands wichtig sein; zu dessen Messung siehe weiter unten.

Bei Betrieb an Wechselspannung tragen zusätzlich Induktivität und Kapazität des Bauteils einen Wechselstromanteil (Blindwiderstand) zum Widerstand bei. Gleichstrom- und Wechselstromanteil werden zusammengefasst zur Impedanz oder zum komplexen Widerstand; zu dessen Messung siehe unter Wechselspannungsbrücke.

Häufig sind bei ohmschen Widerständen sich langsam einstellende kleine Änderungen zu messen, ohne dass der Widerstand selber genau bekannt sein muss; zu deren Messung siehe unter Wheatstone-Brücke im Ausschlagsverfahren.

Bevorzugte Messverfahren

Strom- und Spannungsmessung

Digital-Messgeräte

In einem Digitalmultimeter ist zur Widerstandsmessung eine Konstantstromquelle eingebaut, justiert auf einen glatten Zehnerpotenzwert in mA oder μA, so dass der Zahlenwert der gemessenen Spannung unmittelbar den Zahlenwert des Widerstands ergibt, ohne die Stromstärke zu messen. Nur die Komma-Stellung und das Einheitenzeichen (Ω, kΩ) werden passend zum Messbereich im Gerät umgeschaltet. Die Fehlergrenzen liegen je nach Herstellerangaben bei ≤ 1 ;% vom Messwert + 1 ‰ vom Endwert.

Üblicherweise besitzen Digitalmultimeter eine automatische Bereichswahl und schalten die Stromstärke der Konstantstromquelle selbsttätig auf den passenden Messbereich um. Zur Verwendung als Durchgangsprüfer besitzen sie oft einen zuschaltbaren Signalton.

Analog-Messgeräte

Die unterste von ∞ bis 0 reichende Skale dient der Widerstandsmessung

Analoge Widerstandsmessgeräte bestehen aus einem Zeigermessgerät mit Drehspulmesswerk, einem einstellbaren Vorwiderstand und einer Hilfsspannungsquelle (Batterie); sie besitzen eine stark nichtlineare Skale, auf der der Widerstandswert unmittelbar in Ohm oder Kiloohm abgelesen werden kann.

Wegen des großen, über alle denkbaren Messwerte reichenden Messbereichs 0 … ∞ ist nur im mittleren Bereich der Skale ein einigermaßen genaues Ablesen möglich. Manche Widerstandsmesser haben einen umschaltbaren Messbereich, um im mittleren Skalenbereich jeweils andere Werte bevorzugt ablesen zu können.

Wegen der Speisung aus einer nicht stabilisierten Spannungsquelle (Batterie mit alterungsbedingt absinkender Spannung) ist vor der Messung das Gerät zu justieren. Dazu wird bei Kurzschluss zwischen den Messklemmen ein von außen zugängliches Potentiometer (Teil des Vorwiderstandes) so eingestellt, dass = 0 angezeigt wird. Damit ändert sich jedoch prinzipbedingt auch die Skalierung. Auch im mittleren Teil der Skale liegen daher die typischen Fehlergrenzen bei etwa 10 % vom Messwert.

Aufgrund der Nachteile wie der komplizierteren Anwendung, den größeren Messfehlern, höhere mechanische Empfindlichkeit sind analoge Widerstandsmessgeräte im praktischen Laborbetrieb fast vollständig durch digitale Multimeter zur Widerstandsmessung verdrängt worden.

Messschaltung mit Strom- und Spannungsmessgerät

Über Strom- und Spannungsmessgeräte

Je nach Umständen wird auf das Widerstandsmessgerät mit seiner eingebauten Spannungs- oder Stromquelle verzichtet, wenn eine externe Speisung vorhanden ist. Dann müssen am Messobjekt sowohl der Spannungsabfall als auch die Stromstärke gemessen werden. Bei Gleichspannungsspeisung wird aus diesen beiden Werten der ohmsche Widerstand R=U/I berechnet. Bei Wechselstromspeisung ergibt sich der Scheinwiderstand. Bei einstellbarer Speisung kann der Arbeitspunkt, bei dem gemessen werden soll, selbst gewählt werden.

Dieses Verfahren ist prinzipiell nicht frei von systematischen Messabweichungen. Die Rückwirkungsabweichungen (Schaltungseinflussfehler) durch den Innenwiderstand R_I des Strommessgerätes oder R_U des Spannungsmessgerätes lassen sich aber durch einen aufwändigeren Ansatz ausschließen:

In der oberen Schaltung (stromrichtige Schaltung) ist die gemessene Spannung um den Spannungsabfall am Strommesser größer als die Spannung am Widerstand,

mit $U_I=I\cdot R_I$ .

In der unteren Schaltung (spannungsrichtige Schaltung) ist die gemessene Stromstärke um die Stromaufnahme des Spannungsmessers größer als die Stromstärke durch den Widerstand,

mit

Brückenschaltung

Hier handelt es sich um ein Präzisionsverfahren mit Spannungskompensation, in dem die am Messobjekt abfallende Spannung verglichen wird mit einer weiteren, an einem bekannten Widerstand abfallenden Spannung. Zur Messung wird eine der Spannungen an die andere angeglichen; siehe hierzu Wheatstonesche Messbrücke im Abgleichverfahren.

Messung kleiner Widerstände

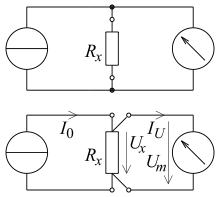
Widerstandsmessung mit Konstantstromquelle und Spannungsmessgerät,
oben Anschluss in Zweileiterschaltung,
unten Anschluss in Vierleiterschaltung

Bei der Messung kleiner Widerstände $R_{x}$ (Richtwert $R_{x}$ < 1 Ω) machen sich Übergangswiderstände $R_{Kl}$ in den Anschlussklemmen als Messabweichung bemerkbar; siehe hierzu Messwiderstand. Dieser Einfluss lässt sich vermeiden durch Anschluss in Vierleitertechnik (Kelvinanschluss) mit Klemmen für die Stromeinspeisung und getrennt davon herausgeführten und getrennt angeschlossenen Klemmen für die Spannungsmessung. Unter folgenden Bedingungen sind systematische Messabweichungen ausgeschlossen:

Wenn die Stromstärke durch den Spannungsmesser vernachlässigbar klein ist

$I_U\ll I_0$

und der Spannungsverlust in den Klemmen für die Messleitungen vernachlässigbar klein ist,

$I_U\ R_{Kl} \ll I_0\ R_x$

ergibt sich der Widerstandswert aus

$R_x = U_m / I_0\ .$

Bei Speisung aus einer Konstantstromquelle hat der Spannungsabfall an den Stromklemmen keinen Einfluss auf $I_{0}$ und tritt als Ursache für eine Messabweichung nicht in Erscheinung.

Zu einem älteren analogen Messverfahren siehe unter Thomson-Brücke.

Ein digitales Messverfahren zur Messung kleiner Widerstände arbeitet folgendermaßen:

Digitale Spannungsmesser bilden eine Anzeige durch Vergleich der zu messenden Spannung mit einer eingebauten Referenzspannung $U_{ref}$ ; siehe Digitale Messtechnik. Z.B. beim Zweirampenverfahren entsteht bei einer zu messenden Spannung $U_{m}$ eine Anzeige $N_{m}$ gemäß

Schaltung zur digitalen Messung kleiner Widerstände; ADU: Spannungsmessgerät

$U_m= - U_{ref} \frac{N_m}{N_i}$

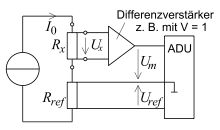
Darin ist $N_{i}$ eine Geräte-Konstante.

Auf die genaue Kenntnis von $I_{0}$ kann verzichtet werden, wenn die Referenzspannung ebenfalls aus $I_{0}$ gebildet wird mit einem in Vierleitertechnik eingebauten Referenzwiderstand, siehe Schaltung.

$U_{ref}= - I_0 R_{ref}$

$U_m =V\,U_x$

$U_m = -U_{ref} \frac{N_m}{N_i} =I_0 R_{ref} \frac{N_m}{N_i}$

$R_x =\frac{U_x}{I_0} = \frac{U_m}{VI_0} =R_{ref} \frac{N_m}{VN_i}$

Die Anzeige $N_{m}$ ist proportional zu $R_{x}$ . Das Verfahren ist realisiert mit einem Messbereich 200 μΩ bei einer kleinsten Schrittweite 1 nΩ.

Messung großer Widerstände

Bei der Messung großer Widerstände $R_{x}$ (Richtwert $R_{x}$ > 20 MΩ) wird die geringe Größe des noch fließenden Stromes bei den üblichen kleinen Messspannungen zum Problem. Die Messspannung muss erhöht werden, was jedoch oft nur bei Isolationsmessgeräten möglich ist. Diese bieten umschaltbare Messspannungen ab etwa 100 V. Die Spannung ist begrenzt durch die Durchschlagfestigkeit oder vorgegeben durch Prüfvorschriften.

Der Hauptbedarf der Messung sehr hoher Widerstände (Giga- bis Teraohm-Bereich) liegt bei der Messung an Isolierstoffen (Kunststoffe, Kabel, Folien usw.). An diesen Körpern ist zu unterscheiden zwischen

dem Oberflächenwiderstand mit Stromfluss längs der Oberfläche und
dem Volumenwiderstand oder Durchgangswiderstand mit Stromfluss quer zur Oberfläche, also durch den Körper hindurch.

Wegen der sehr kleinen, durch äußere Störungen und Leckströme leicht verfälschbaren Stromstärken (bis < 1 pA) ist eine Schutzschirm-Technik (Guard-Technik) erforderlich, die eine dritte Verbindung zwischen Messobjekt und Messgerät erfordert. Dieser zusätzliche Anschluss hat Masse- bzw. Erd-Potential und schafft ein durchgängiges Bezugspotential der Abschirmung (z.B. der Guard-Ringe), ohne in die Strommessung einbezogen zu sein. Solche Guard-Ringe umgeben zum Beispiel die Anschlussbuchsen für das Messobjekt oder auch die Anschlussbeine des zur Stromverstärkung verwendeten Operationsverstärkers auf der Leiterplatte des Messgerätes.

Widerstands-Messzelle mit drei Elektroden

Messanordnung mit Spannungs-, Strom- und Guard-Anschluss zur Messung eines Durchgangswiderstands

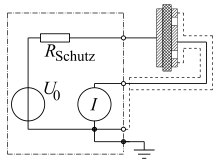
Zur Messung des Isolationswiderstandes eines ebenen Messobjektes arbeitet man mit

einer kreisförmigen Innenelektrode,
einer diese umgebende Ringelektrode und
einer gegenüberliegenden Gegenelektrode.

Zur Messung des Volumenwiderstandes (→ Abbildung) wird die durch den Körper über die Innenelektrode zum Bezugspotential fließende Stromstärke gemessen. Die Gegenelektrode liegt an der Prüfspannung. Die Ringelektrode wird in diesem Beispiel an Bezugspotential (Guard) angeschlossen; daher besteht keine Spannung zur Innenelektrode, und es kann kein Oberflächenstrom fließen. In diesem Zusammenhang spricht man auch von einem Schutzringkondensator.

Zur Messung des Oberflächenwiderstands wird die entlang der Oberfläche vom Ring zur Innenelektrode fließende Stromstärke gemessen. Die Ringelektrode liegt dazu an der Prüfspannung. Die Gegenelektrode wird an Bezugspotential bzw. Masse angeschlossen; daher besteht keine Spannung zur Innenelektrode, und es kann kein Strom durch das Volumen fließen.

Der Schutzwiderstand macht die Anordnung kurzschlussfest.

Das Verfahren ist geeignet bis zu einem Messbereich 100 GΩ bei einer relativen Fehlergrenze von 1 % und einem Messbereich 100 TΩ bei einer Fehlergrenze von 10 %.

Messung differentieller Widerstände

In einem rechtwinkligen Diagramm mit linear geteilten Achsen, in dem über aufgetragen wird, ergibt sich bei einem Bauteil mit ohmschem Verhalten eine Gerade durch den Nullpunkt; deren Anstieg ist anschaulich der Widerstand. Manche Bauteile, insbesondere Halbleiterbauteile, aber auch Glühlampen, haben ein nichtlineares Verhalten: Statt einer Geraden ergibt sich eine gekrümmte Kennlinie. Das Verhältnis $U/I$ ist hier bei jedem Strom bzw. jeder Spannung ein anderes; es ist kein Bauteil-Kennzeichen mehr. Man betrachtet die Spannungsänderung, die sich aufgrund einer kleinen Stromstärkeänderung ergibt, und bezeichnet deren Verhältnis als differentiellen Widerstand :

$r =\frac{\mathrm dU}{\mathrm dI}$

Er ist in dem genannten Diagramm der Anstieg der Kennlinie (Tangente an der Kennlinie) in einem bestimmten Punkt (dem Arbeitspunkt des Bauteils oder einer anderen festzulegenden Stromstärke).

Der differentielle Widerstand ist eine wichtige Kenngröße von Halbleiterdioden (Gleichrichter, Zener-Dioden, Leuchtdioden, Laserdioden).

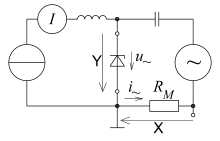
Messanordnung zur Messung eines differentiellen Widerstands mittels eines Oszilloskops;
als Messobjekt ist eine Zener-Diode eingezeichnet

Die rechts stehende Schaltung arbeitet zusammen mit einem Oszilloskop in XY-Betrieb und eignet sich zur direkten Bestimmung des differentiellen Widerstandes, ohne vorher eine Kennlinie aufnehmen zu müssen:
Mit einer Konstantstromquelle wird am Messobjekt ein Arbeitspunkt eingestellt. Diesem Gleichstrom wird aus einer Wechselspannungsquelle ein kleiner Wechselstrom überlagert. Der Kondensator sperrt Gleichstrom ab, lässt aber Wechselstrom durch. Die Spule sperrt Wechselstrom ab, besitzt für Gleichstrom aber nur etwa den Drahtwiderstand. Die Wechselspannung über dem Messobjekt wird zur Y-Ablenkung des Oszilloskops verwendet, die Wechselspannung über R_M als Maß für den Wechselstrom zur X-Ablenkung. Man sieht auf dem Bildschirm ein fast geradliniges kleines Teilstück der Kennlinie um den Arbeitspunkt herum. Aus dem Anstieg $\mathrm dY/\mathrm dX$ bestimmt sich der differentielle Widerstand $\mathrm dU/\mathrm dI$ .

Basierend auf einem Artikel in:

Wikipedia.de