Wheatstonesche Messbrücke

Die Wheatstonesche Messbrücke (kurz: Wheatstone-Brücke) ist eine Messeinrichtung zur Messung von

elektrischen Widerständen ohmscher Art (Gleichstromwiderstand),
kleinen ohmschen Widerstandsänderungen.

Sie ist aufgebaut aus vier Widerständen, die zu einem geschlossenen Ring oder Quadrat zusammengeschaltet sind, mit einer Spannungsquelle in der einen Diagonalen und einem Spannungsmessgerät in der anderen.

Sie wurde 1833 von Samuel Hunter Christie erfunden, jedoch nach dem britischen Physiker Sir Charles Wheatstone [ˈwiːtstən] benannt, der ihre Bedeutung erkannte und ihre Verbreitung förderte.

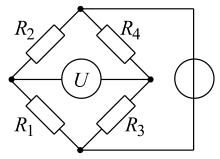
Grundaufbau der Wheatstone-Brücke

Beschreibung

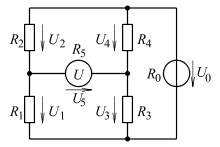
Grundaufbau der Wheatstone-Brücke, umgezeichnet

Eine grafisch andere Anordnung zeigt deutlicher, dass jeweils zwei Widerstände einen Spannungsteiler bilden; zwei Spannungsteiler liegen zueinander parallel. Das Spannungsmessgerät stellt zwischen diesen eine Querbeziehung her, die der Schaltung den Namen Brückenschaltung gibt. Die unmittelbar gemessene Größe der Anordnung ist der Spannungsunterschied zwischen den Spannungsteilern, auch Diagonalspannung oder Brückenquerspannung genannt.

Die ursprüngliche Wheatstone-Brücke diente zur Messung von Widerstandswerten durch Anwendung des Abgleichverfahrens. Zunächst müssen die drei bekannten Widerstände solange verändert werden, bis die Diagonalspannung null beträgt. Anschließend lässt sich aus deren Widerstandswerten der vierte, der unbekannte Wert berechnen. Durch die Verfügbarkeit günstiger elektronischer Messgeräte (die mit anderen Verfahren arbeiten; siehe Widerstandsmessgerät) wird diese Messmethode nur noch selten eingesetzt. Eine Ausnahme bilden hier Präzisionsmessungen.

Eine häufig ebenfalls als Wheatstone-Brücke (alternativ Ausschlag-Widerstandsmessbrücke) bezeichnete Methode ist die Abwandlung zum Ausschlagverfahren, bei dem selbst kleine Abweichungen des Widerstands ermittelt werden können, die bei der Messung des gesamten Widerstands kaum auflösbar wären.

Erläuterndes Beispiel: Eine Brücke mit einem Temperatur-Messwiderstand in einem der Spannungsteiler befindet sich bei einer Referenztemperatur im abgeglichenen Zustand. Ändert sich die Temperatur am Messwiderstand, dann ändert sich die Diagonalspannung näherungsweise proportional zur Temperaturänderung. Das Ausschlagverfahren nimmt in der modernen Messtechnik einen festen Platz ein.

Grundlage

An den zwei parallelen Spannungsteilern wird die Spannung über einem beliebigen Widerstand (z.B. $R_{1}$ ) verglichen mit der entsprechenden Spannung im Parallelzweig (dann über $R_{3}$ ). Falls diese Spannungen gleich groß (aber ungleich null) sind, nennt man die Brücke abgeglichen. Solange im Brückenquerzweig ein vernachlässigbar kleiner Strom fließt (bei Abgleich gilt das immer, sonst wenn $R_5\gg R_1\;,\ R_2\;,\ R_3\;,\ R_4$ ), sind die Spannungsteiler unbelastet, und es gilt:

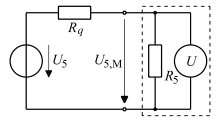
${\begin{aligned}U_{1}&=U_{0}{\frac {R_{1}}{R_{1}+R_{2}}}\\U_{3}&=U_{0}{\frac {R_{3}}{R_{3}+R_{4}}}\\U_{5}&=U_{1}-U_{3}=U_{0}\left({\frac {R_{1}}{R_{1}+R_{2}}}-{\frac {R_{3}}{R_{3}+R_{4}}}\right)\\&=U_{0}{\frac {R_{1}R_{4}-R_{3}R_{2}}{(R_{1}+R_{2})(R_{3}+R_{4})}}\end{aligned}}$

Ersatzschaltbild für die Ausgangsspannung

Bei der Messung dieser Spannung ist zu beachten, dass sie mit einem beträchtlichen Quellenwiderstand $R_{q}$ aufgrund der Spannungsteiler verbunden ist. Bei idealer Quelle der Speisespannung $U_{0}$ (mit $R_{0}=0$ zwischen dem oberen Anschluss von $R_{4}$ und dem unteren Anschluss von $R_{3}$ ) ist unmittelbar an der Schaltung ersichtlich:

$R_{q}=(R_{1}\parallel R_{2})+(R_{3}\parallel R_{4})={\frac {R_{1}\cdot R_{2}}{R_{1}+R_{2}}}+{\frac {R_{3}\cdot R_{4}}{R_{3}+R_{4}}}$

Für eine symmetrische Brücke mit $R_{1}=R_{2}=R_{3}=R_{4}=R$ gilt damit $R_{q}=R$ .

Zusammen mit einem nicht idealen Spannungsmessgerät mit einem Innenwiderstand $R_5<\infty$ kann das zu einer beträchtlichen Messabweichung führen, da die gemessene Spannung $U_{{5{,}{\mathrm M}}}$ gegenüber der Leerlaufspannung $U_{5}$ um den Faktor $R_{5}/(R_{5}+R_{q})\!$ kleiner ist; siehe reale Spannungsquelle.

Abgleichverfahren

Brücke zur Widerstandsmessung

Man definiert den abgeglichenen Zustand durch $U_{5}=0$ ; dann ist

$R_{1}\,R_{4}=R_{2}\,R_{3}$

oder

${\frac {R_{1}}{R_{2}}}={\frac {R_{3}}{R_{4}}}$

Diese Gleichung besagt: Wenn drei Widerstände bekannt sind, kann man einen vierten berechnen. Das liefert eine Messmethode zur Widerstandsmessung, die man auch Nullabgleichsmethode der Wheatstone-Brücke nennt.

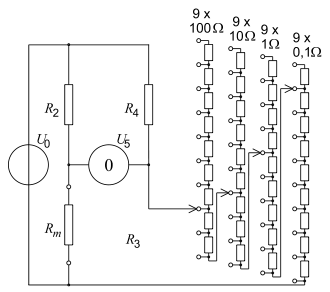
Messung mit Widerstandsdekaden

Wenn der zu messende Widerstand $R_{m}$ auf der Position von $R_{1}$ liegt, dann gilt

$R_{m}={\frac {R_{2}}{R_{4}}}\ \cdot R_{3}$

und man stellt bei der gezeigten Schaltung mit $R_{3}$ einen vierstelligen Wert ein und mit R_2:R_4 den Messbereich, sinnvollerweise einen Zehnerpotenzfaktor, z.B. 1:1 oder 1:10 oder 100:1. Der Einsatzbereich deckt etwa die Spanne $R_m=1\;\Omega\;\dots\;1\;\mathrm M\Omega$ ab.

Die letzte Gleichung ist unabhängig von der Speisespannung $U_{0}$ . Dennoch ist zu beachten:

$U_{0}$ soll so groß sein, dass bei fast abgeglichener Brücke eine Verstellung von $R_{3}$ um einen Schritt auf der niederwertigsten Stelle noch eine erkennbare Änderung der Brückenquerspannung $U_{5}$ hervorruft.
$U_{0}$ soll so klein sein, dass die unvermeidliche Erwärmung der Widerstände diese nicht erkennbar verändert.

Die Brücke kann auch mit Tonfrequenz statt mit Gleichspannung betrieben und als Indikator ein Kopfhörer verwendet werden, der gleichfalls ein sehr empfindlicher Indikator ist. Allerdings ist dann die Richtung, in der abgeglichen werden muss, nicht mehr erkennbar, da mit dem Ohr die Phasenlage nicht erkannt werden kann.

Messung mit Schleifdraht-Potentiometer

Schaltplan Wheatstonesche Brückenschaltung (praktisch)

Die durch Gustav Kirchhoff (1824–1887) eingeführte Variante benötigt nur einen Präzisionswiderstand und ein Schleifdraht-Potentiometer. Der Widerstandsdraht ist auf ein Brett gespannt oder auf ein Rohr gewickelt. Die Enden des Drahtes sind mit der Versorgungsspannung verbunden und der Schleifkontakt greift die Teilspannung des Potentiometers ab. Das Längenverhältnis a/b entspricht dabei dem Widerstandsverhältnis $R_{1}/R_{2}$ im Grundaufbau. Im abgeglichenen Zustand berechnet sich der unbekannte Widerstand $R_{x}$ wie folgt:

$R_{x}={\frac ab}\cdot R_{v}$

Die Genauigkeit hängt im Wesentlichen von dem mechanischen Verhältnis a/b und dem Vergleichswiderstand $R_{v}$ ab. In der historischen Anwendung diente ein Galvanometer zur Anzeige der Verstimmung. Um den Nullabgleich präziser durchzuführen, befindet sich ein Taster in Reihe zum Indikator, da eine Bewegung des Zeigers besser erkennbar ist als eine Position.

Wheatstonebrücke mit Schleifdraht-Potentiometer

Der Vergleichswiderstand $R_{v}$ sollte in der Größenordnung wie $R_{x}$ liegen, weil die Genauigkeit zu den Enden des Schleifdrahts nachlässt.

Weiterentwicklung

Die Wheatstonesche Messbrücke wird heute allenfalls noch für Präzisionsmessungen verwendet, siehe auch Kalibrierung. Durch die hohe Genauigkeit der Digitalmultimeter und der Verfügbarkeit von Präzisions-Operationsverstärkern können direkt anzeigende Messverfahren fast überall eingesetzt werden.

Wheatstonesche Messbrücken als Labor-Messgeräte wie das abgebildete sind daher nicht mehr im Handel und professionellen Gebrauch, die Abwandlung zur Ausschlag-Widerstandsmessbrücke dagegen schon.

Die Wheatstone-Brücke ist zur Messung kleiner Widerstände (Richtwert < 1 Ω) nicht geeignet, da die Leitungen und Anschlussklemmen, die den zu messenden Widerstand $R_{x}$ mit dem Messgerät verbinden, die Messung verfälschen. Aus der Wheatstone-Brücke entstand dafür die Thomson-Brücke. Auch diese ist nicht mehr im Handel und professionellen Gebrauch. Zu einer Alternative siehe Widerstandsmessgerät.

Ausschlagverfahren

In der Messtechnik nicht elektrischer Größen ist die Wheatstone-Brücke von erheblicher Bedeutung zur Aufnahme kleiner Widerstandsänderungen aus dem abgeglichenen Zustand heraus. Dann arbeitet sie als Messumformer, z.B. in Zusammenhang

mit temperaturabhängigen Widerständen (Widerstandsthermometer),
mit durch Verformung beeinflussbaren Widerständen (Dehnungsmessstreifen).

Rechnung

In diesen Fällen entsteht eine Spannung $U_{5}$ als Maß für eine Widerstandsänderung $\Delta R$ ; die Brücke arbeitet nach der Ausschlagsmethode. Konkret: Wenn sich aus dem abgeglichenen Zustand heraus $R_{1}$ ändert, $R_{1}$ → $R_1 +\Delta R_1$ , dann entsteht gemäß der eingangs aufgestellten Gleichung

${\frac {U_{5}}{U_{0}}}={\frac {R_{1}+\Delta R_{1}}{R_{1}+\Delta R_{1}+R_{2}}}-{\frac {R_{3}}{R_{3}+R_{4}}}$

Mit der Verstimmung $v={\frac {\Delta R_{1}}{R_{1}}}$ und dem Brückenverhältnis $k={\frac {R_{2}}{R_{1}}}={\frac {R_{4}}{R_{3}}}$ wird

${\frac {U_{5}}{U_{0}}}={\frac {1+v}{1+v+k}}-{\frac {1}{1+k}}=v{\frac {k}{(1+v+k)(1+k)}}$

Solange $|v|\ll 1+k$ oder $|\Delta R_{1}|\ll R_{1}+R_{2}$ gilt die Näherung

${\frac {U_{5}}{U_{0}}}\approx v{\frac {k}{(1+k)^{2}}}\quad ;$ dann ist $U_{5}$ proportional zu $\Delta R_1$ !

Die Funktion $y=f(k)={\frac {k}{(1+k)^{2}}}$ hat ein Maximum bei k=1 und hat dort den Wert $f(1)=\tfrac 14$ . Das heißt, dass die Brücke ein Maximum an Empfindlichkeit hat, wenn sie symmetrisch ist (bei Abgleich alle Widerstände gleich groß = ). Dann ist

$\frac{U_5}{U_0}= \frac14\ \frac{\Delta R_1}R$

Beispiel: Relative Widerstandsänderung $\Delta R_1/R=10^{-3};\ U_0=10\;\mathrm V$ . Dann $U_5=2{,}5\;\mathrm{mV}$ . Das sind noch 25 Digit (Ziffernschritte), falls das Spannungsmessgerät den Messbereich 200 mV in 2000 Digit auflöst.

Das bedeutet: Ohne den Widerstand genau zu kennen, können kleine Änderungen mit derjenigen Qualität bestimmt werden, mit der $U_{5}$ bestimmbar ist. Während die Subtraktion von zwei fast gleich großen Messwerten immer zu sehr unzuverlässigen Ergebnissen führt, wird hier die Differenz in der Schaltung gebildet und ist als solche unmittelbar und zuverlässig messbar!

Erlaubt man allen vier Widerständen jeweils eine kleine Änderung aus dem Abgleich heraus, dann erhält man in der oben zugrundegelegten Anordnung bei einer symmetrischen Brücke

${\frac {U_{5}}{U_{0}}}={\frac 14}\left({\frac {\Delta R_{1}}R}-{\frac {\Delta R_{2}}R}-{\frac {\Delta R_{3}}R}+{\frac {\Delta R_{4}}R}\right)$

Merkregel für die Vorzeichen: Ausgehend vom Einfluss der Änderung eines beliebigen Widerstands auf $U_{5}$ geht die Änderung eines in der Brücke benachbarten Widerstands mit entgegengesetztem Vorzeichen ein und die Änderung des diagonal gegenüberliegenden Widerstands mit gleichem Vorzeichen.

Beispiel: Ändern sich zwei benachbarte Widerstände um je +2 ‰, dann hebt sich ihr Einfluss auf $U_{5}$ auf.

Anwendungen in der Elektronik

Silizium-Drucksensor mit eindiffundierten Widerständen

Auf diese Gleichung wird in der Mikroelektronik und in der Sensortechnik in ganz erheblichem Maße aufgebaut. Auf Dehnung empfindliche Widerstände können auf Verformung je nach Applikation der Widerstände mit positiver oder negativer Widerstandsänderung reagieren und sich in der Gleichung ergänzen, während sich Temperatureinflüsse, die auf alle gleich wirken, aufheben. Widerstände, die sich auf einer elastischen Unterlage befinden, erfassen damit Kräfte, Drücke, Drehmomente usw. Kleine relative Längenänderungen unter 10⁻⁴ können damit noch erfasst werden. Das Bild zeigt ein Druckmessgerät in dieser Technik: Eine Membran aus Silizium, das hochwertige elastische Eigenschaften aufweist, wird durch Druck verformt; an Stellen mit besonders starker Biegung sind Widerstände eindiffundiert; mit jeweils drei Bonddrähten entsteht jeweils die Hälfte einer Wheatstone-Brücke.

Bei der Temperaturmessung mittels Widerstandsthermometer wird nur einer der Widerstände der Brücke veränderbar ausgeführt, in diesem Fall veränderbar durch die Temperatur. Der Messeffekt ist recht komfortabel: Der Widerstand eines genormten Platin-Widerstandsthermometers verdoppelt sich in der Spanne 0 … 266 °C. Deshalb kann mit unsymmetrischer Brücke, $k\gg 1$ , gearbeitet werden, was die Empfindlichkeit vermindert, aber den Bereich vergrößert, in dem die lineare Näherung gilt. Außerdem sorgt bei Anschluss in Dreileiterschaltung die Brückenschaltung für die Eliminierung der Temperatureinflüsse auf die Widerstände der Zuleitungen.

Literatur

Elmar Schrüfer: Elektrische Meßtechnik. Messung elektrischer und nichtelektrischer Grössen. 5. durchgesehene Auflage. Hanser, München u.a. 1992, ISBN 3-446-17128-2.
Siemens Aktiengesellschaft (Hrsg.): Elektromeßtechnik. 5. Auflage. Siemens, Berlin u.a. 1968.
Wilhelm H. Westphal: Physik. 22.–24. Auflage. Springer, Berlin u.a. 1963.

Basierend auf einem Artikel in:

Wikipedia.de