Cooper-Paar

Leon Neil Cooper, Erstbeschreiber

Als Cooper-Paare werden paarweise Zusammenschlüsse von beweglichen Elektronen in speziellen Materialien bezeichnet. Sie treten bei sehr tiefen Temperaturen auf und sind Voraussetzung für den supraleitenden Zustand dieser (metallischen oder keramischen) Materialien. Das Phänomen der Cooper-Paar-Bildung ist nach der Erstbeschreibung im Jahr 1956 durch Leon Neil Cooper benannt und erhält in der BCS-Theorie der Supraleitung grundlegende Bedeutung.

Allgemeiner betrachtet handelt es sich um Paare in fermionischen Vielteilchensystemen, bei denen zwei gepaarte Fermionen ein „zusammengesetztes Boson“ ergeben. Das gleiche Phänomen tritt dadurch auch in anderem Zusammenhang auf, nämlich zwischen jeweils zwei Atomen im supraflüssigen Zustand von ³He unterhalb einer Temperatur von 2,6 mK. Dagegen gibt es im supraflüssigen Zustand von ⁴He keine Cooper-Paare, da hier die Atome Bosonen sind. Eine weitere Möglichkeit zur Bildung von Cooper-Paaren liegt in der Kondensation ultrakalter fermionischer Gase geringer Dichte, mit Methoden der Atomphysik vergleichbar der Bose-Einstein-Kondensation bosonischer Gase.

Auch bei der erst 1986 entdeckten Hochtemperatursupraleitung scheinen Cooper-Paare im Spiel zu sein, wie experimentelle Belege zeigen.^[1] Jedoch ist in diesem Fall, trotz jahrelanger Bemühungen, der zur Paarbildung führende Bindungsmechanismus der beiden Elektronen noch unklar, im Gegensatz zu den seit über 100 Jahren bekannten konventionellen Supraleitern, wie sie weiter unten beschrieben werden und bei denen Phononen die Paarbildung bewirken.

Erklärung

In Metallen können sich die Leitungselektronen praktisch frei zwischen den Atomen bewegen. Dieses „Elektronengas“ besteht aus Fermionen und unterliegt deshalb der Fermi-Verteilung, die eine bestimmte Geschwindigkeitsverteilung von Null bis zu sehr hohen Werten vorhersagt (die charakteristische Temperatur beträgt $T_{F}\sim 10^{4}\,\mathrm {K}$ ). Die Bewegung der Atomkerne spielt dagegen eine vergleichsweise geringe Rolle (die charakteristische Temperatur ist hier die sog. Debye-Temperatur von etwa 150...600 K). Aber erst bei noch tieferen Temperaturen kommt es zu einer nicht mehr zu vernachlässigenden paarweisen Anziehung der Elektronen durch die Atombewegung. Die Stärke dieser Wechselwirkung entspricht Temperaturen von nur etwa 10 K (−263 °C); das entspricht Energien $\Delta E\sim 10^{{-3}}\,{\rm {{eV}}}$ bzw. Lebensdauern der Größe $\Delta \tau \sim \hbar /\Delta E\sim 0{,}7\cdot 10^{-12}\,\mathrm {s}$ . Dabei ist $\hbar$ das reduzierte Plancksche Wirkungsquantum. Das Ergebnis für $\Delta\tau$ entspricht typischen Phonon-Frequenzen, was aber noch nichts beweist: Experimente, die zeigen, dass es sich bei den beteiligten Teilchen tatsächlich um Phononen (quantisierte Atomschwingungen) handelt, und nicht etwa um andersartige Anregungszustände des Systems, beruhen vielmehr auf dem sog. Isotopeneffekt, was Leon Neil Cooper auf die im Folgenden dargestellten Vorstellungen brachte.

Die Bewegung der Atomkerne zieht sich als Wellenphänomen durch das ganze Medium und ergibt (nach Quantisierung) die Phononen. Sie erfolgt aufgrund ihrer höheren Masse zeitlich stark verzögert, woraus eine schwache Polarisation des Gitters resultiert, die die Coulomb-Abstoßung überkompensiert. Ein zweites Elektron kann nun in dieser „Polarisationsspur“ seine Energie absenken, d.h., es wird schwach gebunden. Es entsteht, vermittelt über die Gitterbewegung, ein Cooper-Paar. Die Bildung der Cooper-Paare beruht also – wie alle Polarisationseffekte – auf einer schwachen indirekten Wechselwirkung: Die Elektronen ziehen sich an, weil das System durch die Wechselwirkung polarisiert wird.

Diese Wechselwirkung kann durch folgendes Diagramm beschrieben werden:

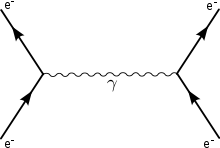
Feynman-Diagramm eines Beitrags zur Elektron-Elektron-Bindung durch „Austausch“ eines Phonons (Zeitachse von unten nach oben; das Phonon, ein Schwingungsquant des Festkörpers, hier mit γ bezeichnet, läuft mit vergleichsweise geringer Geschwindigkeit von links nach rechts oder von rechts nach links).

Man kann den resultierenden Bindungseffekt mit der Bildung einer schwachen Einsenkung in einem Trommelfell unter der Schwerewirkung eines ersten Teilchens vergleichen: Infolgedessen wird ein zweites Teilchen, das sich ebenfalls auf dem Trommelfell bewegt, von dem ersten angezogen, sodass beide aneinander gebunden sind.

Da sich die beiden beteiligten Elektronen in entgegengesetzter Richtung bewegen, ist der Gesamtimpuls des Cooperpaares i.a. klein oder null. Die Impulse müssen also nicht exakt, sondern nur „ungefähr“ entgegengesetzt-gleich sein, damit Paarbildung möglich ist. In der Tat ist die Geschwindigkeit des Suprastromes - und damit dessen Stärke - proportional zur betrachteten Differenz.

Der „Platzbedarf“ jedes Elektrons in einem Cooperpaar wird durch sein Wellenpaket beschrieben. Wenn sich diese voneinander entfernen, zerfallen Cooper-Paare, weil sich die Wellenpakete kaum noch überlappen, andere bilden sich neu.

Schätzt man mit der Unschärferelation die Ausdehnung der Wellenpakete ab, kommt man auf Werte von bis zu 10⁻⁶ m. Ein Vergleich mit den mittleren Abständen der Elektronen im Kristallgitter ergibt das überraschende Ergebnis, dass der Radius des Cooperpaares von der angegebenen Größenordnung sein kann, so dass sich zwischen den Elektronen eines Cooper-Paars mindestens 10¹⁰ andere Elektronen befinden können. Davon haben etwa eine Million anderer Elektronen so ähnliche und überlappende Wellenpakete, dass auch sie Cooper-Paare bilden. Die Cooperpaare sind also fast ebenso zahlreich wie die Elektronen selbst.

Der wesentliche Mechanismus zur Erklärung der Supraleitung (s.u.) ist aber, dass sie im Gegensatz zu den Elektronen, die wegen der Fermi-Statistik einander gewissermaßen „aus dem Wege gehen“, zu einem kohärenten Zustand kondensieren können, wie er für die Supraleitung und generell für sogenannte Supraflüssigkeiten charakteristisch ist. Obwohl die Vertauschungsrelationen zweier Cooperpaare nicht genau denen der Bose-Teilchen entsprechen, sind sie darin diesen doch ähnlich.

Bedeutung bei Supraleitern

Elektronen gehören zur Teilchengruppe der Fermionen, und haben den Spin 1/2 (vgl. Spin-Statistik-Theorem). Die Fermi-Dirac-Statistik ergibt, dass in einem Zweielektronensystem ohne Spin-Bahn-Kopplung deshalb bei symmetrischer Ortsfunktion die Spinfunktion antisymmetrisch sein muss, also etwa $\Psi =\Phi _{{\,{\rm {{symm}}}}}({\vec r}_{1},\,{\vec r}_{2})\cdot (\uparrow \downarrow -\downarrow \uparrow ).$ Anschaulich bedeutet dies, dass der Spin des einen Elektrons nach „oben“ zeigt (d.h., er ist +1/2, in Einheiten der reduzierten Planckschen Konstante $\hbar$ ), während der andere Spin nach „unten“ weist (d.h., er ist −1/2, in denselben Einheiten), also antiparallele Ausrichtung der Spins. Der Gesamtspin des Cooper-Paares ist in diesem Fall null. Dies entspricht dem sogenannten Singulett-Zustand. Ein weiterer, wenn auch seltenerer Fall, ist die parallele Ausrichtung der einzelnen Spins der Cooper-Paar-Elektronen, wobei sich der Gesamtspin zu Eins addiert. Hierbei spricht man vom Triplett-Zustand. Experimentell kann ein solcher Zustand durch Tunnelexperimente nachgewiesen werden, da diese Cooper-Paare durch größere ferromagnetische Barrieren tunneln können.

Für beide Fälle sind die Cooper-Paare aufgrund des ganzzahligen Spins als zusammengesetztes Teilchen keine Fermionen, sondern Bosonen. Für Bosonen gilt aber nicht die Fermi-Dirac-Statistik, sondern die Bose-Einstein-Statistik. Diese besagt – anschaulich gesprochen – dass die Cooper-Paare einem „Herdentrieb“ folgen, so dass sich der oben angesprochene kohärente Zustand ergeben kann: Alle Paare bewegen sich mit der gleichen Geschwindigkeit in die gleiche Richtung und sind streng aneinander gekoppelt.

Der letztgenannte Zusatz bedeutet u.a., dass die Situation im Grunde nicht mit einem Bose-Einstein-Kondensat verglichen werden darf, da die Cooper-Paare nicht als unabhängige Teilchen eines Bose-Gases betrachtet werden können. Dies erklärt dennoch die Eigenschaften metallischer Supraleiter, da die Cooper-Paare als effektive Bose-Teilchen alle ein-und-denselben quantenmechanischen Zustand besetzen dürfen (Anti-Pauli-Prinzip).

Man hat es also auf jeden Fall mit einem makroskopischen, kollektiven Quantenphänomen zu tun.

Da die Ausdehnung der Wellenpakete jedes Cooper-Paars fast schon makroskopisch groß ist, können diese durch dünne Isolatorschichten tunneln (Josephson-Effekt). Experimentell wurde nachgewiesen, dass stets zwei Elektronen die Barriere durchtunneln.

Energielücke

Mathematisch drückt sich die Tendenz zur Bildung von Cooperpaaren dadurch aus, dass im Hamiltonoperator des Systems neben den üblichen bilinearen Termen $\,{\hat a}_{k}^{+}{\hat a}_{k}$ (mit den Elektron-Erzeugungsoperatoren $\,{\hat a}_{k}^{+}$ und den zugehörigen Vernichtungsoperatoren $\,{\hat {a}}_{k}$ ) auch quadratische Terme der ungewöhnlichen Form ${\hat a}_{k}^{+}{\hat a}_{{-k}}^{+}$ und ${\hat {a}}_{k}{\hat {a}}_{-k}$ auftreten:

${\mathcal {H}}=\sum _{k}\,\{\epsilon _{k}\,{\hat a}_{k}^{+}{\hat a}_{k}+\Delta \cdot ({\hat a}_{k}^{+}{\hat a}_{{-k}}^{+}\,+\,{\hat a}_{k}{\hat a}_{{-k}})\}.$ ^[2]

Dabei ist die Wellenzahl der Elektronen, $\epsilon _{k}$ ihre Energie im normalleitenden Zustand und $\Delta$ ein als reell angenommener Paarbildungsparameter.

Grundzustand und angeregte Zustände des Systems werden durch die Wechselwirkung nicht nur quantitativ, sondern auch qualitativ verändert. Die Grundzustandsenergie ist nur leicht erhöht: $E={\sqrt {\epsilon ^{2}+|\Delta |^{2}}}$ , aber – was wesentlicher ist – es bildet sich jetzt eine Energielücke der Größe $\,2|\Delta |$ zu den angeregten Zuständen aus. Das hat u.a. zur Folge, dass der elektrische Widerstand bei entsprechend niedrigen Temperaturen überall Null ist.

Zusammengesetzte Teilchen in der Hochenergiephysik

Die Bildung von zusammengesetzten Teilchen wird auch in der Hochenergiephysik diskutiert, z.B. im Zusammenhang mit dem Higgs-Boson.

Anmerkungen

↑ Cooper-Paar-Bildung in Hochtemperatursupraleitern behandelt ein Artikel der : Max-Plank-Gesellschaft
↑ Die Erzeugungsoperatoren $\,{\hat a}_{k}^{+}$ und Vernichtungsoperatoren $\,{\hat {a}}_{k}$ wirken dabei sowohl auf die -Wellenvektoren als auch auf die Spinzustände.

Basierend auf einem Artikel in:

Wikipedia.de