Weg (Physik)

Ein Weg eines als punktförmig angenommenen Objektes ist der Verlauf seines Ortes bei fortschreitender Zeit infolge seiner Bewegung. Der Weg wird auch als Bahn bezeichnet; er verläuft entlang einer Bahnkurve. Die Position auf dem Weg wird durch einen Ortsvektor relativ zu einem beliebig wählbaren Bezugspunkt beschrieben, welcher als ruhend angenommen wird. Das bevorzugte Formelzeichen zum Weg ist das (von lat. spatium Raum, Ausdehnung, Entfernung).

Teilweise wird mit dem Begriff „Weg“ seine Länge entlang der Bahnkurve gemeint. Zur Unterscheidung wird diese skalare Größe auch als zurückgelegter Weg, Wegstrecke oder Bogenlänge bezeichnet.

Weg als Verlauf des Ortes

→ Hauptartikel: Trajektorie (Physik)

Der Weg als Verlauf des Ortes eines punktförmigen Objekts kann durch Berechnungen als Lösung einer Bewegungsgleichung, die aber nur in sehr einfachen Fällen in geschlossener Form angegeben werden kann, oder durch Messungen z.B. von Teilchen in einer Drahtkammer bestimmt werden. Als Parameter für den Verlauf können entweder die Zeit oder die Wegstrecke gewählt werden: Wahlweise ${\vec {r}}(t)$ oder ${\vec {r}}(s)$ .

Weglänge

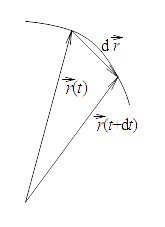
Ortsvektor und Wegelement bei der Bewegung auf einer Bahn

Die Weglänge (vor allem wenn Wellen bzw. Strömungen betrachtet werden auch Lauflänge genannt) von A nach B ist die Summe aller Wegstrecken zwischen A und B. Für genügend kleine, geometrisch einfache oder geradlinige Wegstücke $\Delta s$ gilt:

$s_{\mathrm {AB} }=\sum _{A}^{B}\Delta s\qquad$

Wenn sich ein physikalischer Körper bewegt, so ändert sich sein Ort kontinuierlich im Laufe der Zeit. Die Kurve, die er dabei beschreibt, wird Trajektorie oder Bahnkurve genannt. Das skalare Wegelement $\mathrm d s$ ist der Betrag der infinitesimalen Ortsänderung ${\mathrm d}{\vec r}$ :

$\mathrm {d} s=|\mathrm {d} {\vec {r}}|=|{\vec {v}}(t)|\;\mathrm {d} t$

Bei der Berechnung der Weglänge geht dann die Summation in eine Integration über. Man erhält so die Länge des zwischen den beiden Zeiten zurückgelegten Teils der Bahnkurve:

$s=\int \limits _{(1)}^{(2)}\mathrm {d} s=\int \limits _{t_{1}}^{t_{2}}|{\vec {v}}(t)|\;\mathrm {d} t$

Im Allgemeinen ist die Weglänge länger als die Entfernung zwischen Anfang und Ende der Bahnkurve.

Eine Vereinfachung ergibt sich bei einem eindimensionalen Vorgang: Die Vektoren können durch Skalare ersetzt werden. Beispielsweise bei einem senkrechten Wurf nach oben gilt mit der Fallbeschleunigung , der Anfangsgeschwindigkeit $v_{0}>0$ beim Anfangszeitpunkt $t_{0}=0$ , der Ort-Zeit-Funktion h=0

$v(t)=v_{0}-g\;t$ .

$h(t)=v_{0}\;t-{\frac {g}{2}}\;t^{2}$ .

Der Wurf erreicht eine maximale Steighöhe $h_{\mathrm {max} }={v_{0}}^{2}/(2g)$ ; dort ist v=0 . An dieser Stelle kehrt sein Vorzeichen um. Die Wegstrecke bis zum Ausgangspunkt errechnet sich zu:

$s=\int \limits _{0}^{2v_{0}/g}|v(t)|\;\mathrm {d} t=2\int \limits _{0}^{v_{0}/g}(v_{0}-g\;t)\;\mathrm {d} t={v_{0}}^{2}/g$

Weg in einem physikalischen Feld

Wird ein Objekt in einem physikalischen Feld längs eines Weges vom Ort A zum Ort B verschoben, die durch die Ortsvektoren ${\vec {r}}_{A}$ und ${\vec r}_{B}$ gegeben sind und wirkt auf das Objekt eine Feldkraft ${\vec {F}}$ ein, so wird durch das Feld eine Arbeit $W_{\mathrm {AB} }$ verrichtet

$W_{\mathrm {AB} }=\int _{\mathrm {A} }^{\mathrm {B} }{\vec {F}}\cdot \mathrm {d} {\vec {s}}$ .

Handelt es sich um ein homogenes Feld, so ist ${\vec {F}}$ eine ortsunabhängige Konstante. Dann gilt

$W_{\mathrm {AB} }={\vec {F}}\cdot \left(\int _{\mathrm {A} }^{\mathrm {B} }\mathrm {d} {\vec {s}}\right)={\vec {F}}\cdot {\vec {r}}_{\mathrm {AB} }$

da die Integration des vektoriellen Wegelements $\mathrm {d} {\vec {s}}$ den Verschiebungsvektor ${\vec {r}}_{\mathrm {AB} }$ von A nach B ergibt.

Beispielsweise wird von einem konstanten, homogenen elektrischen Feld mit der Feldstärke ${\vec {E}}$ an einer Ladung , dis sich in diesem Feld von nach bewegt, die Arbeit

$W_{\mathrm {AB} }=q\int _{\mathrm {A} }^{\mathrm {B} }{\vec {E}}\cdot \mathrm {d} {\vec {s}}=q{\vec {E}}\cdot {\vec {r}}_{AB}$

verrichtet.

Wenn ein Feld ein Quellen- oder Potentialfeld ist, dann ist die dadurch verursachte Kraft eine konservativen Kraft. Die Arbeit für die Verschiebung des Körpers von einem Ort zu einem anderen hängt dann nur von der Lage der beiden Orte ab, nicht aber vom Verlauf des Weges dazwischen. Dies meint man, wenn man von einer wegunabhängigen Arbeit spricht.

Entsprechendes gilt für eine bewegte Masse im Gravitationsfeld. Mit der auf eine zeitunabhängige Masse einwirkenden Kraft, die gleich Masse mal Beschleunigung ist, also mit ${\vec {F}}=m{\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}$ ergibt sich

$W_{\mathrm {AB} }=m\int _{\mathrm {A} }^{\mathrm {B} }{\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}\cdot \mathrm {d} {\vec {s}}=m\int _{\mathrm {A} }^{\mathrm {B} }{\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}\cdot {\vec {v}}\,\mathrm {d} t=m\int _{\mathrm {A} }^{\mathrm {B} }{\frac {1}{2}}\,\mathrm {d} (v^{2})={\frac {m}{2}}{v_{\mathrm {B} }}^{2}-{\frac {m}{2}}{v_{\mathrm {A} }}^{2}$ .

Die Arbeit ist nur von der kinetischen Energie bei Anfangs- und Endpunkt abhängig und nicht von der kinetischen Energie während des Weges.

Basierend auf einem Artikel in:

Wikipedia.de