Schönhage-Strassen-Algorithmus

Der Schönhage-Strassen-Algorithmus ist ein Algorithmus zur Multiplikation zweier n-stelliger ganzer Zahlen. Er wurde 1971 von Arnold Schönhage und Volker Strassen entwickelt. Der Algorithmus basiert auf einer sehr schnellen Variante der diskreten schnellen Fourier-Transformation sowie einem geschickten Wechsel zwischen der Restklassen- und der zyklischen Arithmetik in endlichen Zahlenringen.

Der Schönhage-Strassen-Algorithmus terminiert in $O \Big(n \cdot \log(n) \cdot \log \big(\log(n) \big) \Big)$ (siehe Landau-Notation), wenn als Effizienzmaß die Bitkomplexität auf mehrbändigen Turingmaschinen, also die maximale Laufzeit des Algorithmus gemessen als benötigte Bitoperationen in Abhängigkeit von der Bitlänge der Eingabegrößen gewählt wird. Diese Komplexität stellt eine Verbesserung sowohl gegenüber dem naiven aus der Schule bekannten Algorithmus der Laufzeit $O \left(n^2 \right)$ als auch gegenüber dem 1962 entwickelten Karatsuba-Algorithmus mit einer Laufzeit von $O \left(n^{\log_2 (3)} \right)$ sowie dessen verbesserter Variante, dem Toom-Cook-Algorithmus mit $O(n^{1+\varepsilon})$ Laufzeit dar.

Der Schönhage-Strassen-Algorithmus war von 1971 bis 2007 der effizienteste bekannte Algorithmus zur Multiplikation großer Zahlen; 2007 veröffentlichte Martin Fürer eine Weiterentwicklung des Algorithmus mit der noch niedrigeren asymptotischen Komplexität $n\cdot \log(n)\cdot 2^{{O(\log ^{*}(n))}}$ , wobei $\log ^{*}(n)$ der iterierte Logarithmus von n ist. Durch Optimierungen des Algorithmus von Fürer erreichten David Harvey, Joris van der Hoeven und Grégoire Lecerf eine weitere Verbesserung der asymptotischen Laufzeit auf $O(n\cdot \log(n)\cdot 2^{{3\log ^{*}(n)}})$ .

Bedeutung

Bis 2007 konnte kein effizienterer Algorithmus gefunden werden. Als untere Schranke gibt es für den allgemeinen Fall nur die (triviale) lineare Laufzeit, an die sich der Algorithmus mit wachsender Zahlenlänge annähert. Allerdings haben die Forscher Hinweise dafür gefunden, dass die Schranke $O(n \cdot \log(n))$ niemals unterboten werden kann. Selbst bei modernen Computern ist diese Methode der Berechnung erst bei Zahlen mit mehreren tausend Stellen effizienter als der Karatsuba-Algorithmus. Dies liegt wohl allerdings weniger am Overhead des Schönhage-Strassen-Algorithmus, sondern vielmehr an der seit Jahrzehnten typischen Designoptimierung der Computerprozessoren, die dem Erreichen schneller Gleitkommaoperationen den Vorzug vor der Arithmetik in endlichen Restklassenringen ganzer Zahlen gibt.

Für die Suche nach den Algorithmen mit der besten (Zeit-)Komplexität in der Computer-Algebra genießt der Schönhage-Strassen-Algorithmus zentrale Bedeutung.

Algorithmus

Grundidee und Terminologie

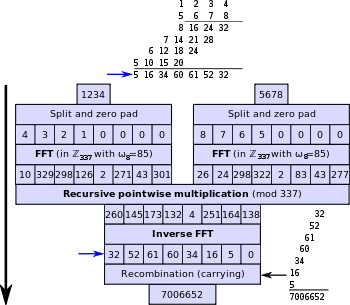
Der Schönhage–Strassen-Algorithmus basiert auf der schnellen diskreten Fourier-Transformation (DFT). Dieses Beispiel zeigt die Berechnung von 1234 × 5678 = 7006652. Die Berechnung findet modulo 337 statt. Um die Anschaulichkeit zu verbessern, wird anstelle der Basis 2 mit Basis 10 gearbeitet.

Um zwei ganze Zahlen und zu multiplizieren, wird im Groben folgendes Schema angewandt:

Aufspaltung der Zahlen (in Binärdarstellung) und in Stücke passender Länge
Schnelle diskrete Fourier-Transformation (DFT) der beiden Stückfolgen
Komponentenweise Multiplikation der transformierten Stücke
Rücktransformation (inverse Fouriertransformation) der Ergebnisse
Zusammensetzen der Ergebnisstücke zur Ergebniszahl

Die im mittleren Schritt durchzuführenden kleinen Multiplikationen werden im rekursiven Sinne wiederum durch den Schönhage-Strassen-Algorithmus ausgeführt.

Um zu verstehen, warum das Ergebnis das Produkt der Zahlen a und b ist, betrachtet man die Polynome

$A = \sum_{i=0}^{2^n-1} a_i \cdot X^i$ und $B = \sum_{i=0}^{2^n-1} b_i \cdot X^i$

Setzt man X = 2 ein, so erhält man gerade die Binärdarstellung der Zahlen a und b. Zu berechnen ist c=C(2) für das Produktpolynom

$C = \sum_{l=0}^{2^{n+1}-1} \sum_{i=0}^l a_i b_{l-i} \cdot X^l$

Wir bestimmen die Fouriertransformierte der Koeffiziententupel von A und B:

$\hat a_k = \sum_{i=0}^{2^n-1} a_i\cdot w^{i\cdot k}$ für $k=0,\ldots,2^n-1$

$\hat b_k = \sum_{j=0}^{2^n-1} b_j\cdot w^{j\cdot k}$ für $k=0,\ldots,2^n-1$

Anders gesagt wertet man die beiden Polynome an den Stellen w^k aus. Multipliziert man nun diese Funktionswerte, so ergeben sich die entsprechenden Funktionswerte des Produktpolynoms

$C=A\cdot B$ .

Um das Polynom selbst zu gewinnen, müssen wir die Transformation rückgängig machen:

$\hat c_l = 1/2^{n+1} \sum_{k=0}^{2^{n+1}-1} \hat a_k \cdot \hat b_k\cdot w^{- l\cdot k}$ für $l=0,\ldots,2^{n+1}-1$

$\hat c_l = 1/2^{n+1} \sum_{i,j,k=0}^{2^{n+1}-1} a_i b_j \cdot w^{i\cdot k + j\cdot k - l\cdot k}$ für $l=0,\ldots,2^{n+1}-1$

$\hat c_l = 1/2^{n+1} \sum_{i,j,k=0}^{2^{n+1}-1} a_i b_j \cdot w^{(i+j-l)\cdot k}$ für $l=0,\ldots,2^{n+1}-1$

Nach Definition der Einheitswurzeln gilt $w^{\,{2^{n+1}}}=1$ . Diese genügt folgender Identität geometrischer Summen von Einheitswurzeln:

$\displaystyle \sum_{k=0}^{{2^{n+1}}-1} w^{lk}=\begin{cases}2^{n+1}&l=0\\0&l\ne 0\end{cases}$ für $l=0,...,2^{n+1}-1$

denn

$\displaystyle \sum_{k=0}^{2^{n+1}-1} x^k=\frac{x^{2^{n+1}}-1}{x-1}$ für $x\neq 1$

Somit gilt:

$\hat c_l = \sum_{i+j=l} a_i b_j$ für $l=0,\ldots,2^{n+1}-1$

Im Artikel Diskrete Fourier-Transformation sind die mathematische Grundlagen dieser Transformation weiter ausgeführt. Da bei der Transformation $2^{n}$ Summen mit jeweils $2^{n}$ Termen entstehen, haben wir bei einer klassischen Berechnung der Terme (etwa durch das Horner-Schema) nach wie vor eine quadratische Laufzeit. Mittels der schnellen Fourier-Transformation kann man diese Werte schneller berechnen. Diese Berechnung beruht auf folgendem Teile-und-herrsche-Prinzip:

$\hat a_k^{even} (w^j) = \sum_{i=0}^{2^n-1} a_j\cdot w^{2j\cdot k}$

$\hat a_k^{odd} (w^j) = \sum_{i=0}^{2^n-1} a_j\cdot w^{(2j+1)\cdot k}$

$\hat a_k (w^j) = a_k^{even} (w^{2j}) + w^k \cdot a_k^{odd} (w^{2j})$

Man setzt Teillösungen mittels einfacher Operationen (Addition und einfache Multiplikation) zusammen. Damit können die Transformationen in Zeit $O(N \cdot \log N)$ berechnet werden. Durch das Runden der komplexen Einheitswurzeln auf feste Stellenlänge ergeben sich jedoch Rechenfehler. Um diese auszugleichen, muss für ein resultierendes Bit mit mindestens $O(\log N)$ Bits gerechnet werden. Daraus ergibt sich eine Gesamtlaufzeit von $O(N\cdot(\log N)^2)$ . Bei der Schönhage-Strassen-Variante rechnen wir stattdessen in einem Restklassenring und vermeiden damit die Rechenfehler der komplexen Zahlen.

Des Weiteren ist die Multiplikation keine reine Faltung, sondern es kann auch zu Überträgen kommen; nach Durchführen der FT und iFT müssen diese passend behandelt werden.

Die Aufgabe der Multiplikation zweier ganzer Zahlen wird nun wie folgt konkretisiert:

Es seien die zwei zu multiplizierenden Zahlen $a,b\in \mathbb {Z}$ in Binärzifferdarstellung gegeben. Weiter sei die maximale Länge (also Binärziffernanzahl) der beiden Zahlen.

Nach passender Behandlung der Vorzeichen der beiden Zahlen sowie der trivialen Sonderfälle a=0 und b=0 (was mit linearem Aufwand O(N) machbar ist) darf man davon ausgehen, dass $a,b\in \mathbb {N}$ natürliche Zahlen sind. Der Schönhage-Strassen-Algorithmus löst diese Aufgabe in $O(N\cdot\log N\cdot \log\log N)$ .

Theoretische Vorbereitungen

Superschnelle DFT

Die oben angesprochene superschnelle DFT, die das Kernstück des Algorithmus darstellt, muss etwas ausführlicher erläutert werden, da sie hier sehr speziell eingesetzt wird.

Es sei ein kommutativer unitärer Ring. In sei das Element eine Einheit; weiterhin sei $w\in R$ eine $2^{n}$ te Einheitswurzel (also $w^{2^n}=1$ ), die die Gleichheit $w^{2^{n-1}} = -1$ erfüllt. Dann lässt sich die Berechnung der diskreten Fouriertransformation (DFT) im Produktraum $R^{2^n}$ (dies ist eine Kurznotation für $R^{(2^n)}$ ; der Begriff Vektorraum ist hier nur für den Fall, dass ein Körper ist, üblich) wie folgt in einer schnellen Variante (als FFT) durchführen:

Zu berechnen ist für $a=(a_0,\ldots,a_{2^n-1})\in R^{2^n}$ die Transformierte $\hat a\in R^{2^n}$ mit

$\hat a_k = \sum_{j=0}^{2^n-1} a_j\cdot w^{j\cdot k}$ für $k=0,\ldots,2^n-1$ .

Indem wir die Indizes $k=\sum_{\nu=0}^{n-1} k_{\nu}\cdot 2^{\nu}$ und $j=\sum_{\nu=0}^{n-1}j_{\nu}\cdot 2^{n-1-\nu}$ in Binärdarstellung aufschreiben, wobei wir dies bei der Zahl in umgekehrter Reihenfolge tun, ist die Transformierte ${\hat {a}}$ wie folgt optimiert berechenbar:

Es seien

$A_0(j_0,\ldots j_{n-1}) = a_j$ für $j=0,\ldots,2^n-1$

und

$A_{r+1}(k_0,\ldots,k_r,j_{r+1},\ldots,j_{n-1}) =$

$= A_r(k_0,\ldots, k_{r-1},0,j_{r+1},\ldots,j_{n-1}) +$

$A_r(k_0,\ldots, k_{r-1},1,j_{r+1},\ldots,j_{n-1})\cdot w^{2^{n-1-r}\cdot (k_r 2^r+\dots +k_0 2^0)}$

$= \sum_{j_r=0}^1 A_r(k_0,\ldots, k_{r-1},j_r,\ldots,j_{n-1}) \cdot w^{j_r 2^{n-1-r}\cdot (k_r 2^r+\dots +k_0 2^0)}$ .

Die geschlossene Darstellung für diese Zwischenterme ist

$A_{r+1}(k_0,\ldots,k_r,j_{r+1},\ldots,j_{n-1}) =$

$= \sum_{j_r=0}^1 \ldots \sum_{j_0=0}^1 a_j \cdot w^{(j_0 2^{n-1}+\ldots + j_r 2^{n-1-r}) \cdot (k_r 2^r+\dots +k_0 2^0)}$ .

(Zum Nachrechnen dieser Darstellung beachte man $w^{(j_0 2^{n-1}+\ldots + j_{r-1} 2^{n-r})\cdot k_r 2^r} = 1$ ).

Diese Rekursion liefert die gewünschten Fourierkoeffizienten $\hat a_k = A_n(k_0,\ldots,k_{n-1})$ .

Aufgrund der Eigenschaft $w^{2^{n-1}}=-1$ können wir den Rekursionsschritt etwas berechnungsfreundlicher umformen zu

$A_{r+1}(k_0,\ldots,k_{r-1},0,j_{r+1},\ldots,j_{n-1}) =$

$= A_r(k_0,\ldots, k_{r-1},0,j_{r+1},\ldots,j_{n-1}) + A_r(k_0,\ldots, k_{r-1},1,j_{r+1},\ldots,j_{n-1})\cdot w^x$

und

$A_{r+1}(k_0,\ldots,k_{r-1},1,j_{r+1},\ldots,j_{n-1}) =$

$= A_r(k_0,\ldots, k_{r-1},0,j_{r+1},\ldots,j_{n-1}) - A_r(k_0,\ldots, k_{r-1},1,j_{r+1},\ldots,j_{n-1})\cdot w^x$

mit dem gleichen Exponenten $x=2^{n-1-r}\cdot (k_{r-1} 2^{r-1}+\ldots + k_0 2^0)$ .

Die Umkehrtransformation, also die inverse FFT, gelingt, da wir vorausgesetzt haben, dass im Ring invertierbar ist:

$A_r(k_0,\ldots,k_{r-1},0,j_{r+1},\ldots,j_{n-1}) =$

$= 2^{-1}\big( A_{r+1}(k_0,\ldots,k_{r-1},0,j_{r+1},\ldots,j_{n-1}) + A_{r+1}(k_0,\ldots,k_{r-1},1,j_{r+1},\ldots,j_{n-1})$

sowie

$A_r(k_0,\ldots,k_{r-1},1,j_{r+1},\ldots,j_{n-1}) =$

$= 2^{-1} w^{-x}\big( A_{r+1}(k_0,\ldots,k_{r-1},0,j_{r+1},\ldots,j_{n-1}) - A_{r+1}(k_0,\ldots,k_{r-1},1,j_{r+1},\ldots,j_{n-1})$ ,

wobei wiederum $x = 2^{n-1-r}\cdot (k_{r-1} 2^{r-1}+\ldots + k_0 2^0)$ ist.

In der Anwendung im Schönhage-Strassen-Algorithmus wird tatsächlich nur eine halbierte FFT benötigt; gemeint ist damit folgendes: Beginnen wir im 1. Schritt der Rekursion mit der Berechnung

$A_1(1,j_1,\ldots,j_{n-1}) = A_0(0,j_1,\ldots, j_{n-1}) - A_0(1,j_1,\ldots, j_{n-1}) = a_j - a_{j+2^{n-1}}$

nur für k_0=1 und schränken wir die weiteren Schritte der Rekursion ebenso auf k_0=1 ein, so berechnen wir gerade alle ${\hat {a}}_{k}$ für ungerade Werte . Will man umgekehrt aus diesen ${\hat {a}}_{k}$ für ungerade (das sind $2^{n-1}$ Stück) lediglich die Differenzen $a_j - a_{j+2^{n-1}}$ der ursprünglichen $a_{j}$ zurückgewinnen, so genügt auch in der Rückrichtung die halbierte Rekursion.

Im Schönhage-Strassen-Algorithmus wird die geschilderte schnelle Fouriertransformation für endliche Zahlenringe $\mathbb {Z} _{F_{n}}$ mit Fermatzahlen $F_n = 2^{(2^n)}+1$ benötigt.

Hinweis zur Notation: Für den Restklassenring ${\mathbb Z}/k{\mathbb Z}$ benutzen wir hier die kürzere Schreibweise $\mathbb {Z} _{k}$ , die lediglich im Kontext der p-adischen Zahlen zu Verwechslungen führen könnte.

Als Einheitswurzel wird im Ring $\mathbb {Z} _{F_{n}}$ die Zahl (oder je nach Kontext auch eine geeignete Potenz von 2) zum Einsatz kommen. Die beim FFT-Algorithmus durchzuführenden Multiplikationen sind dann von der Form $x\cdot 2^k$ ; allerdings sind sie nicht als reine Shift-Operationen durchführbar, da das Reduzieren eines größeren Zwischenergebnisses modulo $F_{n}$ noch nachgeschoben werden muss. Hier greift eine der brillanten Ideen von Schönhage und Strassen: Sie betten den Ring (ausgestattet mit der Restklassenarithmetik) passend in einen größeren, mit der zyklischen Arithmetik ausgestatteten Überring ein. Dieser Überring hat eine 2-Potenz als Ordnung, so dass in ihm die entsprechende Multiplikation tatsächlich als reine Shift-Operation durchführbar ist. Diesen Trick kann man in einem schönen Struktursatz über Restklassen- und zyklische Arithmetik in endlichen Zahlenringen zusammenfassen.

Struktursatz über zyklische Arithmetik

Der Struktursatz über zyklische Arithmetik lässt sich formal wie folgt fassen:

Für eine Zweierpotenz D=2^n mit einer natürlichen Zahl $n\in \mathbb {N}$ gilt

$(\mathbb {Z} _{D+1},+,\cdot )\cong (\mathbb {Z} _{D^{2}},\oplus ,\otimes )/(D+1)\cdot \mathbb {Z}$ .

Hierbei bezeichnet $(\mathbb {Z} _{D+1},+,\cdot )$ die durch die Repräsentanten $0,\ldots,D$ darstellbaren Restklassen modulo D+1 ausgestattet mit der Restklassenarithmetik, d.h. mit der Addition und Multiplikation modulo D+1 . Die in diesem Restklassenring vorkommenden Zahlen können mit n+1 Binärziffern dargestellt werden.

Die auf der rechten Seite vorkommende Struktur $(\mathbb {Z} _{D^{2}},\oplus ,\otimes )$ bezeichnet die Restklassen modulo der Zahl D^2 , die allerdings nicht mit der Restklassenarithmetik, sondern abweichend mit der zyklischen Arithmetik ausgestattet werden. Hierbei werden bei Zwischenergebnissen, die zu groß werden, Überträge aufgehoben und auf das Endergebnis additiv aufgeschlagen. Dies entspricht in Binärzifferdarstellung einer Verschiebung der überständigen Binärziffern (rechtsbündig an die niedrigsten Zifferpositionen gestellt) mit nachfolgender Addition. Beispielsweise ergibt die Addition a+1 mit a=D^2-1 nicht den Wert $D^2\equiv 0$ , sondern den Wert $D^2+1\equiv 1$ . Aus der so erhaltenen Zahlenstruktur mit zyklischer Arithmetik wird nun noch der Faktorring modulo D+1 gebildet. Es werden also die Endergebnisse noch modulo D+1 reduziert.

Damit besagt dieser Struktursatz folgendes: Das modulo-Rechnen in $\mathbb {Z} _{D+1}$ kann ebenso ersetzt werden durch das zyklische Rechnen im größeren Zahlenraum $\mathbb {Z} _{D^{2}}$ mit nachfolgendem Reduzieren modulo D+1 .

Entscheidend für das Gelingen der in diesem Struktursatz vorgestellten Einbettung ist die Eigenschaft, dass die größte darstellbare Zahl im zyklischen Zahlenraum (hier ist dies die Zahl D^2-1 ) die Zahl $0$ aus dem Restklassenring $\mathbb {Z} _{D+1}$ repräsentiert. Hierfür ist die Bedingung (D+1)|F notwendig. Damit die zyklische Arithmetik aber überhaupt sinnvoll definiert werden kann, muss andererseits F+1 eine Zweierpotenz sein. Zusammen ergibt sich, dass F=D^2-1 die optimale Wahl für die Größe des zyklischen Einbettungsraumes darstellt.

Der klassische Restklassenring $(\mathbb {Z} _{D^{2}},+,\cdot )$ wäre für die Einbettung dagegen nicht geeignet, denn in diesem Ring gilt $2^{2n} = D^2 = 0$ , d.h. die Zahl ist in diesem Ring ein Nullteiler.

Durchführung

Haben wir die zu multiplizierenden Zahlen a,b mit $N\leq 2^m$ Binärziffern vorliegen, so führen wir je nachdem, ob gerade oder ungerade ist, unterschiedliche Rekursionsschritte aus, um die Stellenzahl in einem Einzelschritt zu logarithmieren:

Rekursionsschritt für ungerades m

Diesen Schritt der Rückführung von m=2n-1 auf führen wir mit der Komplexität $O\left(2^n \psi(2^n) + n\cdot 2^{2n}\right)$ durch.

Es seien $a,b\in\Z_{F_m}$ mit m=2n-1 und der Fermatzahl $F_m = 2^{2^m}+1$ zu multiplizieren. Wir werden in diesem Schritt die Rückführung auf die Fermatzahl $F_n = 2^{2^n}+1$ vollziehen.

Für die zu den beiden Fermatzahlen gehörenden Zweierpotenzen führen wir die Abkürzungen

$D=F_n-1 = 2^{2^n}$

und

$E = F_m-1 = 2^{2^{2n-1}}=D^{2^{n-1}}$

ein. Die halbierte Stellenzahl von wird unsere Stückelungsgröße werden, d.h. wir entwickeln und nach Potenzen von $\sqrt D$ :

$a = \sum_{i=0}^{2^n} a_i\cdot \sqrt D^i\quad$ und $\quad b = \sum_{i=0}^{2^n} b_i\cdot \sqrt D^i$ ,

wobei für die Einzelstücke $0 \leq a_i, b_i < \sqrt D$ gilt. In Binärdarstellung entspricht diese Zerlegung einer einfachen Gruppierung der Bitfolgen in Stücke der Länge $2^{n-1}$ Bits.

Eine kleine Schwäche des Algorithmus (die allerdings der erreichten Komplexitätsschranke keinen Abbruch tut) offenbart sich jetzt. Um die superschnelle DFT auf die Stückfolgen $(a_0,\ldots,a_{2^n})$ und $(b_0,\ldots,b_{2^n})$ anwenden zu können, müssen diese zur nächsten Zweierpotenzlänge mit Nullen aufgefüllt werden; die Zahlendarstellung wird also künstlich verlängert zu

$a = \sum_{i=0}^{2^{n+1}-1} a_i\cdot \sqrt D^i$ und $b = \sum_{j=0}^{2^{n+1}-1} b_j\cdot \sqrt D^j$ .

Vermöge des oben erwähnten Struktursatzes zur zyklischen Arithmetik wechseln wir nun vom Restklassenring $\mathbb {Z} _{E+1}$ über zum Quotientenraum $(\mathbb {Z} _{E^{2}},\oplus ,\otimes )/(E+1)\cdot \mathbb {Z}$ mit der zyklischen Arithmetik. In diesem Raum errechnet sich für die Multiplikationsaufgabe

$a\cdot b = \left(\sum_{i=0}^{2^{n+1}-1} a_i \sqrt D^i\right)\cdot \left(\sum_{j=0}^{2^{n+1}-1} b_j \sqrt D^j\right)$

$= \sum_{k=0}^{2^{n+2}-2}\left(\sum_{i,j=0\atop i+j=k}^{2^{n+1}-1} a_i\cdot b_j\right) \sqrt D^k$

$= \sum_{k=0}^{2^{n+1}-1}\left(\sum_{i,j=0\atop i+j=k}^{2^{n+1}-1} a_i\cdot b_j\right) \sqrt D^k + \sum_{k=0}^{2^{n+1}-1}\left(\sum_{i,j=0\atop i+j=2^{n+1}+k}^{2^{n+1}-1} a_i\cdot b_j\right) \sqrt D^{2^{n+1}+k}$

$= \sum_{k=0}^{2^{n+1}-1}\left(\sum_{i,j=0\atop i+j\equiv k \mod 2^{n+1}}^{2^{n+1}-1} a_i\cdot b_j\right) \sqrt D^k$ ,

wobei wir im letzten Schritt die Eigenschaft $\sqrt D^{2^{n+1}} = D^{2^n} = E^2 = 1$ in diesem zyklischen Zahlenraum benutzt haben.

Zusammenfassend erhält die Multiplikation also die Form

$a\cdot b = \sum_{k=0}^{2^{n+1}-1} c_k \sqrt D^k$

mit den Ergebniskoeffizienten

$c_k = \sum_{i,j=0\atop i+j\equiv k\mod 2^{n+1}}^{2^{n+1}-1} a_i\cdot b_j$ .

Wir können $c_k < 2^{n+1}D$ nach oben abschätzen.

Nun folgt eine Umschreibung der Summenformel, damit wir uns bei der anzuwendenden FFT auf eine halbierte FFT beschränken können.

Es gilt $c_{k+2^n} \sqrt D^{k+2^n} = c_{k+2^n} \sqrt D^k E = - c_{k+2^n}\sqrt D^k$ , also ist

$a\cdot b = \sum_{k=0}^{2^n-1} (c_k - c_{k+2^n}) \sqrt D^k$

mit $-2^{n+1}D < c_k - c_{k+2^n} < 2^{n+1}D$ in $\mathbb {Z} _{E+1}$ . Durch passende Addition können wir den Wertebereich ins Positive verschieben, es ist nämlich $0 < c_k - c_{k+2^n} + 2^{n+1}D < 2^{n+2}D$ , und mit der Definition

$z_k = \Big\lbrace {c_k - c_{k+2^n} + 2^{n+1}D, \quad 0\leq k < 2^n \atop 2^{n+1}D, \quad\quad 2^n\leq k < 2^{n+1} }$

gilt

$a\cdot b = \sum_{k=0}^{2^{n+1}-1} z_k \sqrt D^k$ .

Für die nichttrivialen z_k (Indizes $0$ bis 2^n-1 ) gilt die Abschätzung $0 < z_k < 2^{n+2}D < 2^{n+2}F_n$ . Da die beiden Zahlen $2^{n+2}$ und $F_{n}$ teilerfremd ist, genügt zur Bestimmung der z_k die Berechnung der Reste $z_k \mod 2^{n+2}$ und $z_k \mod F_n$ .

Hat man nämlich die Reste $z_k=\xi \mod F_n$ und $z_k=\eta \mod 2^{n+2}$ bestimmt, so kann man in Komplexität O(2^n) wie folgt rechnen: Berechne erst $\delta = \eta - \xi \mod 2^{n+2}$ und dann $z_k = \xi + \delta\cdot (D+1) = \xi + \delta\cdot F_n$ .

Bestimmung der Reste modulo 2ⁿ⁺²

Hier wenden wir einen für die Computeralgebra sehr typischen Trick an: Wir setzen die Stückfolgen $a_{i}$ und $b_{i}$ durch Einfügen genügend langer Nullsequenzen mit Sicherheitsabständen so zusammen, dass nach Produktbildung die Einzelergebnisse ebenfalls noch ohne Überlappungen in Stücken aneinandergereiht sind. Es seien also $\alpha_j = a_j\mod 2^{n+2}$ und $\beta_j = b_j\mod 2^{n+2}$ in $\mathbb {Z} _{2^{n+2}}$ . Wir bilden nun

$u = \sum_{k=0}^{2^{n+1}-1}\alpha_k 2^{k(3n+5)}$ und $v = \sum_{k=0}^{2^{n+1}-1}\beta_k 2^{k(3n+5)}$

und haben dabei $0 \leq u, v < 2^{2^{n+1}(3n+5)}$ . Das Produkt $u\cdot v$ enthält dann in disjunkten Stücken der Bitlänge 3n+5 die Summen

$\gamma_k = \sum_{r,s=0 \atop r+s=k}^{2^{n+1}-1}\alpha_r\cdot \beta_s$

mit $0\leq k < 2^{n+2}$ , denn es ist $0\leq \gamma_k < 2^{3n+5}$ . Für die Terme c_k unserer ursprünglichen Multiplikationsaufgabe $a\cdot b$ sehen wir

$c_k = \gamma_k + \gamma_{k+2^{n+1}}\mod 2^{n+2}$ .

Für die zu bestimmenden Reste $\eta_k = z_k \mod 2^{n+2}$ erhalten wir

$\eta_k = \gamma_k - \gamma_{k+2^n } + \gamma_{k+2\cdot 2^n} - \gamma_{k+3\cdot 2^n}$ in $\mathbb {Z} _{2^{n+2}}$ .

Der Komplexitätsaufwand für die Bildung aller $\alpha_j, \beta_j$ sowie der Extraktion der $\eta_k$ ist $O(2^{2n})$ ; die Multiplikation $u\cdot v$ kostet $\psi(2^{n+1}(3n+5))$ , insgesamt ist dies also $O(2^{2n})$ .

Bestimmung der Reste modulo (D+1)

Hier kommt die DFT zum Einsatz. Wir unterziehen die Vektoren $(a_0,\ldots a_{2^{n+1}-1})$ und $(b_0,\ldots b_{2^{n+1}-1})$ mit $0 \leq a_k, b_k < \sqrt D$ der DFT in $R^{2^{n+1}}$ mit $R=\mathbb {Z} _{D+1}$ und der Zahl als $2^{n+1}$ -ter Einheitswurzel. Da wir nur die Differenzen $c_k - c_{k+2^n}$ benötigen, genügt die halbierte DFT:

DFT zur Bestimmung der ${\hat {a}}_{k}$ und $\hat b_k$ nur für die ungeraden mit $0\leq k < 2^{n+1}$
$2^{n}$ Multiplikationen $\hat c_k = \hat a_k\cdot \hat b_k$ für alle ungeraden
Inverse DFT zur Gewinnung aller Differenzen $c_k - c_{k+2^n}$ aus den $\hat c_k$ für ungerade

Der Komplexitätsaufwand hierfür besteht aus O(n 2^n) Schritten des Einzelaufwands O(2^n) für die DFT (gesamt also $O(n 2^{2n})$ ); hinzu kommen die Addition von $2^{n+1}D$ sowie die Reduktionen modulo (D+1) für die Gewinnung der $z_k \mod (D+1)$ , was in $O(2^{2n})$ bewältigt werden kann.

Rekursionsschritt für gerades m

Auch für diesen Schritt der Rückführung von m=2n-2 auf wird die Komplexität $O\left(2^n \psi(2^n) + n\cdot 2^{2n}\right)$ erreicht.

Es seien $a,b\in\Z_{F_m}$ mit m=2n-2 und der Fermatzahl $F_m = 2^{2^m}+1$ zu multiplizieren. Wir werden auch in diesem Schritt die Rückführung auf die Fermatzahl $F_n = 2^{2^n}+1$ vollziehen.

Für die zu den beiden Fermatzahlen gehörenden Zweierpotenzen führen wir analog die Abkürzungen

$D=F_n-1 = 2^{2^n}$

und

$E = F_m-1 = 2^{2^{2n-2}}=D^{2^{n-2}}$

ein. Wiederum wird die halbierte Stellenzahl von unsere Stückelungsgröße werden, d.h. wir entwickeln und nach Potenzen von $\sqrt D$ :

$a = \sum_{i=0}^{2^{n-1}} a_i\cdot \sqrt D^i\quad$ und $\quad b = \sum_{i=0}^{2^{n-1}} b_i\cdot \sqrt D^i$ ,

wobei für die Einzelstücke $0 \leq a_i, b_i < \sqrt D$ gilt.

Wie oben verlängern wir die Zahlendarstellung auf Zweierpotenzlänge zu

$a = \sum_{i=0}^{2^n-1} a_i\cdot \sqrt D^i$

und analog für .

Unter abermaliger Zuhilfenahme des Struktursatzes zur zyklischen Arithmetik wechseln wir nun vom Restklassenring $\mathbb {Z} _{E+1}$ über zum Quotientenraum $(\mathbb {Z} _{E^{2}},\oplus ,\otimes )/(E+1)\cdot \mathbb {Z}$ mit der zyklischen Arithmetik.

Damit können wir wieder

$a\cdot b = \sum_{k=0}^{2^n-1} c_k \sqrt D^k$

mit den Ergebniskoeffizienten

$c_k = \sum_{r,s=0\atop r+s\equiv k\mod 2^n}^{2^n-1} a_r\cdot b_s$

darstellen. Dabei können wir c_k < 2^n D nach oben abschätzen.

Aus $\sqrt D^{2^{n-1}} = E^2=1$ können wir wieder

$0 < c_k - c_{k+2^{n-1}} + 2^n D < 2^{n+1} D$

folgern, und mit

$z_k = \Big\lbrace {c_k - c_{k+2^{n-1}} + 2^n D, \quad 0\leq k < 2^{n-1} \atop 2^n D, \quad\quad 2^{n-1}\leq k < 2^n}$

gilt

$a\cdot b = \sum_{k=0}^{2^n-1} z_k \sqrt D^k$

mit $0<z_k < 2^{n+1} D$ . Für die nichttrivialen z_k (Indizes $0$ bis $2^{n-1}-1$ ) gilt die Abschätzung $0 < z_k < 2^{n+1}D < 2^{n+1}F_n$ . Wegen der Teilerfremdheit der beiden Zahlen $2^{n+1}$ und $F_{n}$ genügt es wieder zur Bestimmung der z_k , die Reste $z_k \mod 2^{n+2}$ und $z_k \mod F_n$ zu berechnen.

Bestimmung der Reste modulo 2ⁿ⁺¹

Wir wenden wieder den Trick der Einfügung von Sicherheitsabständen an: Es seien also $\alpha_j = a_j\mod 2^{n+1}$ und $\beta_j = b_j\mod 2^{n+1}$ in $\mathbb {Z} _{2^{n+1}}$ . Wir bilden

$u = \sum_{k=0}^{2^n-1}\alpha_k 2^{k(3n+2)}$ und $v = \sum_{k=0}^{2^n-1}\beta_k 2^{k(3n+2)}$

und haben dabei $0 \leq u, v < 2^{2^n(3n+2)}$ . Das Produkt $u\cdot v$ enthält dann in disjunkten Stücken der Bitlänge 3n+2 die Summen

$\gamma_k = \sum_{r,s=0 \atop r+s=k}^{2^n-1}\alpha_r\cdot \beta_s$

mit $0\leq k < 2^{n+1}$ . Für die gesuchten c_k unserer ursprünglichen Multiplikationsaufgabe $a\cdot b$ sehen wir

$c_k = \gamma_k + \gamma_{k+2^n}\mod 2^{n+1}$ .

Für die zu bestimmenden Reste $\eta_k = z_k \mod 2^{n+1}$ erhalten wir

$\eta_k = \gamma_k - \gamma_{k+2^{n-1}} + \gamma_{k+2\cdot 2^{n-1}} - \gamma_{k+3\cdot 2^{n-1}}$ in $\mathbb {Z} _{2^{n+1}}$ .

Bestimmung der Reste modulo (D+1)

Mit $R=\mathbb {Z} _{D+1}$ unterziehen wir wieder die Vektoren $(a_{0},\ldots a_{{2^{n}-1}})$ und $(b_0,\ldots b_{2^n-1})$ mit $0 \leq a_k, b_k < \sqrt D$ der DFT in $R^{2^n}$ , wobei wir diesmal die Zahl als $2^{n}$ -te Einheitswurzel wählen. Da wir nur die Differenzen $c_k - c_{k+2^{n-1}}$ benötigen, genügt hier wiederum die halbierte DFT:

DFT zur Bestimmung der ${\hat {a}}_{k}$ und $\hat b_k$ nur für die ungeraden mit $0\leq k<2^{n}$
$2^{n-1}$ Multiplikationen $\hat c_k = \hat a_k\cdot \hat b_k$ für alle ungeraden
Inverse DFT zur Gewinnung aller Differenzen $c_k - c_{k+2^{n-1}}$ aus den $\hat c_k$ für ungerade

Zusammenfassung

Startend mit und mit Ziffernlänge wird durch die dargestellte Rekursion eine Komplexität von $O (n \cdot \log(n) \cdot \log (\log(n) ) )$ erreicht.

Abgewandelte Form

Zimmermann und Brent beschreiben eine Variante des Algorithmus, bei der die Laufzeit (in Abhängigkeit von der Länge der Eingabe) keine Sprünge macht, sondern stetiger verläuft. Dies wird erreicht, indem die DFT-Vektoren nicht aus $2^{n}$ -stelligen Binärzahlen, sondern Zahlen der passenden Länge gebildet werden. Dadurch muss die Länge der zu transformierenden Vektoren keine Zweierpotenz sein.

Basierend auf einem Artikel in:

Wikipedia.de

Schönhage-Strassen-Algorithmus

Bedeutung

Algorithmus

Grundidee und Terminologie

Theoretische Vorbereitungen

Superschnelle DFT

Struktursatz über zyklische Arithmetik

Durchführung

Rekursionsschritt für ungerades m

Bestimmung der Reste modulo 2n+2

Bestimmung der Reste modulo (D+1)

Rekursionsschritt für gerades m

Bestimmung der Reste modulo 2n+1

Bestimmung der Reste modulo (D+1)

Zusammenfassung

Abgewandelte Form

Bestimmung der Reste modulo 2ⁿ⁺²

Bestimmung der Reste modulo 2ⁿ⁺¹