Satz von Gauß über das vollständige Vierseit

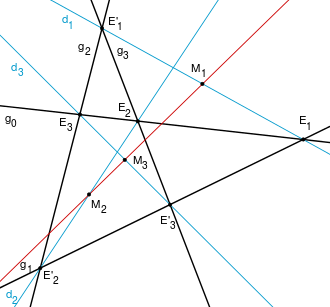
4 Seiten (schwarz), 3 Diagonalen (blau), gemeinsame Gerade der Diagonalemitten (rot)

Der Satz von Gauß über das vollständige Vierseit ist ein Satz der affinen Geometrie. Er geht zurück auf Carl Friedrich Gauß (1777–1855), welcher ihn im Jahre 1810 fand. Der Satz gehört in die Reihe der sogenannten Schließungssätze, zu denen unter anderem auch der Satz von Pappos-Pascal, der Satz von Desargues, der Satz von Menelaos und der Satz von Ceva gehören.

Klärung der Begriffe

Gegeben sei ein affiner Raum $\mathcal{A}$ über einem Körper mit $2=1+1\neq 0$ . Ein vollständiges Vierseit ${\mathcal {Q}}$ in $\mathcal{A}$ (engl. manchmal als quadrilateral oder eher als complete quadrilateral bezeichnet) besteht aus vier verschiedenen Geraden $g_{0},\,g_{1},\,g_{2},\,g_{3}$ , die sich paarweise schneiden, von denen jedoch keine drei durch ein und denselben Punkt von $\mathcal{A}$ gehen.

Die Ecken des vollständigen Vierseits

Die paarweisen Schnittpunkte der vier Ausgangsgeraden werden als Ecken des vollständigen Vierseits ${\mathcal {Q}}$ bezeichnet und bilden die Eckenmenge ${\mathcal {E}}={\mathcal {E}}({\mathcal {Q}})$ . Dabei gehört zu jeder 2-Menge von Geraden ${\{g_{k},\,g_{l}\}}_{\neq }\subset {\{g_{0},\,g_{1},\,g_{2},\,g_{3}\}}$ umkehrbar eindeutig die Ecke $E=g_{k}\cap g_{l}$ von ${\mathcal {Q}}$ , was insgesamt zu

$|{\mathcal {E}}|={\binom {4}{2}}=6$

${\mathcal {Q}}$ -Ecken führt.

Weiter liegen auf jeder Geraden $g_{k}(k=0,\,1,\,2,\,3)$ genau drei Ecken, nämlich denjenigen Ecken, welche als Schnittpunkte $g_{k}\cap g_{j}$ von $g_{k}$ mit den übrigen Geraden $g_{j}(j\neq k)$ entstehen.

Darüber hinaus gehört zu jeder Ecke $E=g_{k}\cap g_{l}({\{g_{k},\,g_{l}\}}_{\neq }\subset {\{g_{0},\,g_{1},\,g_{2},\,g_{3}\}})$ umkehrbar eindeutig die Gegenecke oder Komplementärecke $E^{'}$ , welche man dadurch gewinnt, dass man das zugehörige Komplement ${\{g_{0},\,g_{1},\,g_{2},\,g_{3}\}}\setminus {\{g_{k},\,g_{l}\}}={\{g_{m},\,g_{n}\}}$ bildet und dann die zu gehörige Gegenecke als $E^{'}=g_{m}\cap g_{n}$ .

Das Bilden der Gegenecke ist eine involutorische Abbildung auf ${\mathcal {E}}$ :

$E^{''}=E$ $(E\in {\mathcal {E}})$ .

Die Eckenmenge ${\mathcal {E}}$ lässt sich demnach schreiben wie folgt:

${\mathcal {E}}=\{E_{1},\,{E_{1}}^{'},\,E_{2},\,{E_{2}}^{'},\,E_{3},\,{E_{3}}^{'}\}$ mit

$E_{1}=g_{0}\cap g_{1}$ ${E_{1}}^{'}=g_{2}\cap g_{3}$

$E_{2}=g_{0}\cap g_{2}$ ${E_{2}}^{'}=g_{1}\cap g_{3}$

$E_{3}=g_{0}\cap g_{3}$ ${E_{3}}^{'}=g_{1}\cap g_{2}$

Führt man diese Überlegung mit einer der drei von $g_{0}$ verschiedenen Geraden statt mit $g_{0}$ durch, so erhält man eine entsprechend andere, aber gleichwertige Darstellung der Eckenmenge ${\mathcal {E}}={\mathcal {E}}({\mathcal {Q}})$ . Der Zusammenhang zwischen Ecken und Gegenecken ist von der Art der Darstellung der Eckenmenge unberührt und allein von der der vier Ausgangsgeraden abhängig.

Die Ebene des vollständigen Vierseits

Der Verbindungsraum ${\mathcal {P}}=g_{0}\lor g_{1}$ ist eine affine Ebene innerhalb ${\mathcal {A}}$ , welche die gesamte Eckenmenge ${\mathcal {E}}$ enthält:

Dies ist für die Ecken $E_{1},\,E_{2},\,E_{3},\,{E_{2}}^{'},\,{E_{3}}^{'}$ unmittelbar klar. Wegen $g_{2}=E_{2}\lor {E_{3}}^{'}$ enthält ${\mathcal {P}}$ dann aber auch die Gerade $g_{2}$ und damit schließlich ${E_{1}}^{'}$ .

${\mathcal {P}}$ ist also unabhängig von der Art der Darstellung der Eckenmenge ${\mathcal {E}}$ die zum vollständigen Vierseit ${\mathcal {Q}}$ gehörige und von diesem erzeugte Ebene ${\mathcal {P}}={\mathcal {P}}({\mathcal {Q}})$ innerhalb ${\mathcal {A}}$ .

Die Diagonalen des vollständigen Vierseits und deren Mittelpunkte

Nach Konstruktion liegen für keinen Index $i=1,\,2,\,3$ die beiden ${\mathcal {Q}}$ -Ecken $E_{i}$ und ${E_{i}}^{'}$ zugleich auf einer der vier gegebenen Geraden $g_{0},\,g_{1},\,g_{2},\,g_{3}$ . Verbindet man also jede Ecke $E_{i}$ von ${\mathcal {Q}}$ mit der Gegenecke ${E_{i}}^{'}$ , so erhält man zu den vier gegebenen Geraden drei weitere Geraden $d_{1},\,d_{2},\,d_{3}$ hinzu. Dies sind die Diagonalen des vollständigen Vierseits ${\mathcal {Q}}$ :

$d_{1}=E_{1}\lor {E_{1}}^{'}$

$d_{2}=E_{2}\lor {E_{2}}^{'}$

$d_{3}=E_{3}\lor {E_{3}}^{'}$

Zu jeder der drei Diagonalen $d_{i}(i=1,\,2,\,3)$ existiert unter den Punkten, die mit $d_{i}$ inzidieren, jeweils ein ausgezeichneter Punkt $M_{i}$ . Diesen Punkt nennt man den Mittelpunkt der Diagonalen $d_{i}$ oder kurz die Mitte der Diagonalen $d_{i}$ . Der Mittelpunkt der Diagonalen $d_{i}$ erfüllt die Gleichungen:

${\overrightarrow {{E_{i}}{M_{i}}}}={\tfrac {1}{2}}\cdot {\overrightarrow {{E_{i}}{E_{i}}^{'}}}={\overrightarrow {{M_{i}}{{E_{i}}^{'}}}}$

und

$E_{i}+{\tfrac {1}{2}}\cdot {\overrightarrow {{E_{i}}{E_{i}}^{'}}}=M_{i}={E_{i}}^{'}-{\tfrac {1}{2}}\cdot {\overrightarrow {{E_{i}}{E_{i}}^{'}}}$

und ist dadurch eindeutig bestimmt.

Von diesen drei Mittelpunkten der Diagonalen des vollständigen Vierseits ${\mathcal {Q}}$ handelt der Satz von Gauß.

Formulierung

Der Satz lautet wie folgt:

In einem affinen Raum über einem Körper der Charakteristik $\operatorname {char} (K)\neq 2$ liegen die Mittelpunkte der Diagonalen eines vollständigen Vierseits stets auf einer Geraden, der sogenannten Gauß-Geraden.

Der Fall der euklidischen Ebene

Der Satz gilt insbesondere für den Fall, dass ${\mathcal {A}}={\mathbb {A} }_{2}(K)$ , also die Koordinatenebene über ist. Ein besonders hervorzuhebender Fall liegt hierbei dann vor, wenn $K=\mathbb {R}$ ist, also der Körper der reellen Zahlen vorliegt und wenn dann der gegebene affine Raum ${\mathcal {A}}$ mit der euklidischen Ebene zusammenfällt.

Unter diesen Gegebenheiten lässt sich der Satz dann so aussprechen:

Wenn vier Geraden so in der euklidischen Ebene liegen, dass keine drei davon durch einen Punkt gehen, so liegen die Mitten der zugehörigen Diagonalen stets auf einer Geraden.

Literatur

Gerrit Bol: Elemente der Analytischen Geometrie. 1. Teil. Vandenhoeck & Ruprecht, Göttingen 1948.
Max Koecher, Aloys Krieg: Ebene Geometrie (= Springer-Lehrbuch). 2., neu bearbeitete und erweiterte Auflage. Springer Verlag, Berlin (u.a.) 2000, ISBN 3-540-67643-0.

Basierend auf einem Artikel in:

Wikipedia.de