Holonomie
Der mathematische Begriff der
Holonomiegruppe eines Zusammenhangs
eines Vektor-
oder Hauptfaserbündels
über einer differenzierbaren
Mannigfaltigkeit (abgekürzt auch einfach Holonomie) bezeichnet in der
Differentialgeometrie
die Gruppe linearer
Transformationen, die durch den Paralleltransport
von Vektoren entlang geschlossener Kurven induziert wird. Trägt eine
Mannigfaltigkeit
eine riemannsche
Metrik, so ist deren riemannsche
Holonomie durch die Holonomie des Levi-Civita-Zusammenhangs
auf dem Tangentialbündel
von
gegeben.
Beispiele
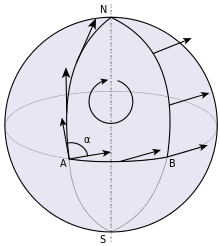
Als Beispiel betrachten wir die Kugeloberfläche
mit der Standardmetrik aus dem
. Wir fixieren einen Punkt auf der Kugeloberfläche, etwa
wie in nebenstehender Zeichnung. Ein Element des Tangentialraums
ist dann ein tangential an der Kugeloberfläche anliegender Vektor mit Ursprung
in
.
Wie in nebenstehender Zeichnung angedeutet, betrachten wir den Paralleltransport
dieses Vektors längs des geschlossenen Weges
.
Dabei wird deutlich, dass der verschobene Vektor im Punkt
im Vergleich zum Ausgangsvektor um einen gewissen Winkel gedreht wurde, und es
ist klar, dass jeder andere Vektor aus
durch diesen Paralleltransport um denselben Winkel gedreht wird, d.h., die
Drehung um diesen Winkel auf dem Raum
ist ein Element der Holonomiegruppe im Punkt
.
Genauso klar ist, dass man durch Verwendung anderer geschlossener Wege auf der
Kugeloberfläche jeden Drehwinkel erhalten kann. Damit ist die Holonomiegruppe im
Punkt
isomorph zur Gruppe
der Drehungen im zweidimensionalen Raum. Da die Kugeloberfläche wegzusammenhängend ist,
erhält man in jedem Punkt eine isomorphe Holonomiegruppe. Ist nämlich
ein anderer Punkt und
ein Weg von
nach
,
so erhält man aus einem Paralleltransport am Punkt
einen solchen am Punkt
,
indem man einen Tangentialvektor an
zunächst längs
parallel nach
verschiebt, dort den gegebenen Paralleltransport am Punkt
anwendet und das Ergebnis längs des umgekehrten Weges
wieder zurück nach
verschiebt. Das definiert offenbar einen Isomorphismus zwischen den
Holonomiegruppen an
und
.
Betrachtet man als weiteres Beispiel den euklidischen
Raum
mit der euklidischen Metrik, also dem Standardskalarprodukt, so fällt der
Parallelitätsbegriff mit der geometrischen Parallelität zusammen. Eine wie auch
immer geartete Parallelverschiebung eines Vektors ändert dessen Richtung nicht.
Wenn man also längs eines geschlossenen Weges parallelverschiebt, so erhält man
den Ausgangsvektor zurück, das heißt, ein Paralleltransport an einem gegebenen
Punkt ist immer die identische
Abbildung. Daher ist die Holonomiegruppe in diesem Fall trivial.
Bedeutung in der Physik
Holonomiegruppen spielen eine große Rolle in der theoretischen Physik, sowohl in der Quantenfeldtheorie, als auch im Besonderen in der Stringtheorie. Hier ist die Holonomiegruppe von kompakten sechs- und siebendimensionalen Mannigfaltigkeiten von Interesse, da bei einer Kompaktifizierung der Theorie auf diesen Räumen die Anzahl der erhaltenen Supersymmetrie von der maximalen Anzahl kovariant konstanter Spinoren abhängt, die wiederum von der Holonomie bestimmt wird. Mannigfaltigkeiten von besonderem Interesse sind sechsdimensionale Calabi-Yau-Mannigfaltigkeiten mit SU(3)-Holonomie sowie siebendimensionale Mannigfaltigkeiten mit G2-Holonomie.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 18.08. 2021