Dichte

Name

Massendichte

$\rho$

Größen- und Einheitensystem	Einheit	Dimension
SI	kg·m⁻³	M·L⁻³

Siehe auch: Wichte (spezifisches Gewicht),
relative Dichte (spezifische Dichte),
spezifisches Volumen

Die Dichte $\rho$ (Rho), auch Massendichte genannt, ist der Quotient aus der Masse eines Körpers und seinem Volumen :

$\rho ={\frac {m}{V}}$ .

Sie wird oft in Gramm pro Kubikzentimeter oder in Kilogramm pro Kubikmeter angegeben. Bei flüssigen Körpern ist auch die Einheit Kilogramm pro Liter üblich. Die Dichte ist durch das Material des Körpers bestimmt und als intensive Größe unabhängig von seiner Form und Größe.

Im Allgemeinen dehnen sich Stoffe mit steigender Temperatur aus, wodurch ihre Dichte sinkt. Eine Ausnahme bilden Stoffe mit einer Dichteanomalie wie z.B. Wasser.

Abgrenzung zu anderen Begriffen

Während bei der Dichte die Masse im Verhältnis zum Volumen steht, gibt die Wichte die Gewichtskraft im Verhältnis zum Volumen an, ist also abhängig vom Schwerefeld.
Die relative Dichte ist das Verhältnis der Dichte zur Dichte eines Normals, also eine dimensionslose Größe.

Definiert werden diese Unterschiede in der DIN 1306 Dichte; Begriffe, Angaben. Die Dichte ist eine Quotientengröße.

Bestimmung der Dichte

Dichtebestimmung durch Auftrieb

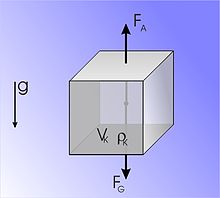
An einem eingetauchten Körper angreifende Kräfte

Nach dem Prinzip von Archimedes erfährt ein vollständig in einem Fluid (einer Flüssigkeit oder einem Gas) eingetauchter Körper eine Auftriebskraft, die gleich der Gewichtskraft des Volumens des verdrängten Stoffes ist. Um die zwei Unbekannten Dichte und Volumen zu bestimmen, sind zwei Messungen erforderlich.

Taucht man einen beliebigen Körper mit dem Volumen $V_{{\mathrm K}}$ vollständig in zwei Fluide mit bekannten Dichten $\rho _{1}$ und $\rho _{2}$ ein, ergeben sich resultierende Kräfte $F_{1}$ und $F_{2}$ , die mittels einer einfachen Waage messbar sind. Die gesuchte Dichte $\rho _{{\mathrm K}}$ des Körpers lässt sich daraus wie folgt bestimmen:

Ausgehend von den Formeln für die Gewichtskraft $F_{{\mathrm G}}$ des Körpers und die Auftriebskraft $F_{{{\mathrm A}i}}$ des Körpers in Fluid

$F_{{\mathrm G}}=V_{{\mathrm K}}\cdot \rho _{{\mathrm K}}\cdot g$

$F_{{{\mathrm A}i}}=V_{{\mathrm K}}\cdot \rho _{i}\cdot g$

mit der Schwerebeschleunigung misst eine Waage für den in Fluid eingetauchten Körper die Kraft

$F_{i}=F_{{\mathrm G}}-F_{{{\mathrm A}i}}.$

Aus diesen zwei Gleichungen für die Fluide ( i=1,2 ) kann man das unbekannte Volumen $V_{{\mathrm K}}$ eliminieren und erhält die Lösung:

$\rho _{{\mathrm K}}={\frac {F_{1}\cdot \rho _{2}-F_{2}\cdot \rho _{1}}{F_{1}-F_{2}}}$

Falls eine Dichte sehr viel kleiner als die andere ist, $\rho_1 \ll \rho_2$ (etwa bei Luft und Wasser), vereinfacht sich die Formel zu:

$\rho _{{\mathrm K}}={\frac {F_{1}}{F_{1}-F_{2}}}\cdot \rho _{2}$

Falls man nur eine Flüssigkeit, z.B Wasser mit Dichte $\rho _{1}$ hat, lässt sich stattdessen das Volumen des Körpers durch das Volumen des Wassers bestimmen, das bei vollständigem Eintauchen verdrängt wird, indem man beispielsweise den Überlauf aus einem vollen Gefäß mit einem Messzylinder misst. Aus obiger Gleichung

$F_{1}=F_{{\mathrm G}}-F_{{{\mathrm A}1}}=V_{{\mathrm K}}\cdot g\cdot (\rho _{{\mathrm K}}-\rho _{1})$

erhält man durch Umformen:

$\rho _{{\mathrm K}}=\rho _{1}+{\frac {F_{1}}{V_{{\mathrm K}}\cdot g}}$

Nach dieser Methode bestimmte schon Archimedes die Dichte der Krone eines Königs, der bezweifelte, dass diese wirklich aus reinem Gold bestehe (ρ_K = 19320 kg/m³).

Auf dieser Auftriebswägung von Flüssigkeiten beruhen das Aräometer (Spindel) und die Mohrsche Waage.

Weitere Methoden

Pyknometer, Dichtebestimmung von Festkörpern oder Flüssigkeiten durch Messen der verdrängten Flüssigkeitsvolumina
Isotopenmethode, Dichtebestimmung durch Strahlungsabsorption
Biegeschwinger, Dichtebestimmung, insbesondere von durchströmender Flüssigkeit, durch Schwingungsmessung
Resistograph, Dichtebestimmung von Holz über Festigkeit.
Schwebemethode, Dichtebestimmung durch Gleichgewichtsbestimmung mit Hilfe einer Schwerflüssigkeit

Eine einfache Abschätzung der Dichte lässt sich mit der Girolami-Methode erhalten.

Dichte von Lösungen

Die Summe der Massenkonzentrationen der Bestandteile einer Lösung ergibt die Dichte der Lösung, indem man die Summe der Massen der Bestandteile durch das Volumen der Lösung teilt.

$\rho = \frac{1}{V} \sum_i m_i = \frac{\sum_i \rho_i V_i}{V}$

Dabei sind die $m_{i}$ die einzelnen Teilmassen, $V_{i}$ die einzelnen Teilvolumina und V das Gesamtvolumen.

Ortsabhängige Dichte

Mit $\mathrm dm$ werde die Masse in einem gewissen Kontrollvolumen $\mathrm {d} V$ bezeichnet. Bei stetig verteilter Masse kann man einen Grenzübergang durchführen, d.h., man lässt das Kontrollvolumen immer kleiner werden und kann so die Massendichte $\rho(\mathbf x)$ durch

$\mathrm dm = \rho(\mathbf x) \,\mathrm dV$ /DD>

definieren. Die Funktion $\rho\colon\R^3 \to \R$ wird auch als Dichtefeld bezeichnet.

Für einen homogenen Körper, dessen Massendichte in seinem Inneren überall den Wert $\rho _{0}$ hat, ist die Gesamtmasse das Produkt von Dichte und Volumen , d.h., es gilt

$m = \rho_0\,V$ .

Bei inhomogenen Körpern ist die Gesamtmasse allgemeiner das Volumenintegral

$m = \int_V \rho(\mathbf x)\,\mathrm dV$

über die Massendichte.

Die Dichte ergibt sich aus den Massen der Atome, aus denen das Material besteht und aus ihren Abständen. In homogenem Material, zum Beispiel in einem Kristall, ist die Dichte überall gleich. Sie ändert sich normalerweise mit der Temperatur und bei kompressiblen Materialien (wie z.B. Gasen) auch mit dem Druck. Daher ist beispielsweise die Dichte der Atmosphäre ortsabhängig und nimmt mit der Höhe ab.

Der Kehrwert der Dichte wird spezifisches Volumen genannt und spielt vor allem in der Thermodynamik der Gase und Dämpfe eine Rolle. Das Verhältnis der Dichte eines Stoffes zur Dichte im Normzustand wird als relative Dichte bezeichnet.

In der ersten Ausgabe der DIN 1306 Dichte und Wichte; Begriffe vom August 1938 wurde die Dichte im heutigen Sinn als mittlere Dichte genormt und die ortsabhängige Dichte in einem Punkt als Dichte schlechthin definiert: „Die Dichte (ohne den Zusatz ‚mittlere‘) in einem Punkte eines Körpers ist der Grenzwert, dem die mittlere Dichte in einem den Punkt enthaltenden Volumen zustrebt, wenn man dieses so weit verkleinert denkt, dass es klein wird gegen die Abmessungen des Körpers, aber noch groß bleibt gegen die Gefügeeinheiten seines Stoffs.“ In der Ausgabe vom August 1958 wurde dann die mittlere Dichte in Dichte umbenannt mit der Erläuterung: „Masse, Gewicht und Volumen werden an einem Körper bestimmt, dessen Abmessungen groß sind gegen seine Gefügebestandteile.“

Beispiele

Die Dichte einzelner Stoffe und Materialien ist auf der jeweiligen Seite zu finden.

Material	Massendichte
Interstellare Materie	10² … 10⁹ Atome/m³ ≈ 10⁻¹³ … 10⁻⁶ g/km³
Gase	0,09 kg/m³ (Wasserstoff) … 0,18 kg/m³ (Helium) … 1,29 kg/m³ (Luft) … 1,78 kg/m³ (Argon) … 12,4 kg/m³ (Wolfram(VI)-fluorid)
Holz	200 kg/m³ … 1 200 kg/m³
Flüssigkeiten	616 kg/m³ (Isopentan) … 1000 kg/m³ (Wasser) … 1 834 kg/m³ (Schwefelsäure H₂SO₄) … 3 119 kg/m³ (Brom Br₂) … (diverse Schwerflüssigkeiten) … 13 595 kg/m³ (Quecksilber Hg)
Metalle	534 kg/m³ (Lithium) … 7874 kg/m³ (Eisen Fe) … 19 302 kg/m³ (Gold) … 22 590 kg/m³ (Osmium)
Beton	800 bis 2 000 kg/m³ (Leichtbeton) … 2 400 kg/m³ (Normalbeton) … 2 600 bis 4 500 kg/m³ (Schwerbeton)
Sterne	1 400 kg/m³ (unsere Sonne) … 1,1 · 10⁶ kg/m³ (Sterne mit Heliumbrennen) … 10¹³ kg/m³ (Kernfusion schwerer Elemente) … 10¹⁷ bis 2,5 · 10¹⁸ kg/m³ (Neutronenstern)

Dichten von Pulvern und porösen Materialien

Bei porösen Materialien muss man zwischen der Skelett- oder Reindichte, bei der die Masse auf das Volumen ohne die Poren bezogen wird, und der scheinbaren Dichte unterscheiden, die sich auf das Gesamtvolumen einschließlich der Poren bezieht. Bei Pulvern, Schüttgütern und Haufwerken hängt die scheinbare Dichte auch davon ab, ob das Material lose aufgeschüttet oder gestampft wurde. Dementsprechend unterscheidet man zwischen der Schüttdichte und der Rüttel- oder Stampfdichte. Das Verhältnis zwischen Schüttvolumen und Stampfvolumen heißt auch Hausner-Faktor.

Ausdehnungskoeffizienten

→ Hauptartikel: Ausdehnungskoeffizient

Die Veränderung der Umgebungsbedingungen führt zu einer Änderung der Dichte. Der Ausdehnungskoeffizient ist im Allgemeinen nicht konstant, sondern abhängig von den Umgebungsbedingungen, beispielsweise der Temperatur. Für zwei Temperaturen $T_{0}$ und $T_{2}$ mit $T_{2}>T_{0}$ lässt sich ein mittlerer statistischer Volumenausdehnungskoeffizient $\gamma _{\text{mittl.}}$ berechnen, aus dem sich der Quotient der beiden Dichten $\rho _{0}$ und $\rho _{2}$ berechnen lässt:

${\frac {\rho _{0}}{\rho _{2}}}=1+\gamma _{\text{mittl.}}\cdot (T_{2}-T_{0})$

Basierend auf einem Artikel in:

Wikipedia.de