Gütefaktor
Der Gütefaktor, auch Güte, Kreisgüte, Filtergüte, Schwingkreisgüte, Resonanzschärfe oder Q-Faktor genannt, ist in der Technik ein Maß für die Dämpfung bzw. den Energieverlust eines zu Schwingungen fähigen Systems (z.B. eines Schwingkreises). Eine hohe Güte eines Systems besagt, dass das System schwach gedämpft ist.
In einer zweiten Bedeutung ist der Gütefaktor ein Kennzeichen für den Energieverlust eines zweipoligen elektrischen Bauelementes oder Netzwerks.[2]
Der Kehrwert des Gütefaktors heißt in beiden Bedeutungen Verlustfaktor.
Elektrischer Schwingkreis
Definition
Der Gütefaktor
eines Resonanzkreises bei einer gegebenen Frequenz wird definiert als
mit
der gespeicherten Energie zu Beginn einer Schwingungsperiode
der Energie, die innerhalb dieser Periode in thermische Energie übergeht.
Ein Gütefaktor von 0,5, oder ein Dämpfungsgrad
von 1 oder ein Verlustfaktor von 2, entspricht dem aperiodischen
Grenzfall, bei dem es gerade keine Schwingung mehr gibt. Eine hohe
Güte erfordert also ein
deutlich über 0,5.
Reihenschaltung
In einem Reihenschwingkreis
werden ein elektrischer
Widerstand ,
eine Spule
der Induktivität
und ein Kondensator
der Kapazität
von demselben sinusförmigen Strom
mit dem Effektivwert
und der Amplitude
durchflossen. Die Resonanzfrequenz des idealen Schwingkreises und des realen
Reihenschwingkreises beträgt
mit der Resonanzkreisfrequenz
.
Die Periodendauer
beträgt
.
Eingesetzt in die Definition von
ergibt sich
Die Differenzialgleichung des Reihenschwingkreises lautet (sieheHauptartikel)
mit dem Dämpfungsgrad .
Nach Division durch
führt ein Koeffizientenvergleich auf
,
und man kommt auf eine Beziehung zwischen Dämpfungsgrad und Gütefaktor
.
Parallelschaltung
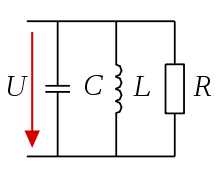
In Analogie dazu liegt in einem Parallelschwingkreis
an
dieselbe sinusförmige Spannung
an (Scheitelwert
,
Effektivwert
).
Beim realen Parallelschwingkreis liegt die Resonanzfrequenz
geringfügig niedriger als
.
Für die Berechnung der thermischen Energie, die in der Periodendauer abgegeben
wird, kann der Unterschied unbeachtet bleiben.
Bandbreite
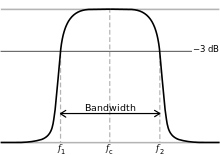
Der Gütefaktor eines Resonanzkreises ist ein Maß für die Schärfe der Resonanz. Diese wird durch die 3-dB-Bandbreite B ausgedrückt:
mit dem daraus gebildeten Gütefaktor:
Die obere Grenzfrequenz
und die untere Grenzfrequenz
sind diejenigen Frequenzen, bei denen die Spannung
bzw. der Strom
auf den
-fachen
Wert des Maximalwertes zurückgehen. An dieser Stelle ist die Leistung im
Schwingkreis nur noch halb so groß wie bei der Resonanzfrequenz des verlustlosen
Schwingkreises. Bei Darstellung des Pegels
in Abhängigkeit von der Frequenz
ist die Bandbreite gleich dem Frequenzbereich, an dessen Grenzen die Leistungswurzelgröße
um 3 dB
abnimmt. Die Grenzfrequenzen können berechnet werden aus
und
.
Sie sind mit der Resonanzfrequenz des idealen Schwingkreises verbunden durch
.
Mechanischer Schwingkreis
In der Mechanik geht man bei einem Federpendel (Masse-Feder-System) aus von den Differenzialgleichungen
.
mit der Auslenkung
aus der Ruhelage, der Masse
,
der vorzugsweise durch Reibung bestimmten Dämpfungskonstanten
,
der Federkonstanten
,
dem Dämpfungsgrad
und der Eigenkreisfrequenz
des ungedämpften Systems.
Dieselbe Definition des Gütefaktors wie beim elektrischen Schwingkreis führt auf
mit der gegenüber
leicht verminderten Eigenkreisfrequenz des schwach gedämpften Systems
Elektrisches Bauelement
Der Gütefaktor
eines linearen abstrahlungsfreien zweipoligen Netzwerkelementes oder Netzwerkes
bei sinusförmigen Vorgängen wird definiert als das Verhältnis der Beträge von Blindleistung
und Wirkleistung
oder gleichwertig als das Verhältnis der Beträge von Blindwiderstand
und Wirkwiderstand
.
.
Der Gütefaktor ist ein Maß für – gewöhnlich unerwünschte – Verluste, insbesondere in einem Kondensator oder einer Spule. Beispielsweise ist die Spulengüte
Diese Gleichung ähnlich der entsprechenden Gleichung beim Reihenschwingkreis,
gilt aber für beliebige Frequenz
und nicht bei einer (gar nicht vorhandenen) Resonanzfrequenz
.
Eine hohe Spulengüte ist erforderlich, wenn in einem Schwingkreis eine geringe
Bandbreite angestrebt wird.
Der Gütefaktor ist bei Netzwerk(element)en zugleich der Kotangens des Verlustwinkels.
Beispiele
In der folgenden Tabelle sind einige Größenordnungen von Gütefaktoren bei verschiedenen schwingenden Systemen angegeben.
| System | Gütefaktor Q |
|---|---|
| Aperiodischer Grenzfall | |
| Elektrodynamischer Lautsprecher | typ. |
| Elektrischer Schwingkreis | |
| Pendeluhr | |
| Schwingungstilger | |
| Schwingquarz 10 MHz | |
| Frequenzstabilisierter Laser | |
| Supraleitender Hohlraumresonator | |
| Cäsium-Atomuhr | |
| Mößbauer-Effekt bei Gammastrahlung |
Literatur
- Bernd Girod, Rudolf Rabenstein, Alexander Stenger: Einführung in die Systemtheorie. 4. Auflage. Teubner, Wiesbaden 2007, ISBN 978-3-8351-0176-0.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.08. 2023