Verlustfaktor

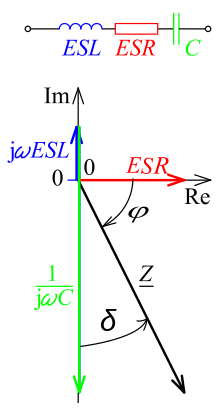
Ersatzschaltbild eines Kondensators bei höherer Frequenz (oben);
Darstellung des Verlustwinkels δ und der Impedanz Z als Zeigerdiagramm in der komplexen Ebene (unten)

Der Verlustfaktor (engl.: dissipation factor, abgekürzt DF) beschreibt bei physikalischen Schwingungen unterschiedlicher Natur das Verhältnis des verlustbehafteten Realteils zum verlustfreien Imaginärteil einer komplexen Größe. Der Verlustfaktor ist gleich dem Tangens des Verlustwinkels $\delta$ zwischen der komplexen Größe und ihrem Imaginärteil. Praktische Anwendung findet er unter anderem in der Elektrotechnik und der Rheologie.

Anwendungen

Elektrische Bauelemente

Der Verlustfaktor gibt an, wie groß die Verluste in elektrischen Bauteilen wie Drosseln und Kondensatoren oder bei der Ausbreitung elektromagnetischer Wellen in Materie (z.B. Luft) sind. Mit „Verlust“ ist hierbei die Energie gemeint, die elektrisch oder elektromagnetisch umgewandelt wird und sich beispielsweise in Wärme umwandelt (Dissipation). Durch diese Verluste wird die elektromagnetische Welle gedämpft.

Zur genaueren Darstellung des Verlustfaktors wird ein Kondensator betrachtet, der an eine Spannungsquelle mit sinusförmigem Spannungsverlauf über der Zeit angeschlossen ist. An einem solchen Kondensator tritt eine Phasenverschiebung $\varphi$ zwischen Spannung und Strom auf: Ein idealer Kondensator, der keinerlei Verluste aufweist, hat eine Phasenverschiebung von $\varphi =90^{\circ }={\tfrac {\pi }{2}}$ (Bogenmaß). Bei einem realen Kondensator, der Verluste hat, ist die Phasenverschiebung $\varphi$ um den Verlustwinkel $\delta$ kleiner als $90^{\circ }$ :

$\varphi = 90^\circ - \delta \Leftrightarrow \delta = 90^\circ - \varphi$

Gemäß der komplexen Wechselstromrechnung in der Elektrotechnik ist der Verlustfaktor definiert als Tangens dieses Verlustwinkels:

$DF = \tan \delta$

Schwingkreis

Als Verlustfaktor d (Dämpfung; auf Englisch dissipation factor DF) wird auch der Kehrwert des Gütefaktors Q bei Schwingkreisen und Filtern bezeichnet:

$d = \frac{1}{Q}$ .

Materialdämpfung

Bei der inneren Dämpfung von Materialien bezeichnet der Verlustfaktor µ die Fähigkeit des Materials, Vibrationen und Körperschall zu dämpfen. Von Relevanz ist dies etwa im Fahrzeug- und Maschinenbau sowie in der Bauakustik und Baudynamik.

Rheologie

Siehe auch: Komplexer Schubmodul

In der Rheologie bezeichnet der Verlustfaktor $\tan \delta$ das Verhältnis zwischen Verlustmodul G'' (Imaginärteil) und Speichermodul (Realteil):

$\tan \delta = \frac{G''}{G'}$

je höher der Verlustfaktor, desto mehr nähert sich das Verhalten einer Probe dem einer ideal-viskosen Flüssigkeit mit newtonschem Fließverhalten an

(Beispiel Wasser: Speichermodul $G'=0\Leftrightarrow \cos \delta =0\Leftrightarrow \delta =90^{\circ }\Rightarrow \tan \delta \to \infty$ )

je niedriger der Verlustfaktor, desto mehr entspricht das Verhalten einer Probe dem eines ideal-elastischen Festkörpers

(Beispiel Stahl: Verlustmodul $G''=0\Leftrightarrow \sin \delta =0\Leftrightarrow \delta =0^{\circ }\Rightarrow \tan \delta =0$ ).

Basierend auf einem Artikel in:

Wikipedia.de