Fachwerk
Ein Fachwerk ist ein Stabwerk, dessen Stäbe ausschließlich auf Normalkräfte beansprucht werden.
Der Begriff Fachwerk leitet sich vermutlich vom Mittelhochdeutschen vach oder fah für in Felder geteilte Fläche und Geflecht ab. Beim Fachwerkhaus traf beides zu: Die Wandfläche wurde in mit Rohrgeflecht gefüllte Felder geteilt.
In einem idealen Fachwerk treten keine Biegemomente auf. Knoten werden in realen Fachwerken oftmals verbindungstechnisch insofern einfachst (biegeweich) gestaltet, dass Biegemomente übertragbar wären, jedoch sind die Stäbe so biegeweich, dass die Momente eine unwesentliche Größenordnung haben, welche in realen Fachwerken in der statischen Berechnung üblicherweise berücksichtigt werden müssen. Die funktionell mögliche und früher auch angewendete gelenkige Verbindung mit z. B. Bolzen und Hülse wurde aus Kostengründen fallen gelassen.
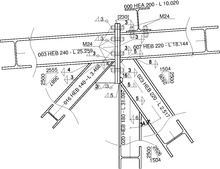
Schweiß- und Schraub-Verbindungen
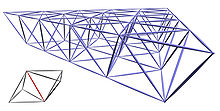
Grundzellen (Tetraeder) aus sechs Stäben
Anwendungen
Bauwesen
Konstruktionen aus Fachwerken haben im Allgemeinen im Verhältnis zu anderen üblichen Bauweisen für ihre Tragfähigkeit ein geringes Eigengewicht. Nachteilig kann sich ihr großes Volumen auswirken (Beispiel: optisch stark in Erscheinung tretende Fachwerkbrücken). Ihre Erdbebensicherheit ist hoch.
Räumliche Gebäude-Fachwerke gibt es als Fassaden, Dächer (inkl. Vordächer und Hallendächer) und Kuppeln. Weitere Anwendungen sind Fachwerkbrücken, Kräne (Portalkräne, Kranbrücken, Turmkräne, Wippkräne u. a.), Masten (Hochspannungsmasten, Oberleitungsmasten, Telefonmasten, Windkraftmasten) und Aussichtstürme.
- Bauwesen-Fachwerke, schematisch
-
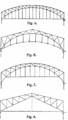Für Brücken und Dächer -
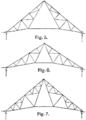Für Dächer (Polonceaubinder) -
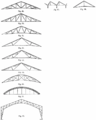Für Dächer und Hallen (mit Masten) -
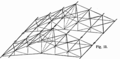Ebene Dachfachwerke die zu einem räumlichen Stabwerk zusammengefügt sind (die Sparren werden hauptsächlich auf Biegung beansprucht, deshalb ist es kein Räumliches Fachwerk)
Fahrzeugbau
Im Automobilbau und Motorradbau werden räumliche Fachwerke für Fahrgestelle als sogenannte Gitterrahmen verwendet. Sie enthalten aber oft nicht ausschließlich Stabdreiecke, was insbesondere auf die Motorradrahmenutrifft. Dabei handelt es sich um Mischformen aus allgemeinem, biegesteifem Stabwerk und Fachwerk.
Bei Flugzeugen wurde historisch der ganze Rumpf mitsamt Flügeln aus (Holz-) Fachwerk gefertigt und bespannt, etwa beim DFS 230, einem Lastensegler mit Flugzeugrumpf aus einem geschweißten Stahlrohrfachwerk mit Stoffbespannung. Auch Starrluftschiffe wurden – im Unterschied zu aufgepumpten Prallluftschiffen – mit Fachwerk-Stützkonstruktionen aufgebaut.
Mechanik der Fachwerke
Die Untersuchung der Gebrauchsfähigkeit (Festigkeit und elastische Verformung) von Fachwerken erfolgt mit Hilfe der Festigkeits- und Verformungslehre, die in ihrer Anwendung bei Tragwerken als Baustatik bezeichnet wird.
Statische Bestimmtheit: Abzählkriterien
Dass ein Fachwerk statisch bestimmt ist, ist eine bei seiner Untersuchung zuerst zu beantwortende Frage. Ein statisch unterbestimmtes Fachwerk scheidet aus, da es auf seinen Fundamenten oder in sich beweglich wäre. Statisch überbestimmte Fachwerke haben zu viele Stäbe, was dem Prinzip Leichtbau widerspricht. Sie sind aber stabil, haben lediglich den Nachteil, dass der Untersuchungsaufwand größer wird. Thermische Ausdehnungen und Versetzungen der Fundamente können bei ihnen sekundäre (bezüglich eigentlichem Gebrauch zusätzliche) Beanspruchungen bewirken.
Die Frage wird prinzipiell durch Auswerten der Gleichgewichtsbedingungen (Summe aller Kräfte bzw. Drehmomente ist Null) beantwortet. Als vereinfachte Bestimmungsmethode wurden aus ihnen die sogenannten Abzählkriterien entwickelt. Für Grenzfälle liefern sie aber nicht immer das richtige Ergebnis, was wegen ihrer schematischen Anwendung zudem nicht erkennbar ist. Die Abzählkriterien sind nur eine notwendige, aber nicht hinreichende Bedingung für den Nachweis statischer Bestimmtheit.
Erfahrene Fachwerkkonstrukteure benutzen deshalb zusätzliche, sogenannte Abbau- bzw. Aufbaukriterien (was passiert, wenn ein Stab entfernt oder hinzugefügt wird?). Die sichere Antwort für jeden Fall und für Ungeübte folgt nur aus der Arbeit mit den Gleichgewichtsbedingungen.
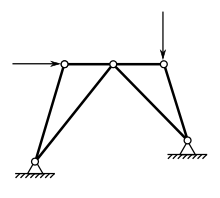
Für ebene Fachwerke wird folgende Formel verwendet:
Hierbei ist
die Summe der in den Auflagerdrehgelenken unterbundenen Bewegungsmöglichkeiten
(Wertigkeiten der Auflager),
die Anzahl der Stäbe,
die Anzahl der Drehgelenke (Auflager + Verbindungen).
Beispiel: nebenstehend abgebildetes Fachwerk
⇐ das
nebenstehend abgebildete Fachwerk ist statisch bestimmt.
Für räumliche Fachwerke wird folgende Formel verwendet:
Ideales und reales Fachwerk
Dieses Begriffspaar wird in vielen Arbeiten zur Untersuchung von Fachwerken verwendet.
Ideales Fachwerk
Das ideale Fachwerk ist Synonym dafür, dass bei der Berechnung üblicherweise schwach wirkende Effekte mehr oder weniger vernachlässigt werden, dient aber missverständlicherweise und in einem Teilaspekt (s. u.: zweites Merkmal) angewendet auch als Definition für das Fachwerk an sich.
Notwendige Kriterien die ein Fachwerk erfüllen muss:
- Alle Fachwerkstäbe sind perfekt gerade.
- Sie sind an ihren Enden mit reibungsfreien Gelenken miteinander frei drehbar verbunden.
- Die Achsen (und somit auch die Wirkungslinien der Stabnormalkräfte) der in einem Knoten verbundenen Stäbe schneiden sich in einem Punkt (Knotenpunkt).
- alle äußeren Belastungen, sind ausschließlich Einzelkräfte die ausschließlich an Knotenpunkten angreifen (so genannte Knotenkräfte)
Aus diesen Kriterien folgt, dass in den Stäben ausschließlich Normalkräfte herrschen. An keinem Stab wirke von außen eine Querkraft- oder Biegemomentbelastung. Die Stabgewichte seien vernachlässigbar klein.
Weil in der Praxis außer in den äußeren Anschlüssen (Lagern) selten Verbindungen vorkommen die große Rotationen zulassen. Aufgrund der kleinen Winkeländerungen in den Knoten und der Biegeweichheit des Verbindungen und der Einzelstäbe, spricht man in der Modellbildung dennoch von (nicht reibungsfreien) Gelenken, die in einer ersten statischen Modellbildung als (reibungsfreie) Vollgelenke idealisiert werden.
Reales Fachwerk
In einem realen Fachwerk (ein gebautes Fachwerk) treffen die idealisierten Merkmale mehr oder weniger nicht zu.
- Durch Stäbe, die die Knoten exzentrisch treffen,
- durch die Eigengewichte der Stäbe (insbesondere der nicht vertikalen),
- durch Stabbelastungen außerhalb der Knoten und
- durch die Reibung in den tatsächlich als Auflager existierenden Gelenken treten Nebenspannungen auf, die die Knoten verdrehen, aber i. d. R. „sehr viel kleiner als die Spannungen aus der Haupttragwirkung über Normalkräfte“ sind.
Einfache ebene Fachwerke
Ein einfaches Fachwerk ist eine bestimmte Sonderform eines idealen Fachwerks und besteht ausschließlich aus Stabdreiecken. „Ein einfaches ebenes Fachwerk besteht allein aus Stabdreiecken. Es wird gebildet, indem man, ausgehend von einem Stab, jeweils durch Anfügen von zwei Stäben einen neuen Knoten bildet, so dass ein Stabdreieck entsteht.“
Berechnungsverfahren für Fachwerke
Knotenpunktverfahren (Rundschnittverfahren)
Mit dem Knotenpunktverfahren lassen sich die Stabkräfte durch Aufstellen eines Gleichungssystems ermitteln. Für jeden Knoten eines 2-D-Fachwerkes werden die je maximal zwei linear unabhängige Gleichgewichtsbedingungen – z.B. die Summe der Kräfte in x- und in y-Richtung muss Null sein – ermittelt. Dadurch ergibt sich ein Gleichungssystem, das bei statischer Bestimmtheit des Fachwerkes gelöst werden kann.
Im dreidimensionalen Fall können jeweils maximal drei linear unabhängige Gleichungen aufgestellt werden.
Rittersches Schnittverfahren
Das Rittersche Schnittverfahren dient zur Berechnung von Stabnormalkräften im Fachwerk. Somit können pro Schnitt im Zweidimensionalen maximal drei Stabkräfte oder im Dreidimensionalen maximal sechs Stabkräfte berechnet werden.
Stabtauschverfahren
Das Hennebergsche Stabtauschverfahren wird bei nicht einfachen Fachwerken angewandt.
Cremonaplan
Der Cremonaplan dient bei statisch bestimmten Fachwerken der zeichnerischen Bestimmung der Stabkräfte.
Raumfachwerk
Raumfachwerke unterscheiden sich von räumlichen Stabwerken dadurch, dass sie auch ohne biegefeste Verbindungen der Stäbe untereinander stabil sind. Sie erfüllen damit das Bildungsgesetz für räumliche Fachwerke. Die Räumlichkeit der Fachwerke kann entweder durch Anordnung der Stäbe in mehreren Lagen (Untergurt, Diagonalen, Obergurt), oder/und durch Anordnung der Stäbe im Raum erfolgen. Im ersten Fall erzeugt man ein ebenes Raumfachwerk, im zweiten Fall ein gestuftes oder gekrümmtes Raumfachwerk, das im Sonderfall (z.B. bei einer Kuppel) auch einlagig sein kann. Ein klassisches Beispiel des räumlichen gekrümmten, aber im Prinzip ebenen Fachwerkes ist die geodätische Kuppel.
Die Verbindung der Stäbe erfolgt im Allgemeinen mit Knotenteilen, die massiv (Kugeln, Zylinder) oder aufgelöst (Scheiben) ausgeführt werden können.
- Beispiele
-
Computergrafik eines Mero-Raumfachwerkknotens. -
Blick in das RFW von Air Shard Daniel Libeskinds Imperial War Museum North -
Raumfachwerk am Flughafen Stansted Airport -
Unregelmäßiges Raumfachwerk des Water Cube in Peking -
Raumfachwerk der Thalkirchner Brücke in München -
Geodätische Kuppel: Gewächshaus im Botanischen Garten Düsseldorf
Geometrie
Die Geometrie der Stabanordnung spielt eine wesentliche Rolle beim Entwurf von Raumfachwerken. Die ebenen und gestuften Raumfachwerke lassen sich aus einer Kombination (Komposition) von Tetraeder und (Halb-) Oktaeder ableiten, seltener aus dem Hexaeder (Kubus). Die Raumfachwerke für Kuppeln können aus dem Dodekaeder und Ikosaeder abgeleitet werden. Die fünf genannten Polyeder bilden die platonischen Körper.
Die Geometrie von Raumfachwerken auf Freiformflächen, insbesondere solche auf NURBS (Non Uniform Rational B-Spline-Flächen), erfordert den Einsatz von CAD-Spezialprogrammen, die die Netzgenerierung auf diesen Flächen zulassen.
Planung und Fertigung
Durch die von Computern unterstützte Planung und Fertigung können beliebige Konfigurationen realisiert werden. Trotzdem stellt die Orientierung der Verbindungsknoten ein besonderes Problem dar, um Knotengröße und Fräsarbeit insbesondere bei Freiformflächen mit direkt aufliegender Glaseindeckung zu minimieren.
Material
Als Material stehen Rohre (runde und rechteckige), Profilträger (I-, L-, U-, T-, Z-Profile) aus Stahl, Aluminium, Edelstahl und in Sonderkonstruktionen auch aus kohlenstofffaserverstärktem Kunststoff oder Holz (Bretter, Bohlen, Kanthölzer) zur Auswahl. Für die Knoten kommen u.a. Schmiede- und Gussteile aus Stahl, sowie Drehteile aus Aluminium oder Edelstahl zum Einsatz.
Wikipedia.de
© biancahoegel.de
Datum der letzten Änderung: Jena, den: 18.12. 2020