
Nyquist-Diagramm
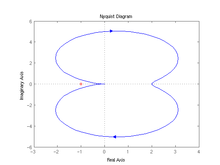
Ein Nyquist-Diagramm, auch als Nyquist-Graph oder Nyquist-Plot bezeichnet, stellt die Ortskurve der Ausgangsgröße eines Regelkreises mit der Frequenz als Parameter dar. Es wird in der Regelungstechnik, Verstärkerkonstruktion und Signalaufbereitung verwendet, um die Stabilität eines Systems mit Rückkopplung zu beschreiben. Es ist nach dem schwedisch-amerikanischen Physiker Harry Nyquist benannt.
Das Nyquist-Diagramm ist ein parametrischer Funktionsgraph einer komplexwertigen Funktion, im Normalfall einer Fourier-Übertragungsfunktion eines LZI-Systems, in der komplexen Ebene. Es erfüllt also einen ähnlichen Zweck wie das Bode-Diagramm, nämlich die Darstellung von Funktionen mit komplexwertigen Ausgabewerten:
Im Gegensatz zum Bode-Diagramm wird beim Nyquist-Diagramm Betrag und Phase in
einem einzigen Diagramm dargestellt, nämlich indem man den Real- und
Imaginärteil des Ausgabewertes direkt in die komplexe Zahlenebene zeichnet. Eine
Linie entsteht, indem man für den Funktionsparameter
alle möglichen Werte einsetzt. Alternativ kann auch Betrag und Phase des
Ausgabewertes eingetragen werden, wobei der Bezug zu Frequenz- und Phasengang
des Bode-Diagramms nahe liegt. Ein wesentlicher Unterschied zum Bode-Diagramm
besteht darin, dass beim Nyquist-Diagramm häufig keine Werte des
Funktionsparameters
eingetragen werden, weshalb anhand des Graphen keine Aussage über
Knickfrequenzen u.Ä. gemacht werden können.
Der Nutzen von Nyquist-Diagrammen besteht darin, dass die Stabilität des rückgekoppelten Systems leicht vorausgesagt werden kann, indem man diese Kurve darstellt. Dabei können Stabilität und andere Eigenschaften verbessert werden, indem man den Plot graphisch verändert. Siehe: Stabilitätskriterium von Nyquist
Nyquist- und ähnliche Diagramme sind klassische Methoden zur Voraussage der Stabilität einer Schaltung. Sie sind zwar durch computergestützte mathematische Werkzeuge in den letzten Jahren ergänzt oder verdrängt worden, aber sie sind besonders geeignet, dem Entwickler ein intuitives Gefühl für das Schaltungsverhalten zu geben.
Experimentelles Bestimmen eines Nyquistdiagramms
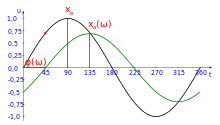
Man kann sich folgenden Experimentaufbau vorstellen: Eine Schaltung, als Beispiel die Reihenschaltung eines Widerstands und eines Kondensators (Tiefpass/RC-Glied), wird von einem Funktionsgenerator mit einer Sinusspannung beaufschlagt. Mit einem Oszilloskop werden die Eingangsspannung und die Spannung am Kondensator (als Ausgangsspannung) gemessen. Am Eingang gilt:
Die Spannung am Ausgang hat eine andere Amplitude und eine Phasenverschiebung gegenüber der am Eingang:
Es sind:
: Kreisfrequenz der Eingangsspannung,
: Augenblickswert der Eingangsspannung,
: Augenblickswert der Ausgangsspannung,
: Amplitude (Betrag) der Eingangsspannung,
: Amplitude (Betrag) der Ausgangsspannung,
: Phasenverschiebung,
: Zeit.
Wenn man zu jedem
die Parameter
und
ermittelt, ergibt sich der komplexe
Frequenzgang zu:
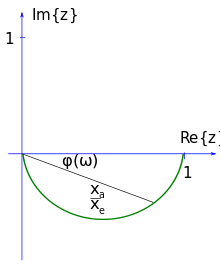
In dem zweiten Bild ist das Nyquistdiagramm der als Beispiel gewählten
RC-Schaltung (ein PT1-Glied)
dargestellt. Die mit
beschriftete Linie entspricht einem von
abhängigen Funktionswert in der komplexen
Zahlenebene. Die Ortskurve
verläuft ausgehend von 1 mit steigendem
zum Ursprung und bildet dabei einen Halbkreis. Die Amplitude wird mit steigendem
kleiner, daher handelt es sich um einen Tiefpass.
Berechnen eines Nyquistdiagramms
Als Beispiel für die Berechnung des Nyqistdiagramms nimmt man ein einfaches
PT1-Glied. Um auf das
Beispiel mit dem Widerstand und dem Kondensator zurückzukommen, ist
und
.
Die Komplexe Zahl im Nenner lässt sich durch konjugiert komplexes Erweitern herauskürzen:
dann erhält man Real- und Imaginärteil:
,
Damit errechnet sich Betrag und Phase
Die Extremwerte ergeben sich folgendermaßen:
Es ergibt sich ein Halbkreis wie in der obigen Grafik unter Experimentelles Bestimmen eines Nyquistdiagramms.
Zeichnen eines Nyquistdiagramms
Zum Zeichnen einer Übertragungsfunktion (Fourier-Frequenzbereich):
Das Zeichnen der Funktion erfolgt nun durch bloßes Einsetzen von Werten für
Parameter ,
was komplexe Zahlen ergibt, welche dann ins Diagramm eingetragen und verbunden
werden. Um ein breites Spektrum abzudecken, sind logarithmisch ansteigende Werte
für
sowie Grenzwertbetrachtungen
für
von Nutzen. Außerdem ist es nützlich, die Achsenschnittstellen zu berechnen,
indem man die Real- bzw. Imaginärteile gleich Null setzt und nach
umformt.
Z.B.:
berechnen und eintragen.
Hinweis: Die Tangente des Nyquist-Pfades im Punkt
verläuft stets senkrecht zum Realteil.
Vereinfachte Skizze der Nyquist-Ortskurve
Eine schnelle Skizze der Ortskurve kann in bestimmten Fällen auch mit einem vereinfachten Verfahren erfolgen. Dabei ist die Übertragungsfunktion in folgender Form gegeben:
Zusätzlich müssen folgende Voraussetzungen vorliegen: ,
,
und die Pole und Nullstellen dürfen nicht rechts der imaginären Achse liegen.
Der Beginn der Ortskurve für
wird unter einem Winkel von
(von der Realachse aus gemessen) gezeichnet, und die Ortskurve dreht im
Uhrzeigersinn weiter, bis
für
.
Wenn
ist, dreht die Ortskurve monoton, und es treten keine Änderungen in der Krümmung
der Ortskurve auf. Wegen
endet die Ortskurve im Ursprung.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.09. 2023