
Geringter Raum
Ein geringter Raum ist ein Konstrukt aus den mathematischen Teilgebieten der algebraischen Geometrie und der Funktionentheorie. Ein geringter Raum besteht aus einem topologischen Raum und einer Menge kommutativer Ringe, deren Elemente man als Funktionen auf den offenen Mengen des Raumes verstehen kann.
Definition
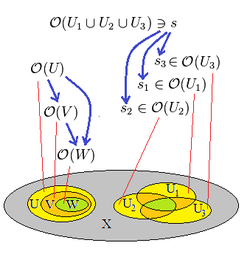
Ein geringter Raum ist ein topologischer Raum
zusammen mit einer Garbe
kommutativer Ringe auf
,
das heißt:
- Für jede offene Menge
ist ein Ring
gegeben, den man auch als
schreibt.
- Sind
offene Teilmengen von
, so gibt es einen Ringhomomorphismus
, so dass
- Für offene Mengen
gilt
,
- Für jede offene Menge
gilt
,
- Für offene Mengen
- und
erfüllt die Garbenbedingungen: Für jede offene Menge
und jede offene Überdeckung
von
, das heißt
, und für Elemente
mit
für alle
gibt es genau ein
mit
für alle
.
Die Homomorphismen
nennt man Restriktionen, da es sich in vielen Anwendungen tatsächlich um
Einschränkungen von Abbildungen handelt, wie in den untenstehenden Beispielen
klar werden wird. Sind die Garbenbedingungen nicht erfüllt, so liegt nur eine Prägarbe
von Ringen vor. Hat man es mit mehreren geringten Räumen zu tun, so kann man zur
besseren Unterscheidung
schreiben, um die Zugehörigkeit zum topologischen Raum deutlich zu machen.
Man kann obige Definition auf eine topologische
Basis einschränken, indem die Ringe
und Restriktionen
nur für offene Mengen aus der topologischen Basis erklärt und obige Bedingungen
nur für Basismengen gefordert werden. Man erhält daraus einen geringten Raum im
Sinne obiger Definition, indem man für beliebige offene Mengen
den Ring
als projektiven
Limes der
mit
und
aus der gegebenen topologischen Basis definiert.
Sind alle auftretenden Halme
lokal, so spricht man von
einem lokalen geringten Raum. Dieser Fall ist in der algebraischen
Geometrie von großer Bedeutung, wie in den Beispielen gezeigt wird.
Beispiele
- Es sei
ein topologischer Raum und für jede offene Menge
sei
der Ring der stetigen Funktionen
sowie
die Einschränkungsabbildung
. Dann ist
ein geringter Raum, man nennt ihn die Garbe der Keime stetiger Funktionen.
- Ein wichtiges Beispiel aus der algebraischen Geometrie ist der wie folgt
definierte lokal geringte Raum über dem Spektrum
eines Ringes
.
- Die Mengen
bilden eine topologische Basis von
, wobei
die nicht nilpotenten Elemente durchläuft; für nilpotente Elemente ist
.
sei die Lokalisierung nach
.
- Ist
, so gibt es ein
mit
für ein
. Dann ist
wohldefiniert, und erfüllt die Bedingungen eines geringten Raumes.
- Die Mengen
- Diesen geringten Raum nennt man ein affines Schema. Da die Ringe
lokal sind, liegt ein lokal geringter Raum vor.
- Geringte Räume spielen auch in der Funktionentheorie
mehrerer Veränderlicher eine wichtige Rolle. Ist
ein Gebiet, so definiert man
als den Ring der holomorphen Funktionen
. Im unten angegebenen Lehrbuch verlangen die Autoren von einem geringten Raum
zusätzlich, dass
hausdorffsch ist und
in der Garbe der Keime stetiger Funktionen enthalten ist. Dort wird der Begriff des geringten Raumes also enger gefasst, ebenso in der Theorie der riemannschen Flächen.
Einschränkungen
Ist
ein geringter Raum und
offen, so erhält man einen geringten Raum
,
wenn man für jede offene Menge
(einer topologischen Basis) von
festlegt, dass
,
denn
ist ja auch eine offene Menge von
.
Man nennt
die Einschränkung von
auf
.
Morphismen zwischen geringten Räumen
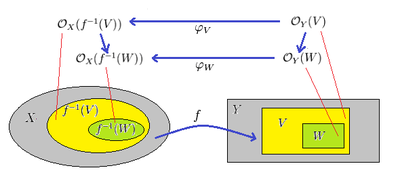
Ein Morphismus zwischen geringten Räumen
und
ist ein Paar
bestehend aus einer stetigen Abbildung
und einer Familie
,
wobei jedes
ein Ringhomomorphismus ist und für offene Mengen
in
das Diagramm
kommutativ ist, wobei die Restriktionen in beiden Garben mit
bezeichnet sind. Man sagt dafür kurz, dass die Ringhomomorphismen
mit den Restriktionen verträglich sind.
In der Kategorie der lokal geringten Räume verlangt man zusätzlich, dass die
Ringhomomorphismen
lokal sind, das heißt das maximale Ideal von
in das maximale Ideal von
abbilden.
Mit diesen Morphismen erhalten wir die Kategorie geringter Räume. Man kann
daher von isomorphen geringten Räumen sprechen. Das ist für manche
Begriffsbildungen sehr wichtig. So definiert man ein Schema
als einen geringten Raum ,
in dem jeder Punkt des topologischen Raumes eine offene Umgebung besitzt, so
dass die Einschränkung auf diese Umgebung isomorph zu einem affinen Schema ist.
Ganz ähnlich definiert man einen analytischen
Raum als einen geringten Raum, in dem jeder Punkt eine Umgebung besitzt, so
dass die Einschränkung darauf isomorph zu einem geringten Raum holomorpher
Funktionen auf einer komplexen
Mannigfaltigkeit im
ist.
Modulgarben
Ist
ein geringter Raum, so ist ein
-Modul
eine Garbe
abelscher Gruppen über
,
so dass jede abelsche Gruppe
die Struktur eines
-Moduls
trägt und die Restriktionen
der Garbe
Modulmorphismen sind, das heißt
für alle offenen Mengen
,
Ringlemente
und Modulelemente
.
Diese Objekte, die man auch Modulgarben
nennt, werden in der algebraischen Geometrie und Funktionentheorie untersucht,
wobei die kohärenten Garben eine wichtige Rolle spielen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 20.09. 2019