
Polylogarithmus
Der Polylogarithmus ist eine spezielle Funktion, die durch die Reihe
definiert ist. Für
geht der Polylogarithmus in den gewöhnlichen Logarithmus
über:
In den Fällen
und
spricht man entsprechend von Dilogarithmus
bzw. Trilogarithmus.
Die Definition gilt für komplexe
und
mit
.
Durch analytische
Fortsetzung lässt sich diese Definition auf weitere
ausdehnen.
In den wichtigsten Anwendungsfällen ist
eine natürliche
Zahl. Für diese Fälle kann man den Polylogarithmus rekursiv durch
definieren, wonach der Dilogarithmus ein Integral des Logarithmus ist, der
Trilogarithmus ein Integral des Dilogarithmus und so fort. Für negative
ganzzahlige Werte von
lässt sich der Polylogarithmus durch rationale
Funktionen ausdrücken.
Der Polylogarithmus taucht beispielsweise im Zusammenhang mit der Fermi-Dirac-Verteilung
und der Bose-Einstein-Verteilung
auf. Zudem kann mit ihm im hexadezimalen Zahlensystem eine beliebige Stelle von
polylogarithmischen
Konstanten (z.B. )
einzeln berechnet werden.
Funktionswerte und Rekursionen
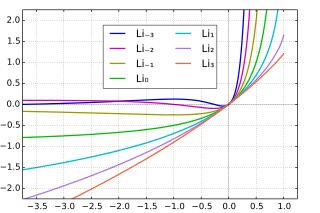
Einige explizite Funktionsterme für spezielle ganzzahlige Werte von :
Formal kann man
mit der (für alle
divergierenden) Reihe
definieren. Obwohl diese Reihe nicht konvergiert, kann diese Definition zum
Beweis von Funktionalgleichungen (im Ring der formal definierten Laurent-Reihen) verwendet
werden.
Für alle ganzzahligen nichtpositiven Werte von
kann der Polylogarithmus als Quotient von Polynomen geschrieben werden. In
diesen Fällen ist er also eine rationale
Funktion. Für die drei kleinsten positiven Werte von
sind im Folgenden die Funktionswerte an der Stelle
angegeben:
ist dabei die Riemannsche
Zetafunktion. Für größeres
sind keine derartigen Formeln bekannt.
Es gilt
und
mit der dirichletschen
-Funktion.
 |
 |
 |
 |
 |
 |
 | |
Ableitung
Die Ableitung der Polylogarithmen sind wieder Polylogarithmen:
Integraldarstellung
Der Polylogarithmus lässt sich für alle komplexen
durch
mit Hilfe des Integralausdrucks für die Lerchsche
Zeta-Funktion darstellen. Dabei ist
die unvollständige
Gammafunktion der unteren Grenze.
Verallgemeinerungen
Mehrdimensionale Polylogarithmen
Die mehrdimensionalen Polylogarithmen sind folgendermaßen definiert:
Lerchsche Zeta-Funktion
Der Polylogarithmus ist ein Spezialfall der transzendenten Lerchschen Zeta-Funktion:
Nielsens verallgemeinerte Polylogarithmen
Nielsen fand folgende Verallgemeinerung für den Polylogarithmus:
Es gilt:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.12. 2021