
Projektives Objekt
Im mathematischen Gebiet der Kategorientheorie sind projektive Objekte eine Verallgemeinerung des Begriffs der Freiheit in der Algebra.
Definition
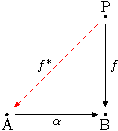
Ein Objekt P einer Kategorie C heißt projektiv, wenn es
zu jedem Epimorphismus
und jedem
ein
gibt, so dass
ist. Das heißt nebenstehendes Diagramm ist kommutativ. Also ist
genau dann projektiv, wenn für alle Epimorphismen
die induzierte Abbildung
surjektiv ist.
Beispiele
- Jedes Anfangsobjekt in einer Kategorie ist projektiv.
- In der Kategorie der Mengen Me ist jedes Objekt projektiv. Dies ist eine Folge des Auswahlaxioms.
- Das Koprodukt projektiver Objekte ist projektiv.
- Projektive Gruppen sind genau die freien Gruppen.
Eigenschaften
Ist in der Kategorie
jedes Objekt Quotient eines projektiven Objektes, d.h. gibt es zu jedem
Objekt
einen Epimorphismus
,
in dem
projektiv ist, so sagt man auch,
besitze genügend projektive Objekte. Diese Eigenschaft spielt eine Rolle
im Zusammenhang mit abgeleiteten
Funktoren. Beispielsweise besitzt die Kategorie der Gruppen genügend
projektive Objekte, weil jede Gruppe Quotient einer freien Gruppe ist
(Darstellung durch Erzeugende und Relationen).
Projektiver Modul
In der Kategorie der Moduln kann man genaueres über projektive Moduln sagen.
Für einen Modul
sind folgende Aussagen äquivalent.
ist projektiv.
- Zu jedem Epimorphismus
gibt es
, so dass
gilt. Das heißt jeder Epimorphismus mit Ziel
ist eine Retraktion.
- Jeder Epimorphismus
zerfällt. Das heißt
ist direkter Summand in
.
ist isomorph zu einem direkten Summanden eines freien Moduls.
- Der Funktor
ist exakt.
Die direkte Summe einer Familie
von Moduln ist genau dann projektiv, wenn jedes
projektiv ist. Insbesondere ist jeder direkte Summand eines projektiven Moduls
projektiv. Das Produkt projektiver Moduln ist im Allgemeinen keineswegs projektiv. So ist
beispielsweise
nicht projektiv.
Beispiele projektiver Moduln
- Jeder Ring
ist projektiv als
-Modul. Jeder freie Modul ist deshalb projektiv.
- Projektive abelsche Gruppen sind genau die freien abelschen Gruppen. Achtung: freie abelsche Gruppen sind i.a. keine freien Gruppen.
- Allgemeiner ist über jedem Hauptidealring jeder projektive Modul frei.
- Gebrochene Ideale in einem Dedekindring sind projektiv, aber im Allgemeinen nicht frei.
- Ein endlich erzeugter Modul über einem noetherschen Ring ist genau dann projektiv, wenn die zugehörige Modulgarbe lokal frei ist.
Dualbasislemma
Ein Modul
werde erzeugt von
.
Der Modul
ist genau dann projektiv, wenn es eine Familie
von Homomorphismen aus dem Dualraum
gibt mit:
- Für jedes
ist
nur für endlich viele
.
- Für jedes
ist
.
Folgerungen aus dem Dualbasislemma
- Für jeden Rechtsmodul
ist
ein Linksmodul über dem Ring
. Dieser Modul heißt der zu
duale Modul. Der Modul
ist wieder ein Rechtsmodul. Man hat den natürlichen Homomorphismus
. Ist
projektiv, so ist
injektiv.
- Ist
projektiv und endlich erzeugt, so ist
ein Isomorphismus. Man sagt
ist reflexiv.
Siehe auch
- Der duale Begriff ist der des injektiven Objektes.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.11. 2020