U(1)

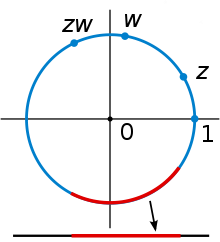
In Physik und Mathematik ist die Gruppe U(1) die einfachste kompakte Lie-Gruppe. Mathematisch handelt sich um den Einheitskreis der komplexen Zahlenebene mit der durch die Multiplikation der komplexen Zahlen gegebenen Gruppenoperation.

Sie findet unter anderem im Standardmodell der Elementarteilchenphysik Verwendung.

Das Produkt von $z=e^{i\theta _{1}}$ und $w=e^{i\theta _{2}}$ ist $zw=e^{i(\theta _{1}+\theta _{2})}$ .

Definition

U(1) ist die Menge der komplexen Zahlen der Form

$e^{i\theta },\theta \in \mathbb {R}$

(also genau der komplexen Zahlen vom Betrag ; man beachte, dass $e^{{i\theta }}$ und $e^{i(\theta +N2\pi )}$ für $N\in \mathbb {Z}$ demselben Element entsprechen)

mit den Gruppenoperationen

$e^{i\theta _{1}}e^{i\theta _{2}}=e^{i(\theta _{1}+\theta _{2})}$

und

$\left(e^{i\theta }\right)^{-1}=e^{-i\theta }.$

Die Gruppe U(1) ist der Spezialfall der unitären Gruppe U(n) für n=1 .

Eigenschaften

ist isomorph zur Drehgruppe und zur Kreisgruppe $S^{1}$ .
ist eine abelsche Gruppe.
ist kompakt.

Darstellungstheorie

Alle Darstellungen über $\mathbb {C}$ sind unitär.
Alle irreduziblen Darstellungen über $\mathbb {C}$ sind 1-dimensional und sind von der Form

$e^{i\theta }\to e^{ik\theta }\in U(1)\subset GL(1,\mathbb {C} )$

für ein $k\in \mathbb {Z}$ .

Es folgt, dass jede -dimensionale Darstellung über $\mathbb {C}$ von der Form

${\mathcal {H}}_{k_{1}}\oplus \ldots \oplus {\mathcal {H}}_{k_{n}}$

mit $\dim({\mathcal {H}}_{k_{1}})=\ldots =\dim({\mathcal {H}}_{k_{n}})=1$ ist, wobei $e^{{i\theta }}$ auf ${\mathcal {H}}_{k_{l}}$ ( $l=1,\ldots ,n$ ) durch Multiplikation mit $e^{ik_{l}\theta }$ wirkt.

Ladungsoperator

Der Ladungsoperator für die Darstellung ${\mathcal {H}}_{q_{1}}\oplus \ldots \oplus {\mathcal {H}}_{q_{n}}$ ist durch die Matrix

$\left({\begin{array}{cccc}q_{1}&0&\ldots &0\\0&q_{2}&\ldots &0\\\ldots &&&\ldots \\0&0&\ldots &q_{n}\end{array}}\right)$

gegeben,

Physik

In der Quantenmechanik werden Teilchen durch komplex-wertige Wellenfunktionen beschrieben und U(1) wirkt auf diesen Wellenfunktionen durch punktweise Phasentransformation $f\to e^{i\theta }f$ des Funktionswerts. Das ist eine globale Eichinvarianz. Als lokale Eichtheorie, in der die Phase $\theta (x,t)$ eine Funktion von Raum und Zeit ist, entspricht die Eichgruppe U(1) der Quantenelektrodynamik (und der klassischen Elektrodynamik). Die Eigenwerte von entsprechen der elektrischen Ladung der Teilchen, wobei für die Phase $Q\theta (x,t)$ angesetzt wurde. In der Quantenelektrodynamik ist der zugrundeliegende Raum der Minkowskiraum und der Formalismus der Relativitätstheorie wird zur Beschreibung benutzt. Das (relativistische) Vektorpotential entspricht hier dem Zusammenhang auf einem U(1)-Prinzipalbündel, der Feldstärketensor der Krümmungs-2-Form des Bündels.

Die Drehungen um eine feste Achse können mit der Gruppe U(1) identifiziert werden. Die Eigenwerte des Ladungsoperators werden als quantisierte Drehimpulse in Richtung der gegebenen Achse interpretiert.

Der eindimensionale harmonische Oszillator hat U(1) -Symmetrie durch Drehungen in der Ort-Impuls-Ebene. In diesem Fall ist ein skalares Vielfaches des Hamilton-Operators.

Im Standardmodell der Elementarteilchenphysik wird die Wechselwirkung der Materiefelder durch abstrakte (mathematische) Eichsymmetrien mit den Eichgruppen U(1) , SU(2) und SU(3) beschrieben. Die letzten beiden Eichgruppen sind nicht-abelsch und die zugehörigen Feldtheorien heißen Yang-Mills-Theorien. Auch in GUTs spielen U(1)-Komponenten als Eichgruppen eine Rolle. Sie tauchen nicht unbedingt in der vollen Eichgruppe auf, sondern wenn diese durch spontanen Symmetriebruch zerfällt. Es gibt aber auch subtilere Anwendungen einer U(1)-Symmetrie (global und lokal) in der Elementarteilchentheorie.

Ein Beispiel der Anwendung in der Festkörperphysik ist der ganzzahlige Quanten-Hall-Effekt, dessen ganzzahlige Quantenzahlen der elektrischen Leitfähigkeit durch eine topologische Invariante gegeben sind, die der ersten Chernklasse eines U(1)-Faserbündels entspricht (für die Identifizierung solcher und anderer topologischer Phasen in der Festkörperphysik erhielt David J. Thouless 2016 den Nobelpreis für Physik).

Basierend auf einem Artikel in:

Wikipedia.de