Grothendieck-Gruppe
Die Grothendieck-Gruppe ist eine mathematische Konstruktion, die einer kommutativen Halbgruppe eine Gruppe zuordnet. Diese nach Alexander Grothendieck benannte Konstruktion ist der Lokalisierung aus der Ringtheorie nachempfunden und kann wie diese durch eine universelle Eigenschaft beschrieben werden.
Universelle Eigenschaft
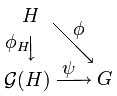
Es gilt folgender Satz:
Ist
eine kommutative Halbgruppe, so gibt es eine kommutative Gruppe
und einen Halbgruppen-Homomorphismus
mit folgender Eigenschaft: Zu jeder Gruppe
und jedem Halbgruppen-Homomorphismus
gibt es genau einen Gruppen-Homomorphismus
mit
.
Konstruktion
Ein Beweis ergibt sich aus folgender Konstruktion, die der Lokalisierung aus
der Ringtheorie nachempfunden ist. Sei
eine kommutative Halbgruppe. Auf dem kartesischen
Produkt
definiere man eine Äquivalenzrelation
durch
.
Man zeigt nun, dass dies tatsächlich eine Äquivalenzrelation definiert, die
Äquivalenzklasse
von
wird mit
bezeichnet. Man setzt nun
und zeigt weiter, dass durch
eine Gruppenverknüpfung auf
definiert wird. Dabei ist
das neutrale Element (unabhängig von
),
die Inversenbildung ist durch die Formel
gegeben. Setzt man schließlich
,
so kann man zeigen, dass
und
die Bedingung aus der universellen Eigenschaft erfüllen.
Eigenschaften
- Wie üblich zeigt man mit Hilfe der universellen Eigenschaft, dass die
Gruppe
bis auf Isomorphie eindeutig bestimmt ist. Man nennt daher
die Grothendieck-Gruppe von
.
- Der Halbgruppen-Homomorphismus
aus obiger universeller Eigenschaft ist genau dann injektiv, wenn die Halbgruppe die Kürzbarkeitseigenschaft hat.
Beispiele
- Für die Halbgruppe
fällt die Bildung der Grothendieck-Gruppe mit der üblichen Konstruktion der ganzen Zahlen zusammen. Man hat daher
, wobei der Isomorphismus durch
gegeben ist. Identifiziert man die Grothendieck-Gruppe von
mit
, so ist
die Inklusion
. Dabei spielt es keine Rolle, ob man unter
die natürlichen Zahlen mit oder ohne Null versteht.
- Ganz ähnliche Überlegungen zur multiplikativen Halbgruppe
führen zu
, und bei dieser Identifikation fällt
wieder mit der Inklusion
zusammen.
- Bei der multiplikativen Halbgruppe
(der Index 0 signalisiere, dass die Null zu
gehört) liegt keine Kürzungseigenschaft vor. In diesem Fall sind je zwei Paare
und
äquivalent, denn es gilt
. Daher ist
und
für alle
.
Grothendieck-Gruppe als Funktor
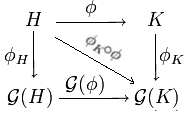
Die oben beschriebene Konstruktion ordnet jeder kommutativen Halbgruppe eine
kommutative Gruppe zu. Ist
ein Halbgruppen-Homomorphismus in der Kategorie
der kommutativen Halbgruppen, so kann man wie folgt einen Gruppenhomomorphismus
konstruieren. Mittels
erhält man zunächst einen Halbgruppen-Homomorphismus
und daraus mittels der universellen Eigenschaft einen Gruppen-Homomorphismus
mit
.
Durch diese Definition wird
zu einem kovarianten
Funktor von der Kategorie
in die Kategorie
der abelschen Gruppen.
Betrachtet man eine abelsche Gruppe
nur als Halbgruppe, so kann man
bilden. Es stellt sich heraus, dass
,
wobei der Isomorphismus durch
gegeben ist. In der Tat ist
linksadjungiert
zum Vergissfunktor
.
Anwendung
Neben der oben beschriebenen Konstruktion der ganzen Zahlen aus den
natürlichen Zahlen ist die Bildung der K0-Gruppe eines Ringes eine wichtige
Anwendung. Zu jedem Ring
betrachtet man die Menge
(!)
der Isomorphieklassen endlich
erzeugter
projektiver
-links-Moduln
mit der direkten
Summe als Halbgruppenverknüpfung. Die K0-Gruppe des Ringes
wird dann als Grothendieck-Gruppe von
definiert.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.06. 2021