Treppenfunktion (reelle Funktion)

Beispiel einer Treppenfunktion

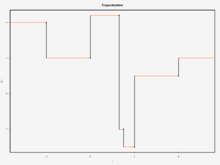
Eine Treppenfunktion ist in der Mathematik eine spezielle reelle Funktion, die nur endlich viele Funktionswerte annimmt und stückweise konstant ist. Dadurch erhält der Funktionsgraph einer Treppenfunktion sein charakteristisches und namensgebendes Aussehen, das einer auf- und absteigenden Treppe ähnelt.

Definition

Eine Funktion

$f\colon [a;b]\to \mathbb {R}$

heißt eine Treppenfunktion, wenn es Zahlen $t_{0},t_{1},\dotsc ,t_{n}$ mit

$a=t_{0}<t_{1}<t_{2}<\dotsb <t_{n}=b$

gibt und Zahlen $c_{1},c_{2},\dotsc ,c_{n}$ , sodass

$f(x)=c_{i}{\text{ für alle }}x\in (t_{i-1},t_{i})$

und alle $i=1, \dotsc, n$ gilt. Dabei sind die Funktionswerte $f(t_{i})$ an den „Stützstellen“ beliebig, aber reell.

Verwendung

Treppenfunktionen benutzt man auch zur Approximation von Integralen. Das Integral einer Treppenfunktion wird durch

$\int _{a}^{b}f(x)\,\mathrm {d} x=\sum _{i=1}^{n}c_{i}\ell (I_{i})$

definiert. Der Vorteil ist hier, dass man ohne Grenzwertprozess auskommt und nur endliche Summen hat. In der Summenformel bezeichnet $c_{i}$ den Wert von auf dem Intervall $I_{i}=(t_{i-1},t_{i})$ sowie $\ell (I_{i})$ die Länge dieses Intervalls, also $t_{i}-t_{t-i}$ .

Bereits durch die einfache Definition des Integrals einer Treppenfunktion hat man ein starkes mathematisches Hilfsmittel gewonnen: Jede beschränkte, stetige Funktion $f\colon D\rightarrow Y$ mit $D,Y\subseteq \mathbb {R}$ kann beliebig genau durch eine Treppenfunktion approximiert werden. Also kann auch das Integral dieser Funktion beliebig genau approximiert werden. Diese Tatsache ist ein wichtiges Fundament für die Definition des Riemann-Integrals. Auf diese Weise hat Jean Gaston Darboux die Einführung des Riemann-Integrals vereinfacht.

Beispiele

Die Heaviside-Funktion ist 0 für jede negative Zahl, sonst 1.
Rechteckfunktion
Abrundungsfunktion und Aufrundungsfunktion

Abgrenzung

Die Treppenfunktionen sind sowohl den einfachen Funktionen als auch den Sprungfunktionen sehr ähnlich, sollten aber nicht mit diesen verwechselt werden.

So nehmen beispielsweise einfache Funktionen auch nur endlich viele Werte an, können aber trotzdem viel komplexer sein, da sie nicht über Intervalle auf dem Grundraum definiert werden, sondern über messbare Mengen. So ist beispielsweise die Dirichlet-Funktion eine einfache Funktion, aber keine Treppenfunktion im hier genannten Sinne, da sie überabzählbar viele Sprungstellen hat und in keinem noch so kleinen Intervall konstant ist. Außerdem werden einfache Funktionen auf beliebigen Messräumen definiert, wohingegen Treppenfunktionen bloß auf $\mathbb {R}$ definiert werden. Allerdings ist jede Treppenfunktion auch immer eine einfache Funktion.

Die Sprungfunktionen sind wie die Treppenfunktionen auch auf den reellen Zahlen definiert. Allerdings sind sie immer monoton wachsend, können aber auch abzählbar viele Sprungstellen haben.

Verallgemeinerung

Eine stochastische Verallgemeinerung einer Treppenfunktion ist ein elementarer vorhersagbarer stochastischer Prozess. Er spielt für die Konstruktion des Ito-Integrals eine ähnliche Rolle wie die einfachen Funktionen für die Konstruktion des Lebesgue-Integrals.

Basierend auf einem Artikel in:

Wikipedia.de