Molekülschwingung
Als Molekülschwingung wird eine periodische Bewegung von benachbarten Atomen in einem Molekül verstanden. Diese Schwingungen treten in jedem Molekül auf. Sie können über die Zufuhr von Energie angeregt werden, beispielsweise durch die Absorption von elektromagnetischer Strahlung. Die Absorption und die Emission der Strahlung bildet die Grundlage für die Verfahren der Schwingungsspektroskopie, wie die Infrarot- oder die Raman-Spektroskopie. Die Frequenz der periodischen Bewegung wird als Schwingungsfrequenz bezeichnet.
Normalschwingungen
Der einfachste Fall eines Moleküls ist das zweiatomige Molekül, beispielsweise molekularer Sauerstoff (O2) und Stickstoff (N2) oder Kohlenstoffmonoxid (CO). Diese Moleküle haben nur einen Schwingungsfreiheitsgrad entlang der Bindungsachse, weil die zwei Atome nur bezüglich ihres einen Abstandes schwingen können. Es handelt sich hierbei also um eine Streckschwingung oder Valenzschwingung. Bei mehratomigen Molekülen ergibt sich durch weitere voneinander unabhängige Schwingungsarten ein komplizierteres Schwingungsverhalten, die sogenannten Normalschwingungen.
Die Anzahl der möglichen Normalschwingungen ergibt sich aus den
Bewegungsmöglichkeiten der Atome im Raum. Dabei hat jedes einzelne Atom drei
Bewegungsfreiheitsgrade,
die den drei Raumachsen entsprechen. Demzufolge besitzen
Atome
Freiheitsgrade. In einem aus
Atomen bestehenden Molekül ist zwar jedes Atom mit mindestens einem anderen Atom
„verbunden“, d.h., es kann sich nicht beliebig in jeder Richtung bewegen.
Da ein Molekül aber nicht vollkommen starr ist, können sich die Atome aber doch
in allen Richtungen ein wenig gegeneinander bewegen, sodass sich die Anzahl der
Freiheitsgrade im Molekül nicht unter
Freiheitsgrade können nun so aufgeteilt werden:
- Drei Freiheitsgrade entfallen auf Translationen des gesamten Moleküls in x-, y- und z-Richtung;
- zwei (bei linearen Molekülen, wo die Rotation um die Achse nicht beobachtet werden kann) oder drei (bei gewinkelten Molekülen) entfallen auf Molekülrotationen im Raum.
Für die Schwingungsfreiheitsgrade (auch als Schwingungsmoden,
Normalschwingung oder Eigenschwingung bezeichnet) bleiben daher
bzw.
Freiheitsgrade übrig.
So weist beispielsweise das lineare 3-atomige Kohlenstoffdioxid-Molekül
(CO2)
Normalschwingungen auf, die man als asymmetrische und symmetrische
Valenzschwingung (νas und νs) sowie als
Deformationsschwingungen (δ) parallel und senkrecht zur Zeichenebene bezeichnet.
Das geknickte Wassermolekül (H2O) hat hingegen
Schwingungsmoden.
Schwingungsformen
Für zwei- und dreiatomige Moleküle ergeben sich nur wenige Normalschwingungen (höchstens 5), die sich in zwei Gruppen einordnen lassen und oft in den sogenannten meckeschen Symbolik bezeichnet werden:
- Valenzschwingungen (Streckschwingungen): Schwingungen entlang der Bindungsachse zweier Atome in einem Molekül durch eine Dehnung oder Stauchung der Bindung
- Deformationsschwingungen:
Schwingungen unter der Deformation des Bindungswinkels
- in der Ebene (Biege-/Beugeschwingungen)
- außerhalb der Ebene (Dreh-/Kippschwingungen) – meist senkrecht zur Bindungsebene
Diese Schwingungen lassen sich auch an Molekülgruppen aus 3 oder 4 Atomen bestimmen, beispielsweise den für organische Verbindungen typischen Methylen- (> CH2) oder Methylgruppen (–CH3).
- Streckschwingungen am Beispiel der Methylengruppe
-
 Symmetrische Streckschwingung
Symmetrische Streckschwingung
(engl. symmetrical stretching) -
 Antisymmetrische Streckschwingung
Antisymmetrische Streckschwingung
(engl. antisymmetrical stretching)
- Deformationsschwingungen am Beispiel der Methylengruppe
-
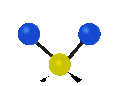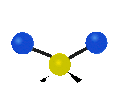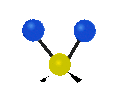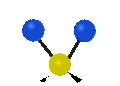
 „Schaukelschwingung“
„Schaukelschwingung“
(engl. rocking) -
 Scher-/Deformations-
Scher-/Deformations-
schwingung
(engl. scissoring oder bending) -
 Drehschwingung
Drehschwingung
(engl. twisting oder torsing) -
 „Wippschwingung“
„Wippschwingung“
(engl. wagging)
Beispiel: Ethen
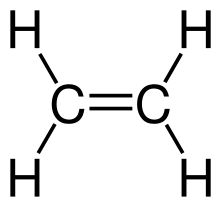
In diesem Abschnitt sollen noch einmal am Beispiel der organischen Verbindung
Ethen die
auftretenden Normalschwingungen dargestellt werden. Ethen besteht aus 6 Atomen
und besitzt eine planare, gewinkelte Struktur. Daher ergeben sich insgesamt
Normalschwingungen, die wie folgt zugeordnet werden können:
- 5 Valenzschwingungen aufgrund der Längenänderung der C–H- (4×) oder C=C-Bindungen (1×)
- 2 Scherschwingungen der beiden H–C–H-Gruppen, durch die Änderung des Winkels in der Methylengruppe
- 2 Schaukelschwingungen durch die Änderung des Winkels zwischen einer Gruppe von Atomen, beispielsweise der Methylen-Gruppe und dem Rest des Moleküls.
- 2 Wippschwingung durch die Änderung des Winkels zwischen der Ebene, in der eine Gruppe von Atomen, beispielsweise der Methylen-Gruppe, liegt und der Ebene, welche von den übrigen Konstituenten aufgespannt wird.
- 1 Drehschwingung durch die Änderung des Winkels in den beiden Methylengruppen.
Man beachte, dass die H–C=C-Winkel nicht als innere Koordinaten verwendbar sind, da die Winkel an jedem Kohlenstoffatom nicht alle gleichzeitig erhöht werden können.
Nichtstarre Moleküle
Neben den Normalschwingungen, bei denen entweder die Bindungslänge oder der Bindungswinkel verändert wird, können innermolekulare Schwingungen auftreten, bei denen die Konfiguration des Moleküls geändert wird. Ein solches Molekül bezeichnet man als nichtstarr (engl. non rigid). Beispielsweise können beim Ammoniak-Molekül die drei Wasserstoffatome um das Stickstoffatom hinweg schwingen, sodass es zu einer Inversion kommt. Die dazu benötigte Energie beträgt etwa 24,3 kJ/mol. Diese Konfigurationsänderungen können bei Molekülen mit mindestens drei beweglichen Bindungen auftreten. Bei Molekülen mit vier Bindungen (Tetraederkonfiguration), wie Methan, kann es in der Regel zu keiner Inversion kommen. Ein solches Molekül ist starr. Bei fünf beweglichen Bindungen ist dagegen wieder eine Inversion möglich. Das Phosphorpentafluorid-Molekül kann aus einer trigonalen Bipyramide in eine quadratische Pyramide überführt werden. Die Energiebarriere hierfür beträgt etwa 25 kJ/mol. Oktaedrische Moleküle mit sechs Bindungen sind dagegen wieder besonders starr.
Anregung durch elektromagnetische Strahlung
Eine molekulare Schwingung wird angeregt, wenn das Molekül ein Quant mit der
Energie
absorbiert. Hierbei ist
die Frequenz der Schwingung und
das plancksche Wirkungsquantum. Das Molekül wird auf seine Normalschwingung
angeregt, wenn ein solches Quant durch das Molekül im Grundzustand absorbiert
wird. Wenn ein weiteres Quant absorbiert wird, wird der erste „Oberton“
angeregt. Weitere absorbierte Quanten regen das Molekül zu höheren „Obertönen“
an.
In erster Näherung kann die Bewegung einer Normalschwingung als eine Art einfache harmonische Bewegung beschrieben werden. In dieser Näherung ist die Schwingungsenergie eine quadratische Funktion (Parabel) in Bezug auf die räumliche Verschiebungen der Atome und der erste „Oberton“ (höhere Schwingungsmode) hat die doppelte Frequenz des „Grundtons“. In Wirklichkeit sind Schwingungen anharmonisch und der erste „Oberton“ hat eine Frequenz, die etwas niedriger ist als das Doppelte des Grundtons. Die Anregung der höheren „Obertöne“ beinhaltet immer weniger zusätzliche Energie und führt schließlich zur Dissoziation des Moleküls, da die potentielle Energie des Moleküls mit größerem Abstand immer flacher ausläuft.
Die Schwingungszustände eines Moleküls können durch eine Vielzahl von Methoden untersucht werden. Der direkteste Weg ist die Untersuchung mithilfe der Infrarotspektroskopie, denn die zur Anregung von Schwingungen notwendige Energie entspricht bei den meisten Verbindungen der Energie eines Photons im Infrarotbereich. Eine weitere häufig angewendete Methode, um die Schwingungen direkt zu messen, ist die Raman-Spektroskopie, bei der üblicherweise sichtbares Licht verwendet wird.
Die Schwingungsanregung kann aber auch durch elektronische Anregung (vibronischer Übergang) erfolgen. Auf diesem Weg kann die Schwingungsfeinstruktur untersucht werden. Dies gilt vor allem für Moleküle im Gaszustand.
Bei gleichzeitiger Anregung einer Molekülschwingung und -rotation entstehen Rotations-Schwingungs-Spektren.
Normalkoordinaten
Die Normalkoordinaten beziehen sich auf die Normalmoden der Schwingungen der Atome aus ihren Gleichgewichtslagen heraus. Jede Normalmode ist einer einzigen Normalkoordinate zugewiesen. Formal sind Normalschwingungen durch Diagonalisierung einer Matrix bestimmt (siehe Eigenmode), so dass jede Normalmode eine unabhängige Molekülschwingung ist, die mit einem eigenen Spektrum von quantenmechanischen Zuständen verbunden ist. Wenn das Molekül Symmetrien besitzt, gehört es zu einer Punktgruppe, und die Normalmoden entsprechen einer irreduziblen Darstellung der Punktgruppe. Die Normalschwingung kann dann qualitativ durch die Anwendung der Gruppentheorie und Projektion der irreduziblen Darstellung auf die Darstellung in kartesischen Koordinaten bestimmt werden. Ein Beispiel hierfür ist die Anwendung auf das CO2-Molekül. Dabei stellt man fest, dass die C=O-Streckschwingungen sich in eine symmetrische und ein asymmetrische O=C=O-Streckschwingung zerlegen lassen:
- symmetrische Streckschwingung: die Summe der beiden C–O-Streckkoordinaten. Dabei ändert sich die Länge der beiden C–O-Bindungen um den gleichen Betrag und das Kohlenstoffatom ist feststehend: Q = q1 + q2
- asymmetrische Streckschwingung: die Differenz der beiden C–O-Streckkoordinaten. Dabei nimmt die Länge der einen C–O-Bindung zu, während die andere abnimmt: Q = q1 − q2
Wenn zwei oder mehr Normalkoordinaten die gleiche nicht weiter reduzierbare Darstellung der molekularen Punktgruppe haben (umgangssprachlich, sie haben die gleiche Symmetrie), dann gibt es eine "Mischung" und die beiden Koeffizienten der Kombination können nicht mehr a priori bestimmt werden. Ein Beispiel dafür sind die beiden Streckschwingungen im linearen Molekül Cyanwasserstoff (HCN)
- hauptsächlich eine C–H-Streckschwingung mit einer kleinen C–N-Streckschwingung; Q1 = q1 + a q2 (a ≪ 1)
- hauptsächlich eine C–N-Streckschwingung mit einer kleinen C–H-Streckschwingung; Q2 = b q1 + q2 (b ≪ 1)
Die Koeffizienten a und b sind durch eine vollständige Analyse der Normalkoordinaten mittels der GF-Methode von Edgar Bright Wilson gefunden worden.
Newtonsche Mechanik
-
 Molekül zwischen zwei ungeladenen Kondensatorplatten
Molekül zwischen zwei ungeladenen Kondensatorplatten -
 Molekül richtet sich im elektromagnetischen Feld aus und vergrößert seinen Bindungsabstand
Molekül richtet sich im elektromagnetischen Feld aus und vergrößert seinen Bindungsabstand
Ein einfaches Modell für die Erklärung der Anregung von Molekülschwingungen und auch -rotationen ist das Verhalten eines permanenten elektrischen Dipols in einem elektrischen Feld gemäß der klassischen newtonschen Mechanik. Dabei wirken durch das äußere Feld Kräfte auf den Dipol. Für das im nebenstehenden Bild dargestellte Modell einer Dipolanregung durch das (statische) elektrische Feld eines Plattenkondensator ergeben sich daher folgende Reaktionen.
- Der Dipol bzw. das Molekül richtet sich entlang des elektrischen Feldes aus
- Durch die wirkenden Kräfte vergrößert sich der Bindungsabstand.
Wird jetzt Wechselspannung angelegt oder regt man das Molekül mit einer elektromagnetischen Welle an, fangen die an den Bindungen „hängenden“ funktionellen Gruppen zu schwingen und zu rotieren an.
Grundlage ist dabei, dass zwischen gebundenen Atomen in einem Molekül
anziehende und abstoßende Kräfte wirken. Der optimale Bindungsabstand im Molekül
befindet sich in einem Minimum der zugehörigen Potentialfunktion. Vereinfacht
gesehen, kann die Bindung zwischen den Atomen als eine Art Feder und die
Molekülschwingung daher als Federschwinger betrachtet werden. Unter der Annahme
einer harmonischen Näherung gehorcht – der anharmonische Oszillator wird unter
anderem in Califano (1976)
betrachtet – die Feder dem hookschen
Gesetz, das heißt, die erforderliche Kraft
ist zur Längenänderung der Feder proportional. Die Proportionalitätskonstante
k wird als Kraftkonstante bezeichnet.
Gemäß dem zweiten newtonschen Gesetz ist diese Kraft gleich dem Produkt aus der reduzierten Masse μ und der Beschleunigung.
Da es sich um ein und dieselbe Kraft handelt, ergibt sich die gewöhnliche Differentialgleichung:
Die Lösung dieser Gleichung für eine einfache harmonische Bewegung ist:
wobei A die maximale Amplitude der Schwingungskomponente Q ist. Es bleibt, die reduzierte Masse μ zu definieren. Im Allgemeinen ist die reduzierte Masse eines zweiatomigen Moleküls AB mit den jeweiligen Atomgewichten mA und mB:
Die Verwendung der reduzierten Masse stellt sicher, dass das Massenzentrum des Moleküls nicht durch die Schwingung beeinträchtigt wird. Im Fall der harmonischen Näherung ist die potentielle Energie des Moleküls eine quadratische Funktion der jeweiligen Normalkoordinaten. Daraus folgt, dass die Kraftkonstante gleich der zweiten Ableitung der potentiellen Energie ist:
Wenn zwei oder mehr Normalschwingungen die gleiche Symmetrie haben, muss eine vollständige Normalkoordinatenanalyse durchgeführt werden (GF-Methode). Die Schwingungsfrequenzen νi können aus den Eigenwerten λi des Matrizenprodukts GF bestimmt werden. G ist eine Matrix von Zahlen, die aus den Massen der Atome und der Geometrie des Moleküls bestimmt wurde. F ist eine Matrix, die aus den Werten der Kraftkonstanten bestimmt wird. Details über die Bestimmung der Eigenwerte können unter anderem in Gans (1971) gefunden werden.
Dieses mechanistische Modell ist allerdings nur begrenzt anwendbar, denn erstens kann es keine Moleküle ohne ein permanentes Dipolmoment beschreiben und zweitens kann es nicht erklären, warum nur diskrete Energien für die Anregung zugelassen sind.
Quantenmechanische Beschreibung
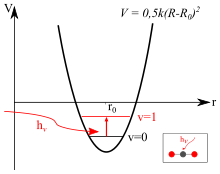
Wie auch im Modell der klassischen Mechanik ist die Grundlage des
quantenmechanischen Modells der Schwingungs- und Rotationsanregung die
Potentialfunktion. Die Potentialfunktion lässt sich für den Fall der
harmonischen Näherung in ihrem Minimum gut durch eine quadratische Funktion
nähern (eine solche Parabel ergibt sich aus der Integration des hookeschen
Federgesetzes.) Durch Anregung der Schwingung, beispielsweise durch die
Absorption von elektromagnetischer Strahlung, fängt das Molekül an zu schwingen
und die Schwingung wird aus dem Grundzustand in den ersten angeregten
Schwingungszustand angehoben. Für die Bestimmung der dazu notwendigen Energie
muss die Schrödinger-Gleichung
für dieses Potential gelöst werden. Nach Abtrennung der Relativbewegung von
Atomkernen und Elektronen (Born-Oppenheimer-Näherung)
ergibt sich als Lösung der Schrödinger-Gleichung ein Zusammenhang zwischen der
benötigten Energie, der Bindungsstärke ()
und der reduzierten
Masse (
).
Anders als beim klassischen harmonischen Oszillator ist im quantenmechanischen
Fall die Schwingungsenergie durch die Schwingungsquantenzahl
gequantelt:
mit
dem reduzierten
Planckschen Wirkungsquantum und dem Potential
(siehe Harmonischer
Oszillator). Die Lösung der Schrödinger-Gleichung ergibt folgende
Energiezustände:
Unter Kenntnis der Wellenfunktionen können bestimmte Auswahlregeln formuliert werden. Zum Beispiel sind für einen harmonischen Oszillator nur Übergänge erlaubt, wenn sich die Quantenzahl n nur um 1 ändert:
,
aber diese gelten nicht für einen anharmonischen Oszillator; die Beobachtung
von „Obertönen“ ist nur möglich, weil Schwingungen anharmonisch sind. Eine
weitere Folge dieses anharmonischen Charakters ist, dass die Übergänge zwischen
den Zuständen
und
etwas weniger Energie haben als Übergänge zwischen dem Grundzustand und ersten
angeregten Zustand. Ein solcher Übergang führt zu einem „heißen Übergang“ (engl.
hot transition) bzw. einer „heißen Bande“ (engl. hot band).
Literatur
- Salvatore Califano: Vibrational States. John Wiley & Sons, New York 1976.
- P. Gans: Vibrating molecules. An introduction to the interpretation of infrared and Raman spectra. Chapman and Hall, 1971.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.06. 2024