Ratengleichung

Ratengleichungen sind Gleichungen, welche bei gekoppelten chemischen Reaktionen den zeitlichen Konzentrationsverlauf verschiedener chemischer Stoffe beschreiben, oder bei An- und Abregungsprozessen den Besetzungsverlauf der Energieniveaus in Atomen oder Molekülen.

Ratengleichungen beschreiben die Reaktionskinetik.

Die Änderungsrate der Konzentration $c_{i}$ einer Spezies ist die Summe der Änderungsraten der Konzentrationen, welche durch verschiedene Reaktionen hervorgerufen werden:

${\frac {\mathrm {d} c_{i}}{\mathrm {d} t}}=\sum _{j=1}^{N_{\mathrm {R} }}{\frac {\mathrm {d} c_{i,r}}{\mathrm {d} t}}=\sum _{j=1}^{N_{\mathrm {R} }}\nu _{i,j}r_{j},$ ,

wobei die betrachtete Spezies ist, $c_{i}$ ihre Konzentration und ein Index ist, der über alle auftretenden Reaktionen (also auch jeweils über die Hin- und Rückreaktion) läuft. $r_{j}$ ist die Reaktionsgeschwindigkeit der Reaktion . Die Reaktionsgeschwindigkeit $r_{j}$ ist proportional zum Produkt der Eduktaktivitäten $a_{j,l}^{|\nu _{j,l}|}$ der Reaktion , mit der Geschwindigkeitskonstante k_j der Reaktion als Proportionalitätskonstante:

$r_{j}=k_{j}\prod _{l}a_{j,l}^{|\nu _{j,l}|}$ .

Dadurch ergibt sich die die Ratengleichung als:

${\frac {\mathrm {d} c_{i}}{\mathrm {d} t}}=\sum _{j=1}^{N_{\mathrm {R} }}\nu _{ij}k_{j}\prod _{k=1}^{N_{j}}a_{k}^{b_{kj}},$

wobei

$a_{i}$ die Aktivität der Spezies $i\,$ – häufig wird vereinfachend die Konzentration $c_{i}$ verwendet –,
$\nu_{ij}$ die stöchiometrischen Koeffizienten der Spezies in der Reaktion ,
$b_{{ij}}$ die Beträge der stöchiometrischen Koeffizienten, falls die Ratengleichung mit Aktivitäten aufgestellt ist, oder die partiellen Reaktionsordnungen der Spezies in der Reaktion (im Allgemeinen ungleich den stöchiometrischen Koeffizienten), falls die Ratengleichung mit Konzentrationen aufgestellt ist,
die Ratenkoeffizienten (i.A. Geschwindigkeitskonstanten),
$N_{\mathrm {R} }$ die Anzahl der Reaktionen und
die Anzahl der beteiligten Stoffe in der Reaktion ist.

Bei den Ratengleichungen handelt es sich im Allgemeinen um ein System von gekoppelten, steifen, nichtlinearen Differentialgleichungen erster Ordnung, für die die Bausteinerhaltung gelten muss. Im stationären Fall $(\mathrm {d} c_{i}/\mathrm {d} t=0)$ ergibt sich das Massenwirkungsgesetz. Ratengleichungen können kompakt mithilfe der Stöchiometrischen Matrix dargestellt werden.

Durch Lösung der Differentialgleichungen erhält man den zeitlichen Verlauf der mittleren Konzentrationen. Um Realisierungen der Konzentrationen inklusive Fluktuationen zu erhalten, können stochastische Simulationen mit dem Gillespie-Algorithmus ausgeführt werden.

Herleitung

Die Ratengleichungen lassen sich für alle beteiligten Spezies herleiten, indem die Kontinuitätsgleichung mit Quell- beziehungsweise Senkterm (bzw. eine Bilanzgleichung) für die Teilchenkonzentrationen aufgestellt werden:

${\frac {\partial c_{i}}{\partial t}}+\operatorname {div} {\vec {j}}_{i}=f_{i}(\{a_{i}\})$ ,

wobei $f_{i}(\{a_{i}\})$ der Quellterm ist, welcher von den Aktivitäten $a_{i}(\{c_{i}\})$ abhängt. Diese Aktivitäten sind im Allgemeinen wiederum nichttrivial von allen Konzentrationen abhängig.

Da eine Gleichgewichtsreaktion immer eine Hinreaktion und eine Rückreaktion besitzt, existieren die Hin-Reaktionsrate $k_{\text{+,r}}$ und die Rück-Reaktionsrate $k_{\text{-,r}}$ . Der Quellterm ist durch eine Summe über alle Reaktionen gegeben:

$f_{i}(\{a_{i}\})=\sum _{r}|\nu _{i,r}|\left[-k_{\text{-,r}}\prod _{{\text{Reaktanden j}},r}a_{r,j}^{|\nu _{r,j}|}+k_{\text{+,r}}\prod _{{\text{Produkte j}},r}a_{r,j}^{|\nu _{r,j}|}\right].$

Man beachte, dass die partielle Reaktionsordnung (der Exponent, mit dem die Konzentrationen eingehen) nur dann dem Betrag der stöchiometrischen Koeffizienten entspricht, wenn Aktivitäten verwendet werden. Werden statt Aktivitäten ebenfalls Konzentrationen im Quellterm verwendet und liegen Teilchenwechselwirkungen vor, so sind die Beträge der stöchiometrischen Koeffizienten mit den partiellen Reaktionsordnungen zu ersetzen. Die partielle Reaktionsordnung kann beliebige Werte annehmen (z.B. 0) und wird experimentell bestimmt.

Verschiedene Fälle

Im Gleichgewicht gibt es keine Teilchenströme ( ${\vec {j}}_{i}={\vec {0}}\,\forall i$ ) und die Teilchenkonzentrationen ändern sich nicht mehr zeitlich. Daher gilt im Gleichgewicht:

$0=f_{i}(\{a_{i}\}).$

Unter der Annahme, dass jede Reaktion (als Paar von Hin- und Rückreaktion) im Einzelnen ausgeglichen ist, erhält man für jede Reaktion das Massenwirkungsgesetz durch Umformung:

$K_{r}={\frac {k_{\text{-,r}}}{k_{\text{+,r}}}}={\frac {\prod _{{\text{Produkte j}},r}a_{r,j}^{|\nu _{r,j}|}}{\prod _{{\text{Reaktanden j}},r}a_{r,j}^{|\nu _{r,j}|}}}$

Ist das System im Nichtgleichgewicht, aber homogen, so treten keine Teilchenströme auf, jedoch ändern sich die Konzentrationen zeitlich, bis das Gleichgewicht erreicht ist:

${\frac {\partial c_{i}}{\partial t}}=f_{i}(\{a_{i}\})$

Für den Fall, dass man ein inhomogenes System im Nichtgleichgewicht betrachtet, ist der Teilchenstrom ${\vec {j}}_{i}\neq 0$ und kann durch das erste Fick’sche Gesetz

${\vec {j}}_{i}=-{\vec {\nabla }}(D_{i}c_{i}({\vec {r}}))+{\vec {j}}_{i}^{\text{excess}}$

beschrieben werden (wobei der nicht-ideale Exzess-Term nur für nicht-ideale Systeme auftritt). Man erhält dann eine Reaktionsdiffusionsgleichung.

Für den Fall, dass es zusätzlich Strömung im System gibt, ist Konvektion im Teilchenstrom zu berücksichtigen und man erhält die Konvektions-Diffusions-Gleichung.

Ratenkoeffizenten

→ Hauptartikel: Geschwindigkeitskonstante

Die in den Ratengleichungen auftretenden Reaktionsratenkoeffizienten können allgemein als beliebige Funktionen der jeweiligen, gegebenenfalls zeitabhängigen Temperatur (siehe auch Plasmaphysik: Thermisches Gleichgewicht) betrachtet werden. Im Allgemeinen müssen Ratenkoeffizienten für chemische Prozesse der schweren Teilchen aus der Literatur entnommen werden ('Geschwindigkeitskonstante' einer chemischen Reaktion), die Ratenkoeffizienten für die elektronenstoßinduzierten Prozesse können mit Hilfe der Elektronenkinetik erhalten werden.

Grundlage für die kinetische Behandlung der Elektronen, sowohl zur Berechnung derartiger Ratenkoeffizienten, als auch elektronischer Transportprozesse (elektrische Leitfähigkeit) bildet die Boltzmann-Gleichung für die Elektronenenergieverteilung.

Beispiele

Wasserstoffoxidation

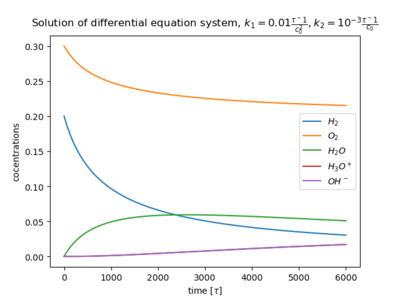
Numerische Lösung. Die Reaktionsraten $k_{1},k_{2}$ und die Anfangskonzentrationen sind in diesem Beispiel beliebig gewählt. $c_{0}$ ist eine Referenzkonzentration.

Zur Verdeutlichung wird die Wasserstoffoxidation herangezogen:

$\displaystyle \mathrm {2H_{2}+O_{2}\longrightarrow 2H_{2}O}$

(Ratenkoeffizient: $\displaystyle k_{1}$ )

ein Teil dissoziiert

$\displaystyle \mathrm {2H_{2}O\longrightarrow H_{3}O^{+}+OH^{-}}$

(Ratenkoeffizient: $\displaystyle k_{2}$ )

Die Ratengleichungen (Gl.1) für die fünf Spezies lauten:

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[H_{2}]} =-2k_{1}\mathrm {[H_{2}]^{2}[O_{2}]}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[O_{2}]} =-k_{1}\mathrm {[H_{2}]^{2}[O_{2}]}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[H_{2}O]} =+2k_{1}\mathrm {[H_{2}]^{2}[O_{2}]} -2k_{2}\mathrm {[H_{2}O]^{2}}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[H_{3}O^{+}]} =+k_{2}\mathrm {[H_{2}O]^{2}}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[OH^{-}]} =+k_{2}\mathrm {[H_{2}O]^{2}}$

Die Konzentrationen der Spezies:

$c_{1}\equiv \mathrm {[H_{2}]} ,\;\;c_{2}\equiv \mathrm {[O_{2}]} ,\;\;c_{3}\equiv \mathrm {[H_{2}O]} ,\;\;c_{4}\equiv \mathrm {[H_{3}O^{+}]} ,\;\;c_{5}\equiv \mathrm {[OH^{-}]}$

Belousov-Zhabotinsky-Reaktion

Oszillierende Reaktionen werden durch Ratengleichungen beschrieben. Für spezielle Modelle hierzu, Oregonator und Brüsselator. Die numerische Lösung solcher Differentialgleichungssysteme liefert dann oszillierende chemische Konzentrationen.

Lotka-Volterra-Gleichungen

Die Wechselwirkung von Räuber- und Beutepopulationen wird durch die Lotka-Volterra-Gleichungen beschrieben.

Numerische Lösungsmethoden

Da es sich bei den Ratengleichungen um ein System von steifen Differentialgleichungen handelt, ist man gezwungen ein Verfahren mit einem möglichst großen Stabilitätsgebiet zu wählen, damit die Integrationsschritte nicht allzu klein werden. Am günstigsten sind A-stabile Verfahren.

Für die Ratengleichungen bedeutet 'steif', dass sich die Zeitkonstanten der verschiedenen Spezies sehr stark unterscheiden: Im Verhältnis zu anderen ändern sich einige Konzentrationen nur sehr langsam. Zwei Beispiele absolut steif-stabiler Integrationsverfahren sind die Implizite Trapez-Methode und die Implizite Euler-Methode, ebenso sind einige BDF-Verfahren (backward differentiation formula) geeignet.

Bausteinerhaltung

Das Prinzip der Bausteinerhaltung liefert eine Möglichkeit, die Güte der numerischen Lösungen zu überprüfen, denn es gilt zu jedem Zeitpunkt:

$\sum _{i=1}^{N_{\mathrm {Sp} }}c_{i}\beta _{ik}=\gamma _{k}={\text{const.}},\quad \forall k=1,\dots ,N_{\mathrm {B} }$

wobei

$N_{{\mathrm {B}}}\,$ Minimale Anzahl der Bausteine,

$N_{{\mathrm {Sp}}}\,$ Anzahl an den Reaktionen beteiligten Spezies.

Herleitung

Eine Spezies i, hier geschrieben als $A_{i}$ setzt sich dabei aus den Bausteinen $B_{k}$ folgendermaßen zusammen:

$A_{i}=\sum _{{k=1}}^{{N_{{\mathrm {B}}}}}\beta _{{ik}}B_{k}\quad \Rightarrow \quad \sum _{{i=1}}^{{N_{{\mathrm {Sp}}}}}\nu _{{ij}}\beta _{{ik}}=\underline {\underline {0}}$ .

in die Ratengleichung (Gl.1) eingesetzt und über alle Spezies summiert, liefert wegen $\sum _{{i=1}}^{{N_{{\mathrm {Sp}}}}}{\dot c}_{i}\beta _{{ik}}=0$ die oben genannte Bausteinerhaltung.

Beispiel für die Matrix β_ik

${\begin{pmatrix}\mathrm {H_{2}} \\\mathrm {O_{2}} \\\mathrm {H_{2}O} \\\mathrm {H_{3}O^{+}} \\\mathrm {OH^{-}} \end{pmatrix}}=\underbrace {\begin{pmatrix}2&0&0\\0&2&2\\2&1&1\\3&1&0\\1&1&2\end{pmatrix}} _{\beta _{ik}}\cdot {\begin{pmatrix}\mathrm {H} \\\mathrm {O^{+}} \\e^{-}\end{pmatrix}}$

Basierend auf einem Artikel in:

Wikipedia.de

Ratengleichung

Herleitung

Verschiedene Fälle

Ratenkoeffizenten

Beispiele

Wasserstoffoxidation

Belousov-Zhabotinsky-Reaktion

Lotka-Volterra-Gleichungen

Numerische Lösungsmethoden

Bausteinerhaltung

Herleitung

Beispiel für die Matrix βik

Beispiel für die Matrix β_ik