Kepler-Gleichung
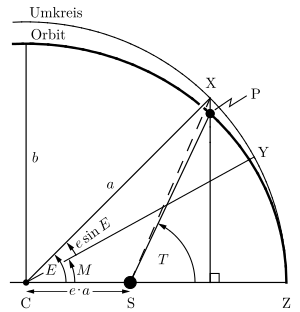
| Punkte: | Winkel: |
|---|---|
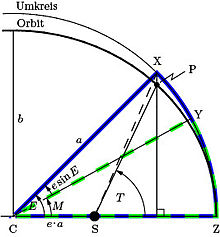
| C: Mittelpunkt | T: Wahre Anomalie |
| S: Brennpunkt | E: Exzentrische Anomalie |
| Z: Periapsis | M: Mittlere Anomalie |
| P: Objekt | |
| X: Hilfspunkt zum Objekt | |
| Y: fiktives Objekt |
Die Kepler-Gleichung ist eine transzendente Gleichung zur Berechnung elliptischer Bahnen von Himmelskörpern. Sie ergibt sich aus den ersten beiden Kepler'schen Gesetzen, die Johannes Kepler 1609 publizierte, und lautet
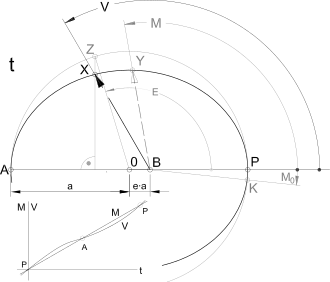
Mit ihr lassen sich die im Kepler-Problem anfallenden Aufgaben lösen. Insbesondere kann der momentane Winkelabstand (wahre Anomalie T) eines Himmelsobjekts P von der Periapsis Z seiner Keplerbahn in Abhängigkeit von der Zeit t ermittelt werden.
Bei der häufigsten, der elliptisch
geformten Keplerbahn wird wie folgt vorgegangen:
Auf einem Umkreis zur
Ellipse werden zwei Punkte definiert: ein dem Himmelsobjekt entsprechender
Punkt X mit sogenannter exzentrischer Anomalie E
und ein fiktiver Punkt Y, der den Ablauf der gleichmäßig vergehenden
Zeit t simuliert und die sogenannte mittlere
Anomalie M besitzt (M proportional zu t). Die
Kepler-Gleichung folgt aus dem zweiten Keplerschen Gesetz. Sie
ist eine Beziehung zwischen den Anomalien E und M, mit deren
Hilfe schließlich die wahre Anomalie T als Funktion der mittleren
Anomalie M oder der Zeit t gefunden werden kann.
Die Kepler-Gleichung kann zum Beispiel bei der Ermittlung der Zeitgleichung angewendet werden. Eine Teilaufgabe dabei ist, die wahre Anomalie der Erde auf ihrer elliptischen Bahn um die Sonne anzugeben.
Herleitung
Mittlere Anomalie
Die gleichmäßig vergehende Zeit lässt sich an der Bewegung eines fiktiven
Körpers auf einer Kreisbahn mit konstanter Winkelgeschwindigkeit
veranschaulichen. Hierfür wird ein Umkreis
als Hilfskreis um die Kepler-Ellipse (Orbit),
auf dem der fiktive Körper Y umläuft, gelegt. Y steht im Zeitpunkt
ebenso wie das wahre Objekt in der Periapsis und hat dieselbe
Umlaufzeit.

Die momentane Lage des Punktes Y wird als Winkel (alle folgenden Winkel werden mit Bogenmaß dargestellt) im Hilfskreis-Mittelpunkt C im Bezug zur Periapsis Z angegeben und als mittlere Anomalie M bezeichnet:
Dabei ist U die Bahnperiode,
und
ist die konstante Winkelgeschwindigkeit. Im Zeitpunkt tP
befindet sich das Himmelsobjekt in der Periapsis (Periapsiszeit),
wobei es den geringsten Abstand zu seinem Schwerezentrum S
hat.
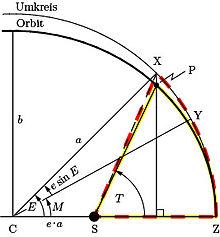
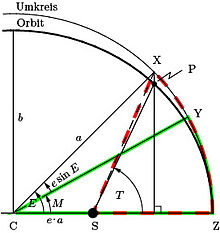
Das Kepler-Problem ist die rechnerische Anwendung des zweiten keplerschen Gesetzes, das heißt die Angabe der Position des Himmelskörpers P (wahre Anomalie) zu einem vorgegebenen Zeitpunkt (mittlere Anomalie). Die gemäß diesem Gesetz in gleich großen Zeitabschnitten gleich großen von der Verbindungslinie zwischen Bahnzentrum und Himmelskörper überstrichenen Flächen lassen sich bei elliptischer Geometrie leichter auf dem Umweg über den Umkreis rechnerisch behandeln. Zwischen Umkreis und Ellipse besteht eine Affinität, die Teilflächen der Ellipse proportionalen Kreissektoren, die einfach zu berechnen sind, zuordnet.
Gemäß dem zweiten keplerschen Gesetz ist der Anteil der elliptischen
Teilfläche an der Ellipse gleich groß wie der Kreissektor am Umkreis. Im
gleichen Zeitabschnitt überstreicht der Fahrstrahl
des Körpers P im Verhältnis die gleich große Fläche wie der
Fahrstrahl
des Punktes Y:
ist die große Halbachse der Ellipse und der Radius des Umkreises,
ist die kleine Halbachse der Ellipse.
ist Ausdruck der Affinität zwischen Umkreis und Ellipse. Letztere ist mit
reziprokem Wert dieses Verhältnisses in jeder Parallele zur kleinen Halbachse
der „gestauchte“ Umkreis.
Exzentrische Anomalie
Durch eine zur kleinen Halbachse parallele Projektion des Punktes P auf den Umkreis entsteht der Hilfspunkt X, dessen Winkel im Mittelpunkt C zur Periapsis Z von Kepler exzentrische Anomalie E genannt wurde. Die Affinität begründet folgenden Zusammenhang:
Nach Einsetzen von Gleichung (2) in Gleichung (3) folgt:
Keplergleichung
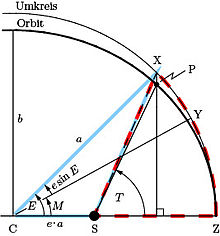
Mit Gleichung (4) ist die gesuchte Beziehung zwischen der exzentrischen Anomalie (Punkt X) und der mittleren Anomalie (Punkt Y) indirekt gefunden. Die direkte Beziehung entsteht durch folgende Schritte:
Wenn der Fahrstrahl
in einer Periode U den Winkel
zurücklegt und die Fläche
überstreicht, so überstreicht er bis zum Zeitpunkt
den Winkel
und eine um den Faktor
kleinere Fläche:
Die analoge Betrachtung für den Fahrstrahl
über den Winkel
ergibt:
Die Fläche CXZ besteht aus den Teilflächen CXS und SXZ:
Die Teilfläche CXS ist ein geradlinig begrenztes Dreieck mit der
Basis
und der Höhe
:
e ist die numerische Exzentrizität der Ellipse, die den Abstand zwischen Mittelpunkt und Brennpunkt im Verhältnis zur großen Halbachse a angibt.
Die Teilfläche SXZ ist nach Gleichung (4) gleich groß wie die Fläche CYZ, deren Wert in Gleichung (5) angegeben ist.
Durch Einsetzen der Gleichungen (6), (8) und (5) wird aus Gleichung (7):
Daraus ergibt sich schließlich die Kepler-Gleichung:
Lösung der Kepler-Gleichung
Die Kepler-Gleichung ist nicht in geschlossener Form nach der exzentrischen
Anomalie
mit ihr aus der mittleren Anomalie
zu ermitteln ist:
1. Die Größe
kann als Nullstelle der Funktion der
Keplergleichung betrachtet werden:
- Die Nullstelle kann etwa mit dem Newton-Verfahren numerisch berechnet werden.
2. Ein stabileres, aber langsamer konvergierendes Verfahren beruht auf dem banachschen Fixpunktsatz:
3. Für kleine Exzentrizität
kann
auch folgendermaßen approximiert
werden:
- Der Fehler ist hierbei von der
Größenordnung
. Bei der Erde und ihrer Exzentrizität
liegt der Fehler für begrenzte Zeiträume hinter der 5. Kommastelle.
Lösung einiger Teilaufgaben im Kepler-Problem
Wahre Anomalie
Für einen Himmelskörper auf einer Keplerbahn ist für den Zeitpunkt
beziehungsweise für die zugehörige mittlere Anomalie
der Ort beziehungsweise die wahre Anomalie
anzugeben. Mit Hilfe der Kepler-Gleichung wird zuerst die exzentrische
Anomalie
ermittelt (siehe oben). Aus Letzterer folgt die wahre Anomalie
nach einer der folgenden Beziehungen:
oder
bzw.
Hier ist
die lineare
Exzentrizität der Bahnellipse. Zum Auflösen nach
ist jeweils eine Unterscheidung der Fälle
und
nötig.
- Bemerkungen
- Der Nenner der zweiten Formel gibt gerade den Abstand
des Himmelsobjekts zum Brennpunkt
an:
- Die Formeln können leicht nach
oder
aufgelöst werden, es ergibt sich:
und
bzw.
Zwischen der wahren Anomalie
der exzentrischen Anomalie
und der mittleren Anomalie
bestehen noch zahlreiche weitere Zusammenhänge,
die in der langen Geschichte der Himmelsmechanik
entwickelt wurden. Insbesondere lässt sich die wahre Anomalie – ohne Umweg
über die Keplergleichung – direkt aus einer speziellen Differenzialgleichung
in
errechnen,
was für numerische Näherungsverfahren von Interesse ist.
Insbesondere kann auch hier die wahre Anomalie T durch die mittlere Anomalie M für kleine Exzentrizitäten genähert werden, es ergibt sich die nützliche Näherung
Die Differenz T − M heißt Mittelpunktsgleichung.
Mittlere Anomalie
Für einen Himmelskörper auf einer Keplerbahn mit der wahren
Anomalie
ist die zugehörende mittlere Anomalie
beziehungsweise der zugehörende Zeitpunkt
anzugeben. Es handelt sich um die zur obigen
umgekehrte Aufgabenstellung.
Ausgehend von
ergibt sich die exzentrische Anomalie zu
Der Lageparameter-Index
bei
ruft den Wert der Arkustangensrelation auf, der
am nächsten liegt (siehe Arkustangens
mit Lageparameter). Die Kepler-Gleichung liefert die
zugehörige mittlere Anomalie
Aus der linearen Gleichung für das Bahnelement folgt schließlich:
- Beispiel
Passagezeiten der vier Erdbahnellipsen-Scheitel:
Die für die Erde gültigen
Bahnelemente sind unter mittlere
Kepler-Elemente angegeben. Die im Verweisartikel verwendete
Zeit T ist in Julianischen Jahrhunderten gerechnet. Hier wird
in Tagen gemessen, sodass die linearen Koeffizienten der Zeit T
durch 36525 zu teilen sind, um
und
zu erhalten. Die sehr langsame Änderung der numerischen Exzentrizität wird
allerdings vernachlässigt (
).
Der Nullpunkt der Zeit T – und damit auch von
–
ist der 1. Januar 2000, 12:00 UTC.
Die wahre Anomalie bei Perihelpassage der Erde im Jahr 2000 ist gleich 360°
(nicht null!), im Jahr 2001 gleich 720° u.s.w.
| Perihel 2000 | Frühlings- Nebenscheitel |
Aphel | Herbst- Nebenscheitel |
Perihel 2001 | |
| Wahre Anomalie |
360 | 450 | 540 | 630 | 720 |
| Zeit |
2,511 | 91,883 | 185,140 | 278,398 | 367,770 |
| Zeitabstand |
89,372 | 93,258 | 93,258 | 89,372 |
Der Abstand zwischen den mittleren Perihelpassagen (anomalistisches
Jahr) beträgt
Die so berechneten mittleren Perihelzeiten können sich um mehrere Tage vom
realen (vor allem mondgestörten) Wert unterscheiden.
Bahnradius
Mit der wahren Anomalie wird die Richtung eines Himmelskörpers auf seiner Keplerbahn für eine Zeit t angegeben. Die zugehörende Entfernung – der Bahnradius – ist wie folgt berechenbar:
- r: Entfernung (Bahnradius)
- a: große Halbachse der Ellipse
- e: numerische Exzentrizität
- T: wahre Anomalie
Bahngeschwindigkeit
Die zeitliche Änderung der wahren Anomalie entspricht der Winkelgeschwindigkeit
in Bezug auf das Gravizentrum. Die Normalkomponente der Geschwindigkeit
folgt also direkt aus
Die Radialgeschwindigkeit ist die Änderung des Bahnradius mit der Zeit:
Für die Bahngeschwindigkeit
oder Orbitalgeschwindigkeit
folgt dann
- v: Bahngeschwindigkeit
- T: wahre Anomalie
- r: Bahnradius
Einfacher lässt sich die Bahngeschwindigkeit über den Hodograph
aus dem Flächensatz ableiten:
- C: spezifischer Drehimpuls als zentrale Kenngröße der Bewegung
- p: Halbparameter als kennzeichnendes Bahnelement
- a: große Halbachse
- b: kleine Halbachse
- C²/p = G·M mit Gravitationskonstante G und Masse M des Zentralkörpers
Daraus folgen die Minimal- und Maximalgeschwindigkeit im Apozentrum und Perizentrum einer Ellipsenbahn:
- e: numerische Exzentrizität
Anwendung der Kepler-Gleichung bei der Zeitgleichung
Die quantitative, also rechnerische Behandlung[1] der Zeitgleichung ist im Wesentlichen – nämlich beim aus der elliptischen Bahnbewegung der Erde resultierenden Zeitgleichungsanteil – eine Anwendung der Kepler-Gleichung. Insbesondere wird damit der Ort der Erde auf ihrer elliptischen Bahn (auch Keplerbahn) zu einem vorgegebenen Zeitpunkt bestimmt.
Definitionen der Zeitgleichung
Erste Definition:
Dem Wert der wahren Ortszeit
(WOZ) bzw. mittleren Ortszeit (MOZ) entspricht der jeweilige Stand der wahren
bzw. einer fiktiven mittleren Sonne am Himmel. Da die Tageszeit im Zusammenhang
mit der Drehung der Erde um ihre Achse steht, interessiert nur die jeweilige Rektaszension (nicht die
Deklination)
der Sonne(n). Anders gesagt: Von den in zwei zueinander rechtwinklig erfolgten
scheinbaren Jahresbewegungen der wahren Sonne interessiert nur die auf dem Himmelsäquator
stattfindende, jedoch nicht das periodische An- und Absteigen. Die die
gleichmäßig vergehende Zeit repräsentierende mittlere Sonne läuft auf dem
Himmelsäquator um. Die Zeitgleichung ist proportional zur Differenz zwischen den
Rektaszensionen
der fiktiven mittleren und
der realen wahren Sonne.
Zweite Definition:
Der Faktor 4 ergibt sich daraus, dass zwei Himmelskörper mit
1° Rektaszensionsdifferenz den Meridian im zeitlichen Abstand von
4 Minuten passieren. Die Reihenfolge der beiden Subtraktionsterme hat sich
umgekehrt, weil die Richtungen für den Stundenwinkel
(ihm entsprechen WOZ und MOZ) und die Rektaszension
zueinander entgegengesetzt definiert sind.
Vorgehensweise
Der zu einem bestimmten Zeitpunkt
zu ermittelnden Rektaszension
(Gleichung (11)) der Sonne entspricht in heliozentrischer Betrachtung die
äquatoriale Länge der Erde, die auf einfache Weise aus ihrer ekliptikalen
Länge
(zweite der nebenstehenden Abbildungen) errechenbar ist. Mit Hilfe der
Kepler-Gleichung wird die wahre Anomalie
(erste der nebenstehenden Abbildungen) ermittelt, aus der dann durch
Bezugspunktänderung
bestimmt wird.
Anwendung der Kepler-Gleichung

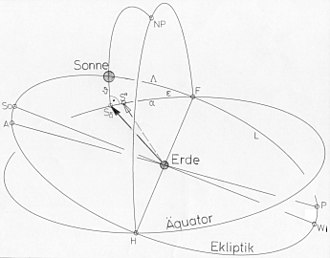
S″: mittere Sonne auf dem Äquator
Mittlere Anomalie:
Die in Gleichung (1) allgemein formulierte mittlere Anomalie lautet im Zusammenhang mit der Zeitgleichung:
: anomalistisches Jahr zwischen zwei Passagen des Perihels
: Zeitpunkt der Perihel-Passage
Bei Periheldurchgang hat die mittlere Anomalie folgenden Wert:
Bei der Zeitgleichung ist es üblich, die Werte eines Kalenderjahres im
entsprechenden Astronomischen
Jahrbuch zu veröffentlichen. Der 1. Januar 12:00 (UT) des
entsprechenden Jahres wird als Nullpunkt für
verwendet, sodass gegenwärtig für
etwa 2 bis 3 Tage und daraus für
etwa 2° bis 3° gelten.[2]
Es hat sich bequemerweise eingebürgert, den jeweils neuen Wert für
als eine sogenannte Jahreskonstante im Voraus zu veröffentlichen.
Mit
und
ab 1. Januar 12:00 (UT) wird aus Gleichung (12):
Kepler-Gleichung:
Mit der dem vorgegebenen Zeitpunkt entsprechenden mittleren
Anomalie
und der Erdbahn-Exzentrizität
wird mit Hilfe der Kepler-Gleichung die exzentrische Anomalie
ermittelt.
Wahre Anomalie:
Bei der Behandlung der Zeitgleichung wird für die wahre Anomalie meistens das
Formelzeichen
(anstatt
wie oben) verwendet.
Die exzentrische Anomalie
führt in einer rein geometrischen Betrachtung in der Ellipse und in ihrem
Umkreis (erste der nebenstehenden Abbildungen) wie folgt zur wahren
Anomalie
:
… eine Ellipsenkonstante
Das Kepler-Problem ist mit der Ermittlung der wahren Anomalie der Erde gelöst. Im Folgenden wird die Ermittlung der Zeitgleichung abgeschlossen.
Wahre Anomalie der Erde → Rektaszension der Sonne
Wahre Anomalie der Erde → ekliptikale Länge der Erde → ekliptikale Länge der Sonne:
Von der Erde aus gesehen spiegelt sich die Bewegung der Erde um die Sonne
wider in der scheinbaren Bewegung der Sonne in der Ekliptik, dem Schnitt der
Erdbahnebene mit der um die Erde als Mittelpunkt geschlagenen Richtungskugel
(siehe zweite der nebenstehenden Abbildungen).[3]
Die ekliptikale Länge der Erde und die ekliptikale Länge der Sonne sind somit
Synonyme mit dem Formelzeichen
Bezugspunkt für die ekliptikale
Länge (und auch der Rektaszension) ist gemäß allgemeinem Brauch der Frühlingspunkt. Die
ekliptikale Länge
der Sonne wird erhalten, indem dem auf das Perihel der Erdbahn bezogenen
Winkel
der Winkel
zwischen Perihel P und dem dem Frühlingspunkt entsprechenden
Ort (F) addiert wird:[4]
Der Wert von
ist negativ. Unter den nahezu konstanten Grundgrößen ist
diejenige, die sich mit der Zeit wegen der langsamen Annäherung zwischen
Frühlingspunkt bzw. Punkt (F) und Perihel am stärksten verändert.
Sie wird deshalb nicht nur jährlich als sogenannte Jahreskonstante
neu gesetzt, sondern mit folgender Gleichung permanent verändert:
Frühlingspunkt und Perihel nähern sich mit ≈
ist das tropische
Jahr (Zeit für zwei aufeinanderfolgende Passagen des Frühlingspunkts bzw.
des Punktes (F)). Unter Beachtung der Gleichung (16) ist
statt Gleichung (15) zu schreiben:
Der Wert von
ist negativ.
Ekliptikale Länge der Sonne → Rektaszension der Sonne:
Neben der Elliptizität der Erdbahn verursacht die zur Erdbahnebene nicht rechtwinklige Lage der Erdachse und ihre Richtungsänderung relativ zur Sonne die Zeitgleichung.
Die Rektaszension
der Sonne lässt sich z.B. mit allgemein bekannten Transformationsgleichungen
oder mit folgender einfachen Beziehung im entsprechenden rechtwinkligen
sphärischen Dreieck (siehe dritte der nebenstehenden Abbildungen) aus der
ekliptikalen Länge
ermitteln:
ist die Schiefe der Erdachse: ε = 23,44°.
Rektaszension der mittleren Sonne
Die Bewegung der mittleren Sonne S″ (dritte der rechts stehenden Abbildungen) auf dem Äquator macht die gleichmäßig vergehende Zeit gleich wie die der auf der Erdbahn umlaufenden fiktiven Erde (Punkt Y) anschaulich. Ihr Lauf ist möglichst eng an den der wahren Sonne zu koppeln, damit sie deren Lauf etwa „mittelt“. Das wurde mit folgender Definition erreicht:
Wenn man die zeitliche Änderung von
vernachlässigt, gilt auch:
Zeitgleichung
Die beiden zur Anwendung der Zeitgleichung (11) erforderlichen
Rektaszensionen
und
sind gefunden.
Rechenbeispiel
Die Zeitgleichung für den 2. April 2015, 12:00 UT (t = 91 Tage) sei zu berechnen.
Die Jahreskonstanten 2015 sind:[5][6]
Die Rechnungen sind:
Die Zeitgleichung hat am 2. April 2015, 12:00 UT den Wert:
Zeitgleichungswerte für die Passage ausgezeichneter Bahnpunkte
Vom Kalender und damit von der Jahreskonstanten
unabhängig sind Zeitgleichungswerte für die Passage ausgezeichneter Punkte durch
die Erde auf ihrer Bahn (beziehungsweise durch die Sonne auf der Ekliptik):
Frühlings-, Sommer-, Herbst- und Winteranfangspunkt, Perihel und Aphel.
| F-Anfang | S-Anfang | H-Anfang | W-Anfang | Perihel | Aphel | |
|---|---|---|---|---|---|---|
| λ/° | 0 | 90 | 180 | 270 | L0 | L0 + 180 |
| ZG/min | −7,44 | −1,74 | +7,48 | +1,70 | −4,50 | −4,50 |
| tP/d **) | 76,234 | 168,990 | 262,641 | 352,485 | 0 | 182,621 |
*) Die Werte gelten für das Jahr 2004 mit L0 = −76,99°
und Jtr = 365,2428 Tage.
**) Die angegebenen Zeiten beziehen sich auf den Periheldurchgang, nicht wie in
obigem
Beispiel auf den 1. Januar 12:00 UT.
Ihre Berechnung ist einfacher, als die für beliebige Zeitpunkte, weil die
Kepler-Gleichung
nicht gelöst werden muss. Von der vorgegebenen ekliptikalen Länge
eines der ausgezeichneten Punkte ist leicht zur wahren (Gl. (15))[7]
und weiter zur exzentrischen Anomalie zu finden. Aus Letzterer folgt mit der
umgestellten Kepler-Gleichung
die mittlere Anomalie, also der Bahnpunkt der fiktiven mittleren Erde. Die
ekliptikale Länge des Perihels[7]
zu Letzterer addiert (Gl. (19)) ist die gesuchte mittlere
Rektaszension
(Minuend
in der Zeitgleichung (11)). Die wahre Rektaszension
(Subtrahend) ist bei den Punkten Frühling bis Winter mit deren ekliptikaler
Länge
identisch. Nur bei den Punkten Perihel und Aphel ergibt die
Koordinatentransformation (Gl. (18)) kleine Werteunterschiede.
Bei der Vorgehensweise, die Berechnung mit einer vorgegebenen ekliptikalen
Länge bzw. einer vorgegebenen wahren Anomalie zu beginnen, erhält man neben der
Zeitgleichung auch die seit der Perihelpassage der Erde vergangene Zeit. Das ist
die Zeit, die die mittlere Anomalie repräsentiert und sie wird aus dem
Zwischenergebnis für die mittlere Anomalie
mit Hilfe der entsprechend umzustellenden Gleichung (12) errechnet.
Diese Vorgehensweise wird gelegentlich auch für die allgemeine Arbeit empfohlen, Zeitgleichungstabellen zu ermitteln.[8] Man erspart sich dabei das aufwändige Lösen der Kepler-Gleichung, findet zu Werten für gewünschte Zeitpunkte aber nur durch Probieren oder bei genügender Ergebnisdichte durch Interpolieren.
Siehe auch
Literatur
- Andreas Guthmann: Einführung in die Himmelsmechanik und Ephemeridenrechnung. BI-Wiss.-Verl., Mannheim 1994, ISBN 3-411-17051-4.
Anmerkungen
- ↑
Die hier verwendeten Formelzeichen sind die
gleichen wie in:
Sonnenuhren-Handbuch, Berechnung der Zeitgleichung. Deutsche Gesellschaft für Chronometrie e.V., Fachkreis Sonnenuhren, 2006, S. 43–49. - ↑ Wegen der Schalttagregelung im Kalender schwanken beide Werte innerhalb der Vierjahresperiode schwach: ΔtP ≈ ¾Tag, ΔM0 ≈ ¾°.
- ↑
Dieser Zusammenhang erlaubt umgekehrt, die
ekliptikale Länge
und den Frühlingspunkt F als Bezugspunkt (sowohl für
als auch für
) auf die Erdbahn zurückzuspiegeln (siehe nebenstehende Abbildung, rechts → links).
- ↑ Zeichen für Winkeldifferenz und Ort in nebenstehender Abbildung in Klammern gesetzt, da Winkel und Ort für den Gebrauch auf der Erdbahn nicht definiert sind.
- ↑
Diese „Basiswerte“ gelten für den 1. Januar
2015 12:00 UT. Ihre langsame Veränderung wird im Folgenden während des
gesamten Jahres 2015 nicht beachtet. Die in dieser Zeit kumulierte Veränderung
schlägt sich erst in den Jahreskonstanten 2016 nieder. Ausnahme ist
L0. Gleichung (8) enthält die permanente Veränderung
L(t).
Die Hochrechnung der Jahreskonstanten erfolgt mit den Basiswerten der Jahre 2000 bzw. 1900 wie folgt (DGC-Handbuch, S. 47):ist die Zahl der Tage seit 1. Januar 2000 12:00 UT;
ist die Zahl der Jahre seit 1900. Bei den Winkeln
und
ist modulo 360° zu rechnen, und sie müssen zwischen −180° und +180° liegen.
- ↑
Die Jahreskonstanten (z.B. für 2015) werden
hier so bezeichnet, weil sie nur für das eine Jahr benutzt werden, auf das sie
sich beziehen. Darüber hinaus gelten sie ohne bedeutsame Einbuße an
Genauigkeit der Zeitgleichung auch für Termine in fernliegenden Jahren
(z.B. für 2050 oder 1950). Die Zeit
nimmt dann entsprechend hohe positive bzw. negative Werte an; das gegebene Rechenschema bleibt aber unverändert anwendbar. Bei der Bestimmung von
und
sind die Nebenwerte des Arkustangens zu verwenden, die
bzw.
am nächsten liegen.
- ↑ a b Dabei wird mit der ekliptikalen Länge L = L0 des Perihels gerechnet, was ausreichend genau und wegen der nicht bekannten Zeit t auch nicht anders möglich ist.
- ↑ Heinz Schilt: Zur Berechnung der mittleren Zeit für Sonnenuhren. Schriften der Freunde alter Uhren, 1990.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.07. 2024