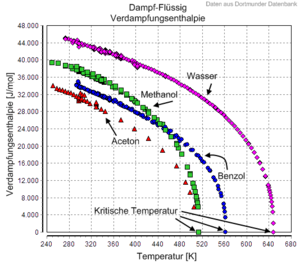
Verdampfungsenthalpie

Die Verdampfungsenthalpie ΔH_v, umgangssprachlich, aber fachsprachlich nicht korrekt auch Verdampfungswärme genannt, ist diejenige Energie, die benötigt wird, um eine bestimmte Menge einer Flüssigkeit zu verdampfen, also vom flüssigen in den gasförmigen Aggregatzustand zu überführen. Die Kondensation (Verflüssigung) als Umkehrung der Verdampfung setzt denselben Betrag an Energie wieder als Kondensationsenthalpie frei. Es handelt sich um eine Form von latenter Wärme.

Die Energie kann dem System in Form von Wärme und/oder Arbeit zugeführt werden. Im offenen System ist die Verdampfung isotherm und isobar, während das Volumen des Stoffs zunimmt. Die Verdampfungsenthalpie ist ein wichtiger Stoffwert in der Dampfdruckkurve. Sie nimmt mit zunehmendem Druck und zunehmender Temperatur ab und wird am sogenannten "Kritischen Punkt" zu Null. Technisch wird die Verdampfungsenthalpie z.B. zur Kühlung angewendet.

Abtrennarbeit

Für den Übergang vom flüssigen in den gasförmigen Aggregatzustand muss – auch falls sich die Flüssigkeit schon am Siedepunkt befindet – Energie in Form von Wärme und/oder Arbeit zugeführt werden. Diese Abtrennarbeit dient zur Überwindung der Anziehungskräfte zwischen den Flüssigkeitsteilchen. Dabei geht die zugeführte Energie aufgrund des Energieerhaltungssatzes nicht verloren, sondern wird zu einem Teil der im Gas gespeicherten und bei der Kondensation wieder frei werdenden Energie.

Bei verflüssigten Edelgasen ist die Abtrennarbeit am kleinsten, da nur Van-der-Waals-Kräfte überwunden werden müssen, bei anderen Flüssigkeiten kommen Dipolmoment oder Wasserstoffbrückenbindung hinzu. Noch höher ist die Verdampfungsenthalpie bei den Metallen (starke metallische Bindung) und am höchsten bei den Salzen wegen der vergleichsweise extrem starken Ionenbindung.

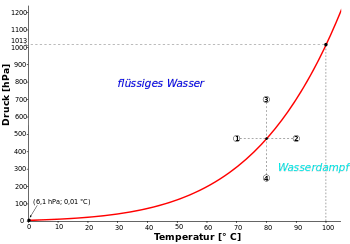
Gleichgewichtsänderung am Beispiel des Wassers

Beispiel: Um ein Kilogramm Wasser bei 100 °C und 1013 mbar zu verdampfen, ist die Abtrennarbeit ΔW = 2088 kJ aufzuwenden. Die Abtrennarbeit ist für Wasser wegen der Wasserstoffbrückenbindungen zwischen den Wassermolekülen relativ hoch.

Verschiebungsarbeit im isobaren Fall

Außerdem hängt der Betrag der zuzuführenden Verdampfungsenthalpie von den Prozessbedingungen ab. Geschieht die Verdampfung oder Verdunstung isobar bei konstantem Druck p, wie es oft der Fall ist, so muss das entstehende Gas, um sich vom Flüssigkeitsvolumen V_F auf das Gasvolumen V_G auszudehnen, gegen den äußeren Druck p die Verschiebungsarbeit leisten. Die zugeführte Energie wird also sowohl für Abtrennarbeit als auch für Verschiebungsarbeit verbraucht:

Beispiel: Bei 100 °C und 1013 mbar hat ein Kilogramm Wasser im flüssigen Zustand ein Volumen von 1,04 dm³ und im gasförmigen Zustand ein Volumen von 1,673 m³. Die Wasser-Konzentration in der Gasphase beträgt bei 100 °C dann 598 g/m³ (siehe Dampfdruckkurve).

Die Volumenzunahme beim Verdampfen beträgt also 1,672 m³ und die bei der Ausdehnung gegen den äußeren Luftdruck geleistete Verschiebungsarbeit 169 kJ. Die unter isobaren Verhältnissen bei 100 °C und 1013 mbar pro kg Wasser zuzuführende Verdampfungsenthalpie beträgt daher ΔH_v = ΔU + p·ΔV = 2088 kJ + 169 kJ = 2257 kJ = 2,257 MJ.

Unter anderen Bedingungen, wie z.B. Verdampfen ins Vakuum, Verdampfen bei konstantem Volumen usw. gelten andere Gesetzmäßigkeiten.

Zugehörige thermodynamische Größen

Zustands- und Prozessgrößen: Enthalpie H, Verdampfungsenthalpie ΔH_v; Druck p, Flüssigkeitsvolumen V_F, Gasvolumen V_G; Verschiebungsarbeit (W =) p ΔV, Volumenänderungsarbeit W_v; Innere Energie U

Die aus den Zustandsgrößen , und gebildete Zustandsgröße

$H=U+p\cdot V$

heißt Enthalpie. Ändern sich , und um die Beträge $\Delta U$ , $\Delta p$ und $\Delta V$ , so ändert sich um den Betrag

$\Delta H=\Delta U+V\cdot \Delta p+p\cdot \Delta V$ .

Bleibt der Druck, wie im hier betrachteten Fall, konstant, so ist

$\Delta H=\Delta U+p\cdot \Delta V$ .

In diesem isobaren Fall ist die zugeführte und auf Abtrenn- sowie Verschiebungsarbeit verteilte Energie

$Q_{v}=\Delta U+p\cdot \Delta V$

also gleich der Enthalpieänderung des Systems

$Q_{v}=\Delta U+p\cdot \Delta V=\Delta H_{v}$

und wird entsprechend Verdampfungsenthalpie ΔH_v genannt.

Beispiel: die Verdampfungsenthalpie von 1 kg Wasser beträgt 2257 kJ (bei 100 °C).

Zahlreiche alltägliche Verdampfungs- und Verdunstungsvorgänge finden im offenen System unter isobaren und isothermen Bedingungen statt, weil die betreffenden Systeme dem atmosphärischen Luftdruck ausgesetzt sind.

Temperaturabhängigkeit der Verdampfungsenthalpie von Wasser, Methanol, Benzol und Aceton

Die stoffspezifische Verdampfungsenthalpie hängt von der Temperatur, nicht dagegen vom äußeren Luftdruck ab. Tabellenwerte finden sich meist für die Siedetemperatur des Stoffes (Dampfdruck des Stoffs ist dann 1013 mbar). Die spezifische Verdampfungsenthalpie bezieht sich auf 1 kg (bzw. 1 g), die molare Verdampfungsenthalpie auf 1 mol des verdampfenden Stoffs.

Für beliebige Temperaturen kann die molare Verdampfungsenthalpie über den gemessenen Dampfdruck (des zu destillierenden Stoffs) mit der Beziehung von Clausius-Clapeyron berechnet werden (Sättigungsdampfdruck).

Temperaturen berechneter Verdampfungsenthalpie für Wasser

Tempe- ratur in °C	Verdampfungs- enthalpie in kJ mol⁻¹	Bemerkung
000	45,054
025	43,990	Standardverdampfungsenthalpie
040	43,350
060	42,482
080	41,585
100	40,657	Normalsiedepunkt
180	36,304	1 MPa (10 bar) Druck
≈ 374	0000	22 MPa, kritischer Punkt

Die molare Verdampfungsenthalpie (in kJ/mol) kann in die spezifische Verdampfungsenthalpie (in kJ/g) umgerechnet werden, indem man sie durch die molare Masse (hier: 18,02 g/mol für Wasser) teilt.

Die molare Verdampfungsenthalpie von Wasser kann im Temperaturbereich von 273 bis 473 K (0 bis 200 °C) durch folgende empirische Formel berechnet werden:

$H_{v}=\left(50{,}09-0{,}9298\cdot {\frac {T}{1000}}-65{,}19\cdot \left({\frac {T}{1000}}\right)^{2}\right)\mathrm {\frac {kJ}{mol}} .$

Kondensationsenthalpie

Kondensiert das Gas unter denselben Bedingungen wieder, so wird die zum Verdampfen aufgewandte Verdampfungsenthalpie in Form der betragsmäßig identischen Kondensationsenthalpie auch wieder frei. Man spricht dann umgangssprachlich davon, dass diese Energie in Form nicht fühlbarer Latentwärme im Gas gespeichert gewesen sei. Dabei handelt es sich jedoch nicht um thermische Energie, sondern um diejenige Energie (Abtrenn- und Verschiebungsarbeit), die bei der Verflüssigung durch die Abnahme des Volumens wieder frei wird.

Sublimationsenthalpie

Bei der Sublimation (Phasenumwandlung von fest nach gasförmig) spricht man von Sublimationsenthalpie, die zusätzlich zur Verdampfungsenthalpie auch die Schmelzenthalpie des Stoffes beinhaltet. Auch Wasser kann sublimieren, daher trocknet Wäsche auch bei Temperaturen unter 0 °C.

Anwendungen

Die Verdampfungsenthalpie wird vor allem zum Wärmetransport genutzt.

Siedekühlung
Funktionsgrundlage des Kühlturms („Rieselkühler“)
stromlos betreibbare „Verdunstungs-Kühlschränke“
Weinkühler
die Kühlung beispielsweise des menschlichen Körpers durch Schwitzen.
Kältemaschine/Wärmepumpe: die Verdampfungsenthalpie wird an der (zu) kühlenden Seite aufgenommen (Verdampfer) und an der (zu) heizenden Seite abgegeben (Kondensation).
Bei der Heizung durch Verbrennung von Kohlenwasserstoffen fällt das Wasser als Reaktionsprodukt der Verbrennung gasförmig an. Dessen Verdampfungsenthalpie ist im Abgas gespeichert. Brennwertkessel kondensieren den Wasserdampf zum größten Teil und gewinnen die dabei frei werdende Kondensationsenthalpie zurück.

Negativbeispiele sind:

Verdunstungskälte:
- weiteres Abkühlen der Autoscheiben bei fahrtwindbegünstigter Verdunstung alkoholhaltiger Schweibenwaschzusätze; daher müssen diese Mischungen für sehr viel tiefere Temperaturen ausgelegt sein als die Außentemperatur im Winter
- Frieren bei nasser Haut oder Kleidung
- Bei der Entnahme von Gas aus Flüssiggasbehältern, wie bei Kohlendioxid, Stickstoff und Propangas, kühlen die Rohrleitungen stark ab und müssen oft zum Beispiel mittels Metallrippen durch Konvektion der Umgebungsluft erwärmt werden.
Kondensationsenthalpie:
- Zur Verflüssigung von Gasen müssen hohe Energiemengen zur Kühlung und/oder zur Erhöhung des Drucks eingesetzt werden, weil Gase unter Umgebungsdruck erst bei sehr niedrigen Temperaturen kondensieren.
- Die Dampfmaschine und auch das Gas- und Dampfkraftwerk (GuD) haben eine um die Verdampfungsenthalpie des Wassers verminderten Wirkungsgrad, weil die Abwärme des Kondensators (falls vorhanden) meist nicht genutzt wird.

Literatur

Roy Bergdoll, Sebastian Breitenbach: Die Roten Hefte, Heft 1 – Verbrennen und Löschen. 18. Auflage. Kohlhammer, Stuttgart 2019, ISBN 978-3-17-026968-2.

Basierend auf einem Artikel in:

Wikipedia.de