Imaginäre Zahl

Eine (rein) imaginäre Zahl (auch Imaginärzahl, lat. numerus imaginarius) ist eine komplexe Zahl, deren Quadrat eine nichtpositive reelle Zahl ist. Äquivalent dazu kann man die imaginären Zahlen als diejenigen komplexen Zahlen definieren, deren Realteil null ist.

Die Bezeichnung „imaginär“ wurde zuerst 1637 von René Descartes benutzt, allerdings für nichtreelle Lösungen von algebraischen Gleichungen. Nach seiner Ansicht gibt es keine Größe, die dem entspricht, man könne sie sich dann bloß einbilden (frz. seulement imaginaires).

Allgemeines

Darstellung einer komplexen Zahl in der Gaußebene

Wie die reellen Zahlen aus der Einheit 1 hervorgehen, basieren die imaginären Zahlen auf der imaginären Einheit $\mathrm {i}$ , einer nichtreellen Zahl mit der Eigenschaft

$\mathrm {i} ^{2}=-1.$

Durch Multiplikation der imaginären Einheit $\mathrm {i}$ mit einem reellen Faktor entsteht mit

$b\cdot \mathrm {i}$

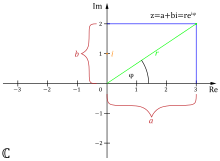
stets eine imaginäre Zahl. Und auch umgekehrt ist jede imaginäre Zahl so ein reelles Vielfaches der imaginären Einheit. In der Gaußebene (siehe Bild) bilden die imaginären Zahlen die mit Im beschriftete Gerade, die die reelle Zahlengerade Re bei der gemeinsamen Zahl 0 rechtwinklig schneidet.

Anwendung

In den imaginären Zahlen lassen sich Gleichungen lösen, die keine reellen Lösungen haben können. Zum Beispiel hat die Gleichung

$x^{2}-4=0$

als Lösung zwei reelle Zahlen, nämlich 2 und −2. Aber die Gleichung

$x^{2}+4=0$

kann keine reelle Lösung haben, da Quadrate reeller Zahlen niemals negativ sind, sodass es keine reelle Zahl gibt, deren Quadrat −4 wäre. Die Lösung dieser Gleichung sind zwei imaginäre Zahlen, $+2\mathrm {i}$ und $-2\mathrm {i}$ .

Eine Beschäftigung mit Quadratwurzeln aus negativen Zahlen wurde bei der Lösung von kubischen Gleichungen im Fall des Casus irreducibilis nötig.

In der komplexen Wechselstromrechnung wird als Symbol für die imaginäre Einheit statt $\mathrm {i}$ ein $\mathrm {j}$ benutzt, um Verwechslungen mit dem Momentanwert i(t) der Stromstärke zu vermeiden. Diese Bezeichnung geht auf Charles P. Steinmetz zurück. Sie ist gemäß DIN 1302, DIN 5483-3 und ISO 80000-2 als Symbol erlaubt.

Rechenregeln

Summen oder Differenzen zweier imaginärer Zahlen sind stets imaginär:

$b\mathrm {i} -c\mathrm {i} =(b-c)\cdot \mathrm {i}$

Produkte oder Quotienten zweier imaginärer Zahlen sind stets reell:

$b\mathrm {i} \cdot c\mathrm {i} =bc\cdot \mathrm {i} ^{2}=-bc$

Potenzen

${\begin{aligned}\mathrm {i} ^{-1}&={\frac {1}{\mathrm {i} }}={\frac {\mathrm {i} }{\mathrm {i} ^{2}}}={\frac {\mathrm {i} }{-1}}=-\mathrm {i} \\\mathrm {i} ^{0}&=1\\\mathrm {i} ^{1}&=\mathrm {i} \\\mathrm {i} ^{2}&=-1\\\mathrm {i} ^{3}&=\mathrm {i} ^{2}\cdot \mathrm {i} =-\mathrm {i} \\\mathrm {i} ^{4}&=\mathrm {i} ^{2}\cdot \mathrm {i} ^{2}=(-1)^{2}=1\end{aligned}}$

allgemein:

${\begin{aligned}\mathrm {i} ^{4n}&=1\\\mathrm {i} ^{4n+1}&=\mathrm {i} \\\mathrm {i} ^{4n+2}&=-1\\\mathrm {i} ^{4n+3}&=-\mathrm {i} \\\mathrm {i} ^{2n}&=(\mathrm {i} ^{2})^{n}=(-1)^{n}\end{aligned}}$

für alle $n\in \Z$ .

Komplexe Zahlen

→ Hauptartikel: Komplexe Zahl

Die imaginäre Einheit $\mathrm {i}$ erlaubt die Erweiterung des Körpers der reellen Zahlen zum Körper der komplexen Zahlen.

Heute versteht man imaginäre Zahlen als spezielle komplexe Zahlen. Jede komplexe Zahl kann dargestellt werden als Summe einer reellen Zahl und eines reellen Vielfachen der imaginären Einheit $\mathrm {i}$ .

Algebraisch wird $\mathrm {i}$ definiert als eine Nullstelle des Polynoms x^2 + 1 und die komplexen Zahlen als die dadurch erzeugte Körpererweiterung. Die zweite Nullstelle ist dann $-\mathrm{i}$ . Man kann die beiden Nullstellen erst unterscheiden, wenn man eine der beiden mit $\mathrm {i}$ bezeichnet hat. Für die beiden Nullstellen hat man hierbei keine Unterscheidungsmerkmale. Es spielt so keine Rolle, „welche“ Nullstelle man nun mit $\mathrm {i}$ bezeichnet. (Wird jedoch, wie üblich, der komplexe Zahlenbereich auf der Struktur des $\mathbb {R} ^{2}$ definiert statt nur mit seiner Hilfe dargestellt, so kann man die möglichen Nullstellen sehr wohl unterscheiden und wählt naheliegenderweise $\mathrm {i} :=(0,1)^{\mathrm {T} }$ statt des ebenso möglichen $\mathrm {i} :=(0,-1)^{\mathrm {T} }$ .)

Alle komplexen Zahlen lassen sich in der Gaußebene darstellen, einer Erweiterung der reellen Zahlengeraden. Die komplexe Zahl $a+\mathrm {i} \cdot b$ mit reellen Zahlen a,b hat den Realteil und den Imaginärteil . Aufgrund der Rechenregeln komplexer Zahlen ist das Quadrat einer Zahl, deren Realteil gleich 0 ist, eine nichtpositive reelle Zahl:

$(b\,{\mathrm i})^{2}=-b^{2}$

Weiteres

Erweiterungen stellen die hyperkomplexen Zahlen dar, die über die komplexen Zahlen hinausgehend mehrere imaginäre Einheiten aufweisen. Beispielsweise treten bei den vierdimensionalen Quaternionen drei imaginäre Einheiten auf, bei den achtdimensionalen Oktonionen gibt es sieben imaginäre Einheiten.

In der eulerschen Identität wird ein prägnanter, einfacher Zusammenhang der imaginären Einheit $\mathrm {i}$ mit drei anderen grundlegenden mathematischen Konstanten hergestellt, nämlich mit der eulerschen Zahl $\mathrm {e}$ , der Kreiszahl $\mathrm {\pi }$ sowie der reellen Einheit 1:

$\mathrm {e} ^{\mathrm {i} \,\pi }=-1$

Literatur

Ilja N. Bronstein, K. A. Semendjajew, Gerhard Musiol, Heiner Muehlig: Taschenbuch der Mathematik. 7. Auflage. Harri Deutsch, 2008, ISBN 978-3-8171-2007-9.

Basierend auf einem Artikel in:

Wikipedia.de