Renormierungsgruppe

Die Renormierungsgruppe (RG) beschreibt die Abhängigkeit bestimmter physikalischer Größen von der Längenskala. Ursprünglich ein Konzept der Quantenfeldtheorie, erstreckt sich sein Anwendungsbereich heutzutage auch auf die Festkörperphysik, Kontinuumsmechanik, Kosmologie und Nanotechnologie. Mit der RG im Zusammenhang stehen die Betafunktion und die Callan-Symanzik-Gleichungen.

Definition

Als Renormierungsgruppe bezeichnet man mehrere ähnliche aber im Detail verschiedene Rechenverfahren, die von einer Skaleninvarianz des beschriebenen Systems Gebrauch machen. Die untersuchten Systeme sind dabei alle stochastischer Natur. Bei Systemen aus der Quantenfeldtheorie beruht die stochastische Natur auf Quantenfluktuationen, bei Systemen aus der klassischen Physik auf thermischen Fluktuationen, Wahrscheinlichkeiten für Verunreinigungen, oder Übergangswahrscheinlichkeiten für irgendwelcher Reaktionen. Ein anschauliches (eher mathematisches) Beispiel ist die Perkolation. In aller Regel ist das Problem als Pfadintegral vorgegeben, und die interessierenden Messgrößen sind Korrelationsfunktionen oder davon abgeleitete Größen.

Die Idee einer Renormierungsgruppen-Rechnung ist, das ursprüngliche (nicht renormierte) System entsprechend einer genau definierten Vorschrift auf sogenannte renormierte Systeme abzubilden. Bei dieser Abbildung ist immer eine andere (i.d.R. variable) Längenskala im Spiel, indem explizit Skalierungen ausgeführt werden oder/und Vertexfunktionen bei gewissen Längenskalen berechnet werden.

Falls das renormierte System einfacher ist, indem es z.B. bei einer Änderung der Längenskala einen Fixpunkt erreicht oder die Kopplungskonstanten klein werden, hat man wegen der eindeutigen Abbildung (zumindest für gewisse Längenskalen) damit auch für das eigentlich interessierende Problem viel gewonnen. Dass der Formalismus auch eine anschauliche Interpretation im Sinne von skalenabhängigen Kopplungskonstanten hat, ist essentiell und instruktiv, für die Anwendung des Formalismus selber spielt das keine Rolle.

Die Bedeutung von Renormierungsgruppen-Rechnungen liegt darin, dass sie oft nach Schema anwendbar sind und Ergebnisse liefern, wo andere Methoden nicht weiterführen. Beispielsweise liefert naive (regularisierte) Störungsrechnung in der Quantenfeldtheorie und bei kritischen Phänomenen eine divergente Störungsreihe, während die Renormierungsgruppe implizit Störungsrechnungsbeiträge aufsummiert und die Skaleninvarianz korrekt zum Ausdruck bringt.

Einfachster Zugang: Kadanoffs Blockspin-Modell

Kadanoffs Blockspin

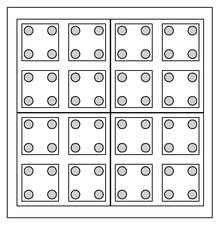
Das Blockspin-Modell von Leo Kadanoff (1966) liefert den didaktisch einfachsten Zugang zur RG. Dazu betrachtet man ein zweidimensionales Gitter von Spin -Freiheitsgraden (das kann aber auch ein Modell für Gitter von Atomen mit ganz anderen Freiheitsgraden als Drehimpulsen sein) vom Typ des Isingmodells, das heißt, es wechselwirken nur unmittelbar benachbarte Spins miteinander mit einer Kopplungsstärke $\, J$ . Das System werde durch eine Hamiltonfunktion $\, H(T,J)$ beschrieben und habe die mittlere Temperatur $\,T$ .

Nun wird das Spin-Gitter in Blöcke von $2\times 2$ - Quadraten aufgeteilt und es werden neue Blockvariable eingeführt, indem über die Zustandswerte im Block gemittelt wird. Häufig hat die neue Hamiltonfunktion die gleiche Struktur wie die alte, nur mit neuen Werten für $\,T$ und $\,J$ : $\quad H(T,J)\to H(T',J')$ .

Dieser Vorgang wird nun wiederholt, das heißt man fasst wieder $2\times 2$ der neuen Spin-Blockvariablen durch Mittelung zusammen (das wären dann jeweils 4 Spins oder 16 Spins aus dem Ausgangsmodell) usw. Das System wird also auf einer ständig vergröbernden Skala betrachtet. Ändern sich dabei die Parameter unter RG-Transformationen nicht mehr wesentlich, spricht man von einem Fixpunkt der RG.

Im konkreten Fall des Isingmodells, ursprünglich als Modell für magnetische Systeme eingeführt (mit einer Wechselwirkung, die bei parallelen Spins einen negativen Beitrag, $- \,J$ , zur Energie liefert, bei anti-parallelen Spins einen positiven Beitrag $\, J$ ), wirkt die durch die Temperatur $\,T$ gekennzeichnete Wärmebewegung den Ordnungsbestrebungen der Wechselwirkung (durch $\, J$ charakterisiert) entgegen. Hier (und häufig auch in ähnlichen Modellen) gibt es drei Arten von Fixpunkten der RG:

(a) $\,T=0$ und $\,J\to\infty$ . Auf großen Skalen überwiegt die Ordnung, ferromagnetische Phase.

(b) $\,T\to\infty$ und $\,J\to 0$ . Unordnung auf großen Skalen.

(c) Ein Punkt dazwischen mit $\,T = T_c$ und $\,J = J_c$ , bei dem eine Skalenänderung die Physik des Systems nicht verändert (Skaleninvarianz wie in fraktalen Strukturen), der Punkt ist ein Fixpunkt der RG. An diesem sogenannten kritischen Punkt findet ein Phasenübergang zwischen den beiden Phasen (a), (b) statt. Im Fall des Ferromagnetismus wird er Curie-Punkt genannt.

Elemente der RG-Theorie

Allgemein sei das System durch eine Funktion $\, Z$ der Zustandsvariablen $\, \{s_i\}$ mit den Wechselwirkung beschreibenden Kopplungskonstanten $\, \{J_k\}$ beschrieben. Je nach Anwendungsbereich kann das eine Verteilungsfunktion (statistische Mechanik), eine Wirkung, eine Hamiltonfunktion u.a. sein, sollte aber die Physik des Systems vollständig beschreiben.

Nun betrachten wir Block-Transformationen der Zustandsvariablen $\{s_i\}\to \{\tilde s_i\}$ , wobei die Anzahl der $\tilde s_i$ kleiner als die der $\, s_i$ ist. Man versucht nun $\, Z$ allein als Funktion der neuen Zustandsvariablen $\tilde s_i$ zu schreiben. Ist dies allein durch eine Änderung der Parameter der Theorie $\{J_k\}\to \{\tilde J_k\}$ möglich, spricht man von einer renormierbaren Theorie.

Die meisten grundlegenden Theorien der Elementarteilchenphysik, wie Quantenelektrodynamik, Quantenchromodynamik, die elektroschwache Wechselwirkung, sind renormierbar (die Gravitation allerdings nicht). Auch in der Festkörperphysik und Kontinuumsphysik sind viele Theorien (näherungsweise) renormierbar (z.B. Supraleitung, Theorie der Turbulenz von Flüssigkeiten).

Die Änderung der Parameter erfolgt durch eine sogenannte Betafunktion ${\tilde {J}}_{k}=\beta (J_{i})$ , die einen Fluss der RG (RG flow) im -Raum erzeugt. Die Veränderung von unter diesem Fluss wird mit dem Begriff gleitende Kopplungskonstante (running coupling constant) beschrieben. Man ist vor allem an den Fixpunkten des RG-Flusses interessiert, die Phasenübergänge zwischen den makroskopischen Phasen des Systems beschreiben.

Da bei den RG-Transformationen ständig Information verlorengeht, haben sie im Allgemeinen keine Inverse und bilden somit eigentlich auch keine Gruppen im mathematischen Sinn (sondern nur Halbgruppen). Der Name Renormierungsgruppe hat sich trotzdem eingebürgert.

Relevante und irrelevante Operatoren, Universalitätsklassen

Man betrachte das Verhalten der Observablen (in der Quantenmechanik durch Operatoren gegeben) unter einer RG-Transformation:

falls bei Übergang zu größeren Skalen stets zunimmt, spricht man von relevanten Observablen
falls bei Übergang zu größeren Skalen stets abnimmt, spricht man von irrelevanten Observablen und
falls keins von beidem zutrifft, spricht man von marginalen Observablen.

Für das makroskopische Verhalten sind nur relevante Operatoren wichtig, und in der Praxis stellt sich heraus, dass in typischen Systemen nach hinreichend vielen Renormierungsschritten nur ganz wenige Operatoren „übrig bleiben“, da nur sie relevant sind (obwohl man es oft mit unendlich vielen Operatoren zu tun hat, so ist auf mikroskopischer Basis typischerweise die Zahl der Observablen von der Größenordnung der Zahl der Moleküle in einem Mol).

Dies erklärt auch die erstaunliche Ähnlichkeit der kritischen Exponenten untereinander in den verschiedensten Systemen mit Phasenübergängen zweiter Ordnung, ob es sich nun um magnetische Systeme, Supraflüssigkeiten oder Legierungen handelt: werden die Systeme durch die gleiche Anzahl und die gleichen Typen (bezüglich des Skalierungsverhaltens) relevanter Observabler beschrieben, gehören sie zur selben Universalitätsklasse.

Diese quantitative und qualitative Begründung der Unterteilung des Phasenübergangsverhaltens in Universalitätsklassen war einer der Haupterfolge der RG.

Impulsraum-RG

In der praktischen Anwendung gibt es zwei Typen von RG: die RG im Ortsraum (Real Space RG), wie sie oben in Kadanoffs Blockspin-Bild diskutiert wurde, und die Impulsraum-RG, bei der das System in verschiedenen Wellenlängen bzw. Frequenzskalen betrachtet wird. Dabei wird meist eine Art Integration über die Moden hoher Frequenz bzw. kurzer Wellenlänge durchgeführt. In dieser Form wurde die RG ursprünglich in der Teilchenphysik angewandt. Da man meist von einer Störungstheorie um das System freier Teilchen ausgeht, funktioniert dies für stark korrelierte Systeme meist nicht mehr.

Ein Beispiel für die Anwendung der Impulsraum-RG ist die klassische Renormierung der Masse und Ladung der freien Teilchen in der QED. Eine nackte positive Ladung ist in dieser Theorie von einer Wolke von ständig aus dem Vakuum erzeugten und gleich wieder vernichteten Elektron-Positron Paaren umgeben. Da die Positronen von der Ladung abgestoßen, die Elektronen angezogen werden, wird die Ladung im Endeffekt abgeschirmt, und die Größe der beobachteten Ladung hängt davon ab, wie nah man ihr kommt (gleitende Kopplungskonstante), bzw. im fouriertransformierten Bild, auf welcher Impulsskala man sich bewegt.

Feldtheoretische Renormierungsgruppe, technische Aspekte

Die am weitesten verbreitete Variante der Renormierungsgruppe hat ihren Ursprung in der Quantenfeldtheorie und ist ein Grundpfeiler der theoretischen Physik, mit vielen Anwendungen auch in anderen Bereichen. Der Ausgangspunkt dabei ist eine Lagrange-Funktion für eine Feldtheorie und das entsprechende Pfadintegral. Eine Anzahl von technischen Aspekten ergeben in Kombination eine große Vielfalt. Beispiele sind

Regularisierung. Eine Regularisierung ist erforderlich da Störungsreihenterme sonst divergieren. Die Vorstellung heute ist, dass es auch in der Quantenfeldtheorie faktisch so etwas wie einen Cutoff gibt, z.B. bei der Planck-Länge. In der Praxis ist i.d.R. dimensionelle Regularisierung das Mittel der Wahl.
Verschiedene Herleitungen. Multiplikative oder additive Renormierung.
Renormierungsbedingungen oder minimale Subtraktion.
Betrachtung nur des kritischen Punktes oder Berücksichtigung relevanter und irrelevanter Terme (Massenterme, externe Felder, Annäherung an den kritischen Punkt).
Unterschied zwischen Quantenfeldtheorie (Limes kleiner Wellenlängen) und Festkörperphysik (Limes großer Wellenlängen)
Skaleninvarianz bei der kritischen Dimension $d_{c}$ oder unterhalb der kritischen Dimension. Entwicklung nach $\varepsilon =d-d_{c}$ oder numerische Rechnung direkt bei $d<d_{c}$ .

Trotz der Vielfalt ist die Rechentechnik in ihrer Essenz immer dieselbe. Die wesentlichen technischen Punkte lassen sich am einfachsten Beispiel verstehen.

Die Essenz anhand eines Beispiels

Ausgangspunkt ist die Lagrangefunktion des $\varphi ^{4}$ -Modells bei der kritischen Temperatur (ohne Massenterm $\propto \varphi ^{2}$ und ohne Magnetfeldterm $\propto \varphi$ )

$L=\int d^{d}x\left\{ \frac{1}{2}\left(\nabla\varphi\right)^{2}+\frac{u}{4!}\varphi^{4}\right\}.$

Als eine Summe von Monomen kann die Lagrangefunktion invariant unter einer Reskalierung der Felder, der Koordinaten, und der Kopplungskonstanten mit einem beliebigen Skalenfaktor , sein. Hier ist das

${\begin{aligned}x&\rightarrow x/b,\\\varphi &\rightarrow \varphi b^{\left[\varphi \right]},\\u&\rightarrow ub^{\left[u\right]}.\end{aligned}}$

Per Konvention wird als Reskalierungs-Exponent für die Koordinaten immer $[x]=-1$ verwendet. Die beiden Terme der Lagrangefunktion liefern damit zwei Gleichungen aus denen sich die Skalierungsexponenten $[\varphi ]=1-\varepsilon /2$ und $[u]=\varepsilon$ ergeben. Hierbei ist $\varepsilon =d-d_{c}$ mit (oberer) kritischer Dimension $d_{c}=4$ . Zu beachten ist, dass die Kopplungskonstante bei der kritischen Dimension dimensionslos ist.

Die Skaleninvarianz der Lagrangefunktion bei der kritischen Dimension $d_{c}$ impliziert nicht direkt eine Skaleninvarianz der physikalischen Größen, denn diese bestimmen sich aus dem Pfadintegral mit der Lagrangefunktion im Exponenten. Damit das Pfadintegral einen Sinn ergibt ist eine Regularisierung erforderlich, womit implizit eine weitere Längenskala ins Spiel kommt. Das regularisierte Pfadintegral liefert die physikalischen Größen. Die naive Skaleninvarianz der Lagrangefunktion wird i.A. durch Fluktuationen zumindest modifiziert. Ein generischer Ausgangspunkt der Renormierungsgruppe ist die Annahme, dass die Skaleninvarianz in modifizierter Form asymptotisch bestehen bleibt, d.h., dass die 2- und 4-Punkt-Vertexfunktionen der effektiven Lagrangefunktion ebenfalls skaleninvariant sind, wenn auch mit modifizierten Skalenexponenten. Per Konvention schreibt man den Skalenexponenten von $\varphi$ in der Form $[\varphi ]=1-\varepsilon /2+\eta /2$ , wobei $\eta$ auch als kritischer Exponent bezeichnet wird.

Durch "Entfernen" der nichttrivialen Anteile der Skalenexponenten von den Vertexfunktionen $\Gamma_2$ und $\Gamma _{4}$ mit einem Feld-Renormierungsfaktor $Z=(k/\mu _{0})^{\eta }$ erhält man die "renormierten" Vertexfunktionen,

${\begin{aligned}\Gamma _{2}^{\left(R\right)}\left(k,u\right)&=Z\,\Gamma _{2}\left(k,u\right),\\\Gamma _{4}^{\left(R\right)}\left(k,u\right)&=Z^{2}\Gamma _{4}\left(k,u\right).\end{aligned}}$

Der konstante Wellenvektor $\mu _{0}$ ist aus Dimensionsgründen eingeführt. Die Vertexfunktion $\Gamma _{4}$ hängt eigentlich von 3 Wellenvektoren ab, aber zum Zweck der Renormierung ist es ausreichend, eine symmetrische Situation zu betrachten, wo die drei Wellenvektoren von den Ecken eines Tetraeders zum Mittelpunkt zeigen und denselben Betrag haben (auch andere Konventionen sind möglich).

Die Störungsrechnung liefert für die Vertexfunktionen $\Gamma_2$ und $\Gamma _{4}$ Potenzreihen in der nicht renormierten dimensionslosen Kopplungskonstante ${\bar {u}}=uk^{-\varepsilon }$ . Diese Potenzreihen sind am kritischen Punkt, d.h. bei $k\to 0$ divergent und zunächst nutzlos. Der nächste Schritt ist das Aufstellen der Normierungsbedingung

$\frac{\partial}{\partial k^{2}}\Gamma_{2}^{\left(R\right)}\left(k,u\right)=1.$

Daraus bestimmt sich im Prinzip der Faktor als Potenzreihe in $\bar{u}$ . Der Clou der ganzen Aktion ist die Definition einer dimensionslosen renormierten Kopplungskonstante

$u_{R}\left(\bar{u}\right)=k^{-\epsilon}\Gamma_{4}^{\left(R\right)}\left(k,u\right).$

Diese dimensionslose renormierte Kopplungskonstante ändert sich als Funktion des Wellenvektors i.d.R. nur langsam, ist oft klein und strebt u.U. gegen einen Fixpunkt. Der Trick ist daher, die Potenzreihen in $\bar{u}$ zu Potenzreihen in u_R zu transformieren. D.h. man ermittelt die Umkehrfunktion ${\bar {u}}(u_{R})$ . Eine entscheidende Rolle spielt dann der Fluss

$k\left(\frac{du_{R}}{dk}\right)_{u}=\beta\left(u_{R}\right)$

der renormierten Kopplungskonstante bei Änderung der Längenskala bei konstantem . Die Bedingung $\beta (u_{R})=0$ liefert ggf. den Fixpunkt der renormierten Kopplungskonstante u_R . Mit u_R und kennt man dann natürlich auch die physikalischen Größen $\Gamma_2$ und $\Gamma _{4}$ .

Anmerkungen

Es ist keineswegs selbstverständlich, dass das beschriebene Rechenverfahren funktioniert. Eine Grundvoraussetzung ist die Skaleninvarianz der Lagrangefunktion bei der kritischen Dimension.
In der Festkörperphysik interessiert der Limes $k\to 0$ , in der Quantenfeldtheorie der Limes $k \to \infty$ .
In der Quantenfeldtheorie interessiert der Fall $d=d_{c}=4$ , d.h. der Limes $\varepsilon \to 0$ . In diesem Fall verschwinden die kritischen Exponenten, es verbleiben aber logarithmische Skalierungs-Faktoren.
Das Beispiel enthält einige willkürlich erscheinende Konventionen. Das kritische Verhalten ist davon unabhängig (Universalität).
Die feldtheoretische Renormierungsgruppe ermöglicht systematische Reihenentwicklungen nach den renormierten Kopplungskonstanten. Die Potenzreihen sind nur asymptotisch konvergent, aber bei kleinen Kopplungskonstanten ist das oft ausreichend.
Physikalische Größen lassen sich ggf. als Potenzreihe in $\varepsilon$ oder (numerisch) direkt bei gegebener Dimension erhalten (etwa für ).
Weitere Felder oder z.B. ein Massenterm in der Lagrangefunktion erfordern weitere -Faktoren.
Die Algebra vereinfacht sich wenn man in der Lagrangefunktion durch $u/K_{d}$ ersetzt mit $K_{d}=2^{-d+1}\pi ^{-d/2}/\Gamma (d/2)$ .

Funktionale Renormierungsgruppe

Eine funktionale Renormierungsgruppe (FRG) ist eine Methode zur Berechnung des effektiven Potentials einer Feldtheorie für eine variable Längenskala. Eine FRG berücksichtigt relevante, marginale und irrelevante Kopplungen. Eine exakte Bestimmung des effektiven Potentials ist damit allerdings i.d.R. genauso wenig möglich wie mit anderen Techniken. Jedoch erlaubt eine FRG verschiedenste Parametrisierungen und ist unabhängig von (nur asymptotisch konvergenten) Störungsreihen-Entwicklungen.

Es gibt mindestens drei FRG-Varianten, eine nach Art der Wilsonschen-Eliminations-Renormierungsgruppe (Wegner und Houghten), eine Variante mit variablem UV-Cutoff (Polchinski) und eine Variante mit einem Infrarot-Regulator (Wetterich). Am einfachsten zu handhaben ist die Variante mit IR-Regulator.

Für die FRG mit IR-Regulator lässt sich im Rahmen der Quantenfeldtheorie mit wenigen formalen Schritten eine kompakte Formel herleiten, die Ausgangspunkt für konkrete Anwendungen ist (Wetterich). Um die Schreibweise zu vereinfachen empfiehlt sich dabei die de-Witt-Schreibweise, wo das Feld $\varphi$ ein Vektor ist, dessen Index einen Punkt im Raum und ggf. auch einen Feldindex spezifiziert. Der erste Schritt besteht darin, zur Wirkung einen Regulator-Term

$S_{R}\left(\mu \right)={\frac {1}{2}}\varphi \cdot R\left(\mu \right)\cdot \varphi$

hinzuzufügen, wo die Matrix von einer Wellenvektor-Skala $\mu$ abhängt (Beispiele weiter unten). Die erzeugende Funktion der zusammenhängenden Korrelationsfunktionen lautet dann

$W\left(J,\mu \right)=\ln \int {\mathcal {D}}\varphi \exp \left(-S-S_{R}\left(\mu \right)+J\cdot \varphi \right),$

wo ein externes Feld bezeichnet. Der Erwartungswert von $\varphi$ ist $\overline{\varphi}_{a}=\partial W/\partial J_{a}$ , und die 2-Punkt-Korrelationsfunktion ist gegeben durch

$\widetilde{G}_{a,b}\left(\mu\right)=\frac{\partial^2 W \left(J,\mu\right)}{\partial J_{a}\partial J_{b}} =\left\langle \varphi_{a}\varphi_{b}\right\rangle -\overline{\varphi}_{a}\overline{\varphi}_{b}.$

Die erzeugende Funktion der 1-Teilchen-irreduziblen Vertex-Funktionen $\widetilde{\Gamma}\left(\mu,\overline{\varphi}\right)$ ist nach üblichem Schema die Legendre-Transformierte

${\widetilde {\Gamma }}\left({\overline {\varphi }},\mu \right)=J\cdot {\overline {\varphi }}-W\left(J,\mu \right).$

Differenzieren nach der Wellenvektor-Skala $\mu$ und Verwenden der Definition von $\widetilde{G}_{a,b}$ führt auf

${\frac {\partial }{\partial \mu }}{\widetilde {\Gamma }}=-{\frac {\partial }{\partial \mu }}W={\frac {\partial }{\partial \mu }}\left\langle S_{R}\left(\mu \right)\right\rangle ={\frac {1}{2}}{\frac {\partial }{\partial \mu }}\left\langle \varphi _{a}R_{a,b}\varphi _{b}\right\rangle ={\frac {1}{2}}\left({\widetilde {G}}_{a,b}+{\overline {\varphi }}_{a}{\overline {\varphi }}_{b}\right){\frac {\partial }{\partial \mu }}R_{a,b}.$

Die Renormierungsgruppen-Differenzialgleichung folgt daraus als

$\mu\frac{\partial}{\partial\mu}\Gamma\left(\overline{\varphi},\mu\right)=\frac{1}{2}Tr\left(\left(\Gamma_{a,b}^{\left(2\right)}\left(\overline{\varphi},\mu\right)+R_{a,b}\right)^{-1}\mu\frac{\partial}{\partial\mu}R_{a,b}\right),$

wo $\Gamma ={\widetilde {\Gamma }}-{\frac {1}{2}}{\overline {\varphi }}\cdot R\cdot {\overline {\varphi }}$ das effektive Potential ohne das künstliche $S_{R}$ bezeichnet und der Propagator $\widetilde{G}=1/\widetilde{\Gamma}_{2}=1/\left(\Gamma_{2}+R\right)$ ebenfalls in einer Form geschrieben ist, die den künstlichen Beitrag $S_{R}$ explizit macht. $Tr\left(\dots\right)$ steht für die Spur einer Matrix.

Der Sinn und die Interpretation der FRG-Differentialgleichung ergeben sich mit der Wahl des Regulators , d.h. des Propagators. Typische IR-Cutoff-Funktionen (ausgedrückt im -Raum) sind $R\left(\mu,k\right)=k^{2}/\left(e^{k^{2}/\mu^{2}}-1\right)$ oder $R\left(\mu,k\right)=\left(\mu^{2}-k^{2}\right)\theta\left(\mu^{2}-k^{2}\right)$ . Diese Funktionen verschwinden schnell für $k\gg\mu$ und erreichen für $k\ll\mu$ den Wert $\mu^2$ . Dies bedeutet, dass Freiheitsgrade mit kurzen Wellenlängen keine Änderung erfahren während Freiheitsgrade mit langen Wellenlängen eine endliche Masse erhalten und unterdrückt werden. Die FRG-Differentialgleichung beschreibt bei $\mu\rightarrow0$ was geschieht, wenn man mehr und mehr Freiheitsgrade mit langen Wellenlängen hinzunimmt. Z.B. kann man auf diese Weise einen kritischen Punkt erreichen, bei dem beliebig lange Wellenlängen zu berücksichtigen sind.

Geschichte der RG

Skalierungsüberlegungen gibt es in der Physik schon seit dem Altertum und an prominenter Stelle z.B. bei Galilei. Die RG tauchte zum ersten Mal 1953 in der Behandlung der Renormierung in der Quantenelektrodynamik durch E. C. G. Stueckelberg und André Petermann sowie 1954 durch Murray Gell-Mann und Francis Low auf. Die Theorie wurde von den russischen Physikern N. N. Bogoljubow und D. V. Shirkov ausgebaut, die 1959 ein Lehrbuch darüber schrieben.

Ein wirkliches physikalisches Verständnis wurde jedoch erst durch die Arbeiten von Leo Kadanoff 1966 erreicht (Blockspin-Transformation), die dann vom Nobelpreisträger (1982) Kenneth Wilson 1971 erfolgreich für die Behandlung sog. kritischer Phänomene in der Umgebung von kontinuierlichen Phasenübergängen und ferner 1974 zur sukzessiv-konstruktiven Lösung des Kondo-Problems benutzt wurden. Er erhielt unter anderem für die erstgenannte Leistung 1982 den Nobelpreis. Auch die alte RG der Teilchenphysik wurde um 1970 von Curtis Callan und Kurt Symanzik neu formuliert. In der Teilchenphysik wurde hauptsächlich die Impulsraum-RG verwendet und ausgebaut. Sie fand auch weite Verwendung in der Festkörperphysik, war aber bei stark korrelierten Systemen nicht anwendbar. Hier war man ab den 1980er Jahren mit Ortsraum-RG-Verfahren erfolgreicher, wie der von Steven R. White (1992) eingeführten Dichtematrix-RG (density matrix RG, DMRG).

Literatur

E. C. G. Stueckelberg und A. Petermann: La renormalisation des constants dans la theorie de quanta. In: Helvetica physica acta. Band 26, 1953 S. 499.
M. Gell-Mann und F. E. Low: Quantum Electrodynamics at small distances. In: Physical Review. Band 95, 1954, S. 1300. (Einführung des Konzepts durch Stueckelberg/Peterman und Gell-Mann/Low)
N. N. Bogoliubov und D. V. Shirkov: The theory of quantized fields. Interscience, 1959. (erste Lehrbuchbehandlung)
L. P. Kadanoff: Scaling laws for Ising models near . In: Physics (Long Island City, N.Y.) Band 2, 1966, S. 263. (das Bild der Block-Spin Transformationen)
K.G. Wilson: Die Renormierungsgruppe. In: Spektrum der Wissenschaft. Oktober 1979.
Daniel J. Amit: Field theory, the renormalization group, and critical phenomena. World Scientific 1984.
Shang-keng Ma: Modern theory of critical phenomena. Addison-Wesley, Frontiers in Physics 1982.
N. Goldenfeld: Lectures on phase transitions and the renormalization group. Addison-Wesley, 1993.

Basierend auf einem Artikel in:

Wikipedia.de