Heteroübergang

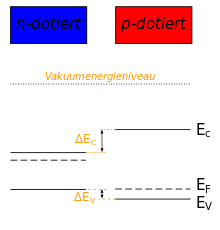
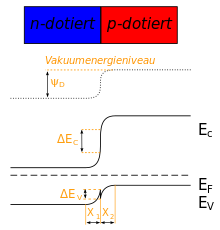
Bandenergien zweier Materialien unterschiedlicher Dotierung mit unterschiedlichem Bandabstand zwischen Valenzbandenergie E_v und Leitungsbandenergie E_c, ohne Kontakt.

Heteroübergang dieser Materialien mit Kontakt. Diffusionsspannung $\psi_D$ (siehe p-n-Übergang). Der Energieunterschied zum Vakuumenergieniveau entspricht der Ionisationsenergie.

Als Heteroübergang (auch Heterostruktur, engl. Heterojunction) wird die Grenzschicht zweier unterschiedlicher Halbleitermaterialien bezeichnet. Anders als bei einem p-n-Übergang ist hier nicht (nur) die Dotierungsart, sondern die Materialart verschieden. Die Halbleiter besitzen deshalb i. A. eine unterschiedliche Energie der Bandlücke und weisen besonderen elektrische und optische Eigenschaften auf.^[1]^[2]

Heteroübergänge werden meist aus III-V oder II-VI-Verbindungshalbleitern mittels Halbleiterepitaxie realisiert. Man spricht bei mehreren Schichten auch von Übergittern.

Der Nobelpreis für Physik 2000 wurde an Herbert Kroemer und Schores Iwanowitsch Alfjorow für Halbleiter-Heteroübergänge verliehen.^[3]^[4]^[5]

Berechnung

Bei einem p-n-Heteroübergang stellt sich eine Unregelmäßigkeit in den Energiebändern der Materialien ein. Die Ausdehnung dieser Unregelmäßigkeit, eine Verbiegung der Bandkanten, lässt sich über die Poissongleichung berechnen. Nimmt man den Übergang vom negativ dotierten Material 1 zum positiv dotierten Material 2 mit den relativen Dielektrizitätskonstanten $\varepsilon$ und Dotierungskonzentrationen $N_{{\mathrm {D}}}$ bzw. $N_{\mathrm {A} }$ an, stellt sich mit der Diffusionsspannung $\psi_\mathrm{D}$ bei angelegtem äußeren elektrischen Feld der Spannung eine Bandverbiegung der folgenden Größe ein:

$X_1 = \sqrt{\frac{2}{q}\frac{\varepsilon_1\varepsilon_2\cdot N_\mathrm{A}(\psi_\mathrm{D} - U)}{N_\mathrm{D}(\varepsilon_2 N_\mathrm{D}+\varepsilon_1 N_A)}}$ , $X_2 = \sqrt{\frac{2}{q}\frac{\varepsilon_1\varepsilon_2\cdot N_\mathrm{D}(\psi_\mathrm{D} - U)}{N_\mathrm{A}(\varepsilon_2 N_\mathrm{D}+\varepsilon_1 N_\mathrm{A})}}$

Anwendung

Laser & LEDs

Anwendung finden Heteroübergänge u.a. in Laserdioden: Wird bei optischer Rekombination Strahlung im Bereich mit der kleineren Bandlücke ausgesandt, kann diese nicht von Elektronen im Bereich der größeren Bandlücke absorbiert werden. Die Wahrscheinlichkeit, dass die Strahlung das Halbleitermaterial verlässt, ist also größer.

Mittels Doppelheterostrukturen gelang durch Durchbruch bei blauen und weißen Leuchtdioden. 2014 wurden die Forscher Isamu Akasaki, Hiroshi Amano und Shuji Nakamura mit dem Nobelpreis für Physik ausgezeichnet.^[6]^[7]

Solarzellen

Ein weiteres Anwendungsgebiet findet sich bei Solarzellen: Hier können unerwünschte Minoritätsladungsträger zu den Kontakten hin abgeschirmt werden, indem die höhere Bandlücke als Potential-Barriere für diese Ladungsträger genutzt wird. Auf diese Weise kann die Rekombination und somit der Verlust von Ladungsträgern am defektreichen Metall-Halbleiter-Kontakt und in den hochdotierten Schichten an den Kontakten reduziert werden, da den Majoritätsladungsträgern durch die Stufe im Heteroübergang die Rekombinationspartner in Form der Minoritätsladungsträger entzogen wurden. Mithilfe dieses Konzepts konnte 2014 ein Rekordwirkungsgrad von Siliciumsolarzellen von 25,6 % erreicht werden, indem amorphes Silicium als Material mit großer Bandlücke auf kristallinem Silicium verwendet wurde.^[8]

Die verschiedenen Solarzellentypen und jeweiligen Rekorde werden vom amerikanischen NREL getrackt.^[9]

Halbleiterbauelemente

Andere bekannte Bauteile sind z. B.,

High Electron Mobility Transistor (HEMT)
Heterojunction bipolar transistor (HBT).

Einzelnachweise

↑ Gerhard Abstreiter: Die Dimension macht den Unterschied. In: Physik Journal. Band 13, Nr. 8/9. Wiley-VCH, 2014 ( pro-physik.de).
↑ Tsuneya Ando, Alan B. Fowler, Frank Stern: Electronic properties of two-dimensional systems. In: Reviews of Modern Physics. Band 54, Nr. 2, 1. April 1982, ISSN 0034-6861, S. 437–672, doi: 10.1103/RevModPhys.54.437
↑ The Nobel Prize in Physics 2000.
↑ Herbert Kroemer: Nobel Lecture: Quasielectric fields and band offsets: teaching electrons new tricks. In: Reviews of Modern Physics. Band 73, Nr. 3, 22. Oktober 2001, ISSN 0034-6861, S. 783–793, doi: 10.1103/RevModPhys.73.783 (englisch, aps.org.
↑ Zhores I. Alferov: Nobel Lecture: The double heterostructure concept and its applications in physics, electronics, and technology. In: Reviews of Modern Physics. Band 73, Nr. 3, 22. Oktober 2001, ISSN 0034-6861, S. 767–782, doi: 10.1103/RevModPhys.73.767 (englisch, aps.org
↑ Shuji Nakamura: Nobel Lecture: Background story of the invention of efficient blue InGaN light emitting diodes. In: Reviews of Modern Physics. Band 87, Nr. 4, 5. Oktober 2015, ISSN 0034-6861, S. 1139–1151, doi: 10.1103/RevModPhys.87.1139 (englisch, aps.org
↑ The Nobel Prize in Physics 2014.
↑ Panasonic HIT® Solar Cell Achieves World's Highest Energy Conversion Efficiency*1 of 25.6%*2 at Research Level | Press Release. Panasonic Corporation, 10. April 2014,
↑ Best Research-Cell Efficiency Chart. National Renewable Energy Laboratory,

Basierend auf einem Artikel in:

Wikipedia.de