Keimbildung

Durch die Senkung des Umgebungsdrucks bilden sich Kohlendioxidblasen innerhalb eines kohlensäurehaltigen Erfrischungsgetränks.

Keimbildung oder Nukleation ist der erste Teilprozess, der einen Phasenübergang erster Ordnung einleitet. Beispiele hierfür sind das Gefrieren von Wasser zu Eis, Blasenbildung beim Übergang von der flüssigen zur gasförmigen Phase (z. B. beim Öffnen einer Wasserflasche mit gelöstem Kohlendioxid) oder die Kondensation eines Gases.

Allgemeines

Wesentliches Merkmal der Keimbildung ist, dass die neue, bei den gegebenen Bedingungen thermodynamisch stabile Phase, zunächst durch Keime aus der alten, metastabilen Phase gebildet wird.

Die Bildung dieser typischerweise nur nanometergroßen Keime ist zunächst kinetisch gehemmt. Flüssigkeiten lassen sich unterkühlen und überhitzen. Der Grund für diese Hemmung liegt in der Arbeit, die aufgebracht werden muss, um die gekrümmte Oberfläche eines kleinsten Keims (z.B. ein kugelförmiges Tröpfchen) der neuen Phase zu bilden. Für kleinste Tröpfchen oder Kristalle ist diese Oberflächenarbeit größer als der Energiegewinn aus dem Übergang in die neue, stabile Phase. Die daraus entstehende freie Energiebarriere nennt man Keimbildungsbarriere und die Arbeit, die aufgebracht werden muss, um diese Barriere zu überwinden, Keimbildungsarbeit (vgl. unten Thermodynamik). Der Bereich des Phasendiagramms, in dem die Keime unterhalb der kritischen Keimgröße bleiben, wird Ostwald-Miers-Bereich genannt.

Sind jedoch einmal Keime, die größer sind als die kritische Keimgröße, aus thermischen Fluktuationen gebildet, so wachsen sie schnell zur makroskopischen Phase an. Keimbildung kann damit auch als Prototyp eines aktivierten Prozesses verstanden werden.

Die Keimbildungsrate beschreibt, wie viele Keime der neuen Phase pro Volumen- und Zeiteinheit gebildet werden. Diese Keimbildungsrate hängt stark exponentiell von der Keimbildungsarbeit ab: je höher die Keimbildungsarbeit und damit die Barriere zur Keimbildung, desto niedriger die Rate (vgl. unten Kinetik).

Auftreten

Keimbildung ist ein allgegenwärtiger Prozess. So erfährt z.B. die von einem Vulkan ausgestoßene Lava einen schlagartigen Temperatur- und Drucksturz und bildet so die typischen, von kleinen Gasbläschen durchsetzten Gesteine. Ein anderes Beispiel sind Wetterphänomene wie die Bildung von Regen, Nebel und Schnee. In der Medizin kennt man z.B. die Taucherkrankheit, die durch zu schnelles Auftauchen verursacht wird; hier wird der zuvor im Blut gelöste Stickstoff durch den Druckabfall ausgegast.

Auch für die Industrie ist die Kenntnis der Keimbildungskinetik von höchstem Interesse, z.B. um den Tropfenschlag in Gasturbinen oder den Siedeverzug in Verdampfern zu verhindern oder um die Bildung des Kondensstreifens bei Düsenflugzeugen zu kontrollieren. Die Nukleation spielt darüber hinaus eine zentrale Rolle in der Verfahrenstechnik von Polymeren, Legierungen sowie manchen Keramiken, aber auch bei der Kontrolle bzw. Verhinderung der Kristallisation (z.B. bei Halbleitermaterialien, metallischen Gläsern oder Honig).

Electrofreezing ist ein Verfahren, durch das die Kristallisation von Wasser und anderen Flüssigkeiten beim Gefrierprozess gezielt durch das Anlegen eines elektrischen Feldes ausgelöst werden kann. Dieses physikalische Phänomen ist seit 1861 bekannt.

Klassische Keimbildungstheorie

Wegen ihrer großen technischen Relevanz werden Nukleationsprozesse seit dem Beginn des zwanzigsten Jahrhunderts systematisch untersucht. Substantielle Ergebnisse liegen bisher vor allem für den Phasenübergang gasförmig-flüssig, Kristallisation sowie für die Gefügeänderung in wenigen Metallen vor. Die hierfür aufgestellten Theorien werden mangels Alternative häufig auf die restlichen Systeme übertragen.

Bis heute herrscht aufgrund ihrer einfachen Struktur die klassische Keimbildungstheorie (classical nucleation theory) vor, obwohl insbesondere für den gasförmig-flüssig-Übergang wiederholt gezeigt wurde, dass ihre Vorhersagen typischerweise um mehrere Größenordnungen(!) von der Realität abweichen, z.B. bei Argon um mehr als 20 Größenordnungen. Solch große Abweichungen zwischen Theorie und Experiment sind nahezu einzigartig in der gegenwärtigen Naturwissenschaft. Dies ist umso erstaunlicher, als es sich im Wesentlichen um ein Problem der klassischen Physik handelt.

Die klassische Keimbildungstheorie macht einige grundlegende, vereinfachende Annahmen, die eine Beschreibung des Prozesses ermöglichen. Ein Großteil dieser Näherungen lässt sich unter dem Begriff ‚Kapillaritätsnäherung‘ zusammenfassen: Mit dieser Näherung wird angenommen, dass auch die kleinsten (mikroskopischen) Keime bereits die gleichen (makroskopischen) Eigenschaften der neuen Phase besitzen.

Zur Veranschaulichung der klassischen Keimbildungstheorie wird im Folgenden das Beispiel der Kondensation eines Tröpfchens aus einer übersättigten Gasphase verwendet. In diesem Fall wird der Prozess üblicherweise bei konstanter Temperatur betrachtet, und die treibende Kraft ist die Übersättigung.

Thermodynamik

Bei einer übersättigten Gasphase ist bei gegebener Temperatur der aktuelle Druck höher als der Gleichgewichtsdampfdruck $p_{\mathrm {eq} }(T)$ :

$p>p_{\mathrm {eq} }(T)\Leftrightarrow {\frac {p}{p_{\mathrm {eq} }(T)}}>1$

Die reversible Arbeit, die notwendig ist, um aus dieser übersättigten Gasphase ein flüssiges Tröpfchen zu formen, d.h. die Keimbildungsarbeit, lässt sich berechnen. Dazu wird ein Prozess bei konstantem Druck , konstantem Volumen und konstanter Teilchenzahl betrachtet. Das relevante thermodynamische Potential ist also die freie Gibbs-Energie:

$G=\mu N$

mit dem chemischen Potential $\mu$ .

Konkret für eine reine Dampfphase (Index v für engl. vapor) ergibt sich:

$G_\mathrm{v} = \mu_\mathrm{v} N$ .

Für ein System, das sowohl Dampf als auch ein flüssiges Tröpfchen (index l für engl. liquid) aus Teilchen enthält, ergibt sich:

$G(n)=\mu _{\mathrm {v} }(N-n)+\mu _{\mathrm {l} }n+\sigma A(n)$ ,

wobei $\sigma$ die Oberflächenspannung eines Tröpfchens mit der Oberfläche A(n) ist.

Die Keimbildungsarbeit für ein Tröpfchen der Größe in der Gasphase ist die Differenz $\Delta G(n)$ der freien Gibbs-Energie G(n) eines Systems, das ein Tröpfchen der Größe und Dampf enthält, und derjenigen des reinen Dampfsystems $G_{\mathrm {v} }=G(n=0)$ :

${\begin{alignedat}{2}\Delta G&=G(n)&&-G_{\mathrm {v} }\\&=-n\Delta \mu &&+\sigma A\end{alignedat}}$ .

In dieser Gleichung ist $\Delta \mu = \mu_\mathrm{v} - \mu_\mathrm{l}$ die Differenz der chemischen Potentiale des Dampfes und der Flüssigkeit.

Die klassische Keimbildungstheorie macht eine ganze Reihe vereinfachender Annahmen:

Das flüssige Tröpfchen ist kugelförmig, inkompressibel und hat eine scharfe Grenzfläche.
Das flüssige Tröpfchen hat die gleiche Oberflächenspannung, Dichte und Dampfdruck wie die makroskopische (flache) flüssige Phase.
Der Dampfdruck kann mit Hilfe des idealen Gasgesetzes beschrieben werden.

Mit Hilfe dieser Annahmen und der Gibbs-Duhem-Gleichung lässt sich die Differenz der chemischen Potentiale berechnen:

${\begin{aligned}\Delta \mu &=k_{\mathrm {B} }T\ln \left({\frac {p}{p_{\mathrm {eq} }(T)}}\right)\\&=k_{\mathrm {B} }T\ln {S}\end{aligned}}$ .

mit

der Boltzmann-Konstanten $k_{\mathrm {B} }$
der Übersättigung $S=p/p_{\mathrm {eq} }(T)>1$ .

Auch die Oberfläche lässt sich berechnen:

$A(n)=4\pi r^{2}(n)=s_{1}n^{2/3}$

mit

dem Radius des Tröpfchens
dem mittleren Oberflächenbedarf eines Teilchens (Moleküls)
- dem mittleren Volumen $v_\mathrm{l}$ eines Teilchens in der flüssigen Phase.

Damit ergibt sich für die Keimbildungsarbeit

$\Delta G = -n k_\mathrm{B} T \ln S + \sigma s_1 n^{2/3}$ .

Der erste Term, auch Volumenterm genannt, ist proportional zu . Er stellt den Gewinn (daher negatives Vorzeichen) an Energie dar, der beim Übergang eines Moleküls aus der metastabilen Dampfphase in die stabile flüssige Phase auftritt.

Der zweite Term ist die Arbeit, die aufgebracht werden muss (daher positives Vorzeichen), um die Oberfläche eines solchen flüssigen Tröpfchens zu formen. Er ist proportional zu $n^{2/3}$ .

Bei S>1 – nur für diesen Fall kann Keimbildung einsetzen – dominiert der Oberflächenterm für kleine Teilchenzahlen bzw. Tröpfchengrößen. Ab einer kritischen Tröpfchengröße $n^{{*}}$ gewinnt der Volumenterm Oberhand. Das Maximum $\Delta G^{*}$ ist die Keimbildungsarbeit, die aufgebracht werden muss, um ein Tröpfchen der kritischen Größe zu bilden. Dies ergibt das gezeigte Bild einer Barriere in der freien Energie $\Delta G(n)$ .

Klassische Keimbildungstheorie: Keimbildungsarbeit als Funktion der Tröpfchengröße; rote Linie: Beitrag des Oberflächenterms, grüne Linie: ... des Volumenterms

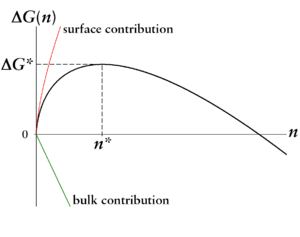
Die kritische Größe und die kritische Keimbildungsarbeit sind die bestimmenden Größen der Keimbildung:

Tröpfchen kleiner als $n^{{*}}$ haben eine höhere Wahrscheinlichkeit, wieder zu verdampfen als weiter zu wachsen, da für sie das Verdampfen mit einem Gewinn an freier Gibbs-Energie verbunden ist (Bewegung nach unten auf der Kurve).
Nur Tröpfchen größer als $n^{{*}}$ haben eine höhere Wahrscheinlichkeit, weiter zu wachsen als zu verdampfen, und können damit als Keime der neuen Phase dienen.

Damit ist verständlich, warum eine Substanz für längere Zeit metastabil gehalten werden kann: Obwohl die neue Phase (in unserem Beispiel die flüssige) die thermodynamisch stabile Phase ist, muss der Prozess zunächst einige energetisch ungünstige Schritte durchlaufen, um die Barriere zu erklimmen.

Die Barriere und die kritische Keimgröße nach der klassischen Keimbildungstheorie sind:

$\Delta G^{*} = \frac{16\pi}{3}\frac{v_{l}^{2}\sigma^{3}}{(k_\mathrm{B}T\ln S)^{2}}$

und

$n^{*}=2\Delta G^{*}/k_{\mathrm {B} }T\ln S$ .

Kinetik

Um nun eine Keimbildungsrate zu berechnen, also die Anzahl der pro Volumen und Zeit gebildeten Keime, muss auch die Kinetik der Keimbildung betrachtet werden. Die stationäre Keimbildungsrate wird üblicherweise in Form eines Arrhenius-Ansatzes berechnet:

$J=Ke^{-\Delta G^{*}/k_{\mathrm {B} }T}$

Der Vorfaktor wird üblicherweise der kinetische Vorfaktor genannt, auf ihn wird hier jedoch nicht näher eingegangen. Üblicherweise hat die Höhe $\Delta G^{*}$ der Barriere aufgrund der exponentiellen Abhängigkeit einen wesentlich größeren und entscheidenden Einfluss.

Arten der Keimbildung

Homogene Keimbildung

Erfolgt die Nukleation im freien Raum, also durch ein statisches Zusammentreffen gleicher Teilchen, so spricht man von einer homogenen Keimbildung.

Hierzu ist es notwendig, dass sich im Falle der Kondensation ausreichend viele und langsame Teilchen ohne weitere Hilfe zu größeren Strukturen zusammenfinden. Langsame Teilchen können durch das gleichzeitige Zusammentreffen von mehr als zwei Teilchen (Dreierstoß) entstehen. Hierbei nimmt ein Teilchen einen Großteil der kinetischen Energie auf und hinterlässt zwei langsame Teilchen. Die Übersättigung ist dabei ungefähr proportional zur Wahrscheinlichkeit eines derartigen Dreierstoßes, der zur Nukleation führt. Abhängig von dem betrachteten System können daher thermodynamisch metastabile Systeme sehr lange in diesem Zustand verharren.

Heterogene Keimbildung

Im Gegensatz zur homogenen Keimbildung benötigt man bei der heterogenen Keimbildung nur sehr geringe Übersättigungen von oft unter einem Prozent. Diese Form der Kondensation erfolgt im Fall der Kondensation an bereits existierenden Oberflächen (heterogen: an andersartigen Teilchen), also im Regelfall an festen Partikeln, die in der Gasphase schweben, den Kondensationskernen bzw. Aerosolteilchen. Diese fungieren in Bezug auf das jeweilige Gas als eine Art Teilchenfänger, wobei im Wesentlichen der Radius und die chemischen Eigenschaften des Partikels bestimmen, wie gut die Gasteilchen an ihm haften. Analog gilt dies auch für Oberflächen nicht partikulärer Körper, wobei man dann von einem Beschlag spricht. In jedem Falle wirken heterogene Teilchen oder Oberflächen als ein Katalysator für die Keimbildung, indem sie die Keimbildungsbarriere deutlich verringern.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de