Arrhenius-Gleichung
Die Arrhenius-Gleichung, benannt nach Svante Arrhenius, beschreibt näherungsweise eine quantitative Temperaturabhängigkeit bei physikalischen und vor allem chemischen Prozessen, bei denen auf molekularer Ebene eine Aktivierungsenergie überwunden werden muss. Die Arrhenius-Gleichung beschreibt eine phänomenologische Beziehung und gilt für sehr viele chemische Reaktionen. Die Arrhenius-Gleichung ist mit der Eyring-Gleichung verwandt, die einen Zusammenhang der mikroskopischen Deutung darstellt.
Arrhenius-Gleichung in der chemischen Reaktionskinetik
Die Arrhenius-Gleichung beschreibt in der chemischen
Kinetik für den Spezialfall monomolekularer Reaktionen die quantitative
Abhängigkeit der Reaktionsgeschwindigkeitskonstanten
von der Temperatur:
mit
präexponentieller oder Frequenzfaktor, entspricht nach der Stoßtheorie dem Produkt aus der Stoßzahl Z und dem Orientierungsfaktor P:
Aktivierungsenergie (Einheit: J·mol−1),
universelle Gaskonstante (8,314 J·K−1·mol−1),
absolute (thermodynamische) Temperatur (Einheit: K).
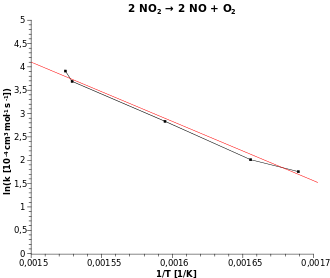
Der Arrheniusgraph ist eine graphische Darstellung, bei der die logarithmierte Geschwindigkeitskonstante gegen den Kehrwert der Temperatur aufgetragen wird (vgl. Abb.):
Temperaturabhängigkeit des Frequenzfaktors
Die Arrhenius-Gleichung gilt jedoch nicht exakt, weil auch
temperaturabhängig ist und häufig der Gesetzmäßigkeit
folgt. Somit nimmt auch der präexponentielle Faktor mit steigender Temperatur in geringem Maß (Wurzelfunktion) zu. Seine Temperaturabhängigkeit ist jedoch deutlich geringer als die des Exponentialterms. In diesem Fall kann eine modifizierte Arrhenius-Gleichung verwendet werden:
Mit dem zur Arrhenius-Zahl
zusammengefassten Exponenten
wird die Arrhenius-Gleichung auch dimensionslos dargestellt:
Arrhenius-Gleichung bei anderen Prozessen
Die Temperaturabhängigkeit der Viskosität von Flüssigkeiten sowie der Diffusionskoeffizienten in Feststoffen wird ebenfalls durch eine Arrhenius-Gleichung beschrieben.
Berechnung der Aktivierungsenergie
Durch Messen zweier Geschwindigkeitskonstanten ,
und zweier Temperaturen
derselben Reaktion kann die Aktivierungsenergie durch das Aufstellen der
Arrhenius-Gleichung für die beiden Messungen wie folgt berechnet werden:
Ziehen des Natürlichen Logarithmus:
Subtraktion der Gleichungen (2') − (1') liefert:
Durch die Subtraktion entfällt
und das Vorzeichen im 2. Term wechselt:
Zusammenfassen des natürlichen Logarithmus und Ausklammern liefert:
Umstellen nach :
multiplizieren mit
und dividieren durch
ergibt schließlich
Vervielfachung der Reaktionsgeschwindigkeit und Aktivierungsenergie
Temperaturerhöhung führt zur Zunahme der Reaktionsgeschwindigkeit. Eine
Faustregel, die sogenannte Reaktionsgeschwindigkeit-Temperaturregel
(RGT-Regel), sagt bei einer Temperaturerhöhung von
eine Verdopplung bis Vervierfachung der Reaktionsgeschwindigkeit voraus. Der
Faktor, um den sich die Reaktionsgeschwindigkeit bei einer Temperaturerhöhung
von 10 K ändert, wird als Q10-Wert bezeichnet.
Nimmt man bei Anstieg der Temperatur von
auf
eine Verdopplung der Reaktionsgeschwindigkeit an, so gilt
.
Vorausgesetzt,
ist temperaturunabhängig, folgt daraus:
Durch Logarithmieren erhält man
und durch Ausformulieren des Quotienten im Logarithmus:
Vereinfachen der rechten Seite ergibt:
Ausklammern führt zu:
und Umstellen nach
ergibt:
Die 2 im Logarithmus entspricht einer Verdopplung der Reaktionsgeschwindigkeit, die hiernach bei einer bestimmten Temperatur und Temperaturdifferenz auch nur für eine bestimmte Aktivierungsenergie stattfindet. Die RGT-Regel ist also nur eine grobe Näherung.
Für eine Ver--fachung
der Reaktionsgeschwindigkeit gilt analog:
und somit:
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.03. 2024