Fehlerrechnung
Es ist praktisch nie möglich, exakt zu messen. Die Abweichungen der Messwerte von ihren wahren Werten wirken sich auf ein Messergebnis aus, so dass dieses ebenfalls von seinem wahren Wert abweicht. Die Fehlerrechnung versucht, die Einflussnahme der Messabweichungen auf das Messergebnis quantitativ zu bestimmen.
Messabweichungen wurden früher als Messfehler bezeichnet. Der Begriff Fehlerrechnung ist noch ein Überbleibsel aus jener Zeit.
Abgrenzung
Der Begriff Fehlerrechnung kann verschieden verstanden werden.
- Häufig will man ein Messergebnis
aus einer Messgröße
oder im allgemeinen Fall aus mehreren Messgrößen
mittels einer bekannten Gleichung (mathematische Formel) berechnen. Bei fehlerhafter Bestimmung der Eingangsgröße(n) wird auch die Ausgangsgröße falsch bestimmt, denn die Einzelabweichungen werden mit der Gleichung
bzw.
übertragen und führen zu einer Abweichung des Ergebnisses. Man nennt dieses Fehlerfortpflanzung. Unter diesem Stichwort werden Formeln angegeben getrennt für die Fälle, dass die Abweichungen (im Sprachgebrauch teilweise noch als Fehler bezeichnet) bekannt sind als
-
- systematische Abweichungen (systematische Fehler),
- Fehlergrenzen oder
- Unsicherheiten infolge zufälliger Abweichungen (zufälliger Fehler).
- Kennzeichnend ist hier: Man hat im allgemeinen Fall mehrere Größen
und zu jeder Größe einen Messwert.
- Wenn man die Messung einer Größe
unter gleichen Bedingungen wiederholt, stellt man häufig fest, dass sich die Einzelmesswerte unterscheiden; sie streuen. Sie haben dann
-
- zufällige Abweichungen (zufällige Fehler).
- Nachfolgend werden Formeln angegeben zur Berechnung eines von diesen Abweichungen möglichst befreiten Wertes und zu dessen verbleibender Messunsicherheit.
- Kennzeichnend ist hier: Man hat zu einer Größe
mehrere Messwerte.
Normalverteilung
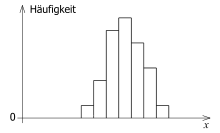
Die Streuung von Messwerten kann man sich in einem Diagramm veranschaulichen.
Man teilt den Bereich der möglichen Werte in kleine Bereiche mit der Breite
ein und trägt zu jedem Bereich auf, wie viele gemessene Werte in diesem Bereich
vorkommen, siehe Beispiel in nebenstehendem Bild.
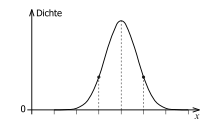
Bei der Gauß– oder Normalverteilung
(nach Carl
Friedrich Gauß) lässt man die Anzahl der Messungen
gehen und zugleich
.
Bei dem Diagramm geht der gestufte Verlauf über in eine stetige Kurve. Diese
beschreibt
- die Dichte der Messwerte in Abhängigkeit vom gemessenen Wert und außerdem
- für eine zukünftige Messung, welcher Wert mit welcher Wahrscheinlichkeit zu erwarten ist.
Mit der mathematischen Darstellung der Normalverteilung lassen sich viele statistisch bedingte natur-, wirtschafts- oder ingenieurwissenschaftliche Vorgänge beschreiben. Auch zufällige Messabweichungen können in ihrer Gesamtheit durch die Parameter der Normalverteilung beschrieben werden. Diese Kenngrößen sind
- der arithmetische Mittelwert über alle Messwerte, genannt Erwartungswert. Dieser ist so groß wie die Abszisse des Maximums der Kurve. Zugleich liegt er an der Stelle des wahren Wertes.
- die Standardabweichung als Maß für die Breite der Streuung der Messwerte. Sie ist so groß wie der horizontale Abstand eines Wendepunktes vom Maximum. Im Bereich zwischen den Wendepunkten liegen etwa 68 % aller Messwerte.
Unsicherheit einer einzelnen Messgröße
Das Folgende gilt bei Abwesenheit von systematischen Abweichungen und bei normalverteilten zufälligen Abweichungen.
Schätzwerte der Parameter
Hat man von der Größe
mehrere mit zufälligen Fehlern behaftete Werte
mit
,
so kommt man gegenüber dem Einzelwert zu einer verbesserten Aussage durch
Bildung des arithmetischen Mittelwertes
.
Die (empirische) Standardabweichung
ergibt sich aus
.
Diese Größen sind Schätzwerte für die Parameter der Normalverteilung. Durch
die endliche Zahl der Messwerte unterliegt auch der Mittelwert noch zufälligen
Abweichungen. Ein Maß für die Breite der Streuung des Mittelwertes ist die
Unsicherheit
.
Diese wird umso kleiner, je größer
wird. Sie kennzeichnet zusammen mit dem Mittelwert einen Wertebereich
,
in dem der wahre Wert der Messgröße erwartet wird.
Vertrauensniveau
Diese Erwartung wird nur mit einer gewissen Wahrscheinlichkeit erfüllt. Will
man Letztere auf ein konkretes Vertrauensniveau festlegen, so muss man einen
Bereich (ein Konfidenzintervall)
festlegen, in dem der wahre Wert mit dieser Wahrscheinlichkeit liegt. Je höher
die Wahrscheinlichkeit gewählt wird, desto breiter muss der Bereich sein. Der
Faktor
berücksichtigt das gewählte Vertrauensniveau und die Anzahl der Messungen
insoweit, als mit einer kleinen Zahl
die statistische Behandlung noch nicht aussagekräftig ist. Wählt man die oben
genannte Zahl 68 % als Vertrauensniveau und
,
so ist
.
Für das in der Technik vielfach verwendete Vertrauensniveau von 95 % und
für
ist
.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.03. 2022