Poincaré-Abbildung

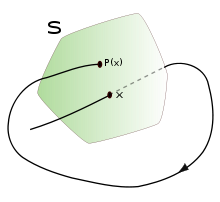
Illustration der Wiederkehr einer Trajektorie nach .

Die Poincaré-Abbildung (auch Poincaré map, first return map, nach dem französischen Mathematiker Henri Poincaré) ist eine mathematische Methode zur Untersuchung des Flusses eines kontinuierlichen n-dimensionalen dynamischen Systems. Dazu betrachtet man die Schnittpunkte einer Trajektorie mit einer (n-1)-dimensionalen transversalen Hyperfläche $\Sigma$ , dem Poincaré-Schnitt. Die Poincaré-Abbildung ist die Abbildung die jedem dieser Schnittpunkte den jeweils nächsten P(x) zuordnet und ist somit ein (n-1)-dimensionales diskretes dynamisches System.

Beispiel

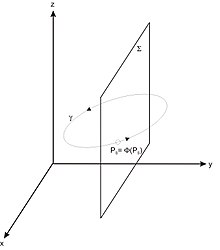
Poincaré-Schnitt für eine periodische Trajektorie $\gamma$

Betrachte die Differentialgleichung ${\dot {x}}(t)=f(x(t))$ und bezeichne mit $\Phi (t,x)$ den Fluss, also die Lösung zur Anfangsbedingung $\Phi (0,x)=x$ . Angenommen, es gibt eine periodische Trajektorie, also eine Lösung $\Phi (t,p)$ , die bei startet und nach einer bestimmten Zeit $\tau$ wieder dorthin zurückkehrt, $\Phi (\tau ,p)=p$ . Dann kann man eine Fläche $\Sigma$ wählen, die transversal zur Trajektorie $\Phi (t,p)$ ist und diese in schneidet. Alle Trajektorien, die in Punkten $x\in \Sigma$ in der Nähe von starten, werden dann nach einer bestimmten Zeit wieder die Fläche schneiden. Es gibt also eine kleinste positive Zeit $\tau (x)>0$ , für die $\Phi (\tau (x),x)\in \Sigma$ gilt. Dann ist die Poincaré-Abbildung gegeben durch $P(x)=\Phi (\tau (x),x)$ . Speziell für die periodische Trajektorie erhält man einen Fixpunkt: P(p)=p . Die Frage, ob die periodische Trajektorie stabil ist, ist nun äquivalent zur Frage, ob der entsprechende Fixpunkt der Poincaré-Abbildung stabil ist.

Anwendung

Die Poincaré-Abbildung ist besonders zur Untersuchung der geometrischen Strukturen chaotischer Attraktoren geeignet, da die zeitliche Diskretisierung eine wesentliche Vereinfachung darstellt.

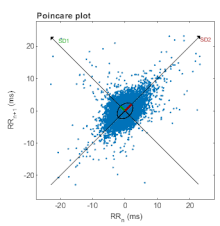
In der Kardiologie findet die Darstellung bei der Auswertung eines Langzeit-EKGs Verwendung. Durch Anwendung auf die Abstände zwischen den jeweiligen Herzschlägen kann auf Herzrhythmusstörungen wie Vorhofflimmern rückgeschlossen werden.

Eine weitere Anwendung findet sich in der Stressforschung: hier lassen sich aus den Poincaré-Abbildungen mit den beiden orthogonal aufeinander stehenden Durchmessern SD1 und SD2 die parasympathischen und sympathischen Einflüsse auf die Herzfrequenz ablesen (Herzfrequenzvariabilität).

Literatur

Herbert Amann: Gewöhnliche Differentialgleichungen. 2. Auflage. de Gruyter, Berlin 1995, ISBN 3-11-014582-0.>

Basierend auf einem Artikel in:

Wikipedia.de