
Quadratsummen-Funktion
Die Quadratsummen-Funktion (engl. sum of squares function) ist
eine zahlentheoretische
Funktion, die angibt, auf wie viele Arten eine gegebene natürliche Zahl
als Summe von
Quadraten ganzer Zahlen dargestellt werden kann, wobei alle Vertauschungen
und Vorzeichenkombinationen mitgezählt werden. Sie wird bezeichnet als
.
Definition
| n | n | r1(n) | r2(n) | r3(n) | r4(n) | r5(n) | r6(n) | r7(n) | r8(n) |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| 2 | 2 | 0 | 4 | 12 | 24 | 40 | 60 | 84 | 112 |
| 3 | 3 | 0 | 0 | 8 | 32 | 80 | 160 | 280 | 448 |
| 4 | 22 | 2 | 4 | 6 | 24 | 90 | 252 | 574 | 1136 |
| 5 | 5 | 0 | 8 | 24 | 48 | 112 | 312 | 840 | 2016 |
| 6 | 2‧3 | 0 | 0 | 24 | 96 | 240 | 544 | 1288 | 3136 |
| 7 | 7 | 0 | 0 | 0 | 64 | 320 | 960 | 2368 | 5504 |
| 8 | 23 | 0 | 4 | 12 | 24 | 200 | 1020 | 3444 | 9328 |
| 9 | 32 | 2 | 4 | 30 | 104 | 250 | 876 | 3542 | 12112 |
| 10 | 2‧5 | 0 | 8 | 24 | 144 | 560 | 1560 | 4424 | 14112 |
| 11 | 11 | 0 | 0 | 24 | 96 | 560 | 2400 | 7560 | 21312 |
| 12 | 22‧3 | 0 | 0 | 8 | 96 | 400 | 2080 | 9240 | 31808 |
| 13 | 13 | 0 | 8 | 24 | 112 | 560 | 2040 | 8456 | 35168 |
| 14 | 2‧7 | 0 | 0 | 48 | 192 | 800 | 3264 | 11088 | 38528 |
| 15 | 3‧5 | 0 | 0 | 0 | 192 | 960 | 4160 | 16576 | 56448 |
| 16 | 24 | 2 | 4 | 6 | 24 | 730 | 4092 | 18494 | 74864 |
| 17 | 17 | 0 | 8 | 48 | 144 | 480 | 3480 | 17808 | 78624 |
| 18 | 2‧32 | 0 | 4 | 36 | 312 | 1240 | 4380 | 19740 | 84784 |
| 19 | 19 | 0 | 0 | 24 | 160 | 1520 | 7200 | 27720 | 109760 |
| 20 | 22‧5 | 0 | 8 | 24 | 144 | 752 | 6552 | 34440 | 143136 |
Die Funktion ist definiert als
,
d.h. als Anzahl der Darstellungsmöglichkeiten von
als Summe von
Quadraten ganzer Zahlen mit
. Es
sei
.
Beispielsweise ist ,
da
mit jeweils 2 Vorzeichenkombinationen gilt, und auch
wegen
mit 4 Vorzeichenkombinationen. Andererseits ist
,
weil es keine Darstellung der Zahl 3 als Summe von 2 Quadraten gibt.
Aus der Definition folgt sofort die Beziehung
aus der sich eine Rekursionsformel zur effizienten Berechnung ableiten lässt:
Durchschnittliche Größenordnung
Es sei
.
Das ist anschaulich die Anzahl der (ganzzahligen) Gitterpunkte in einer -dimensionalen
Kugel mit dem Radius
und darum näherungsweise gleich dem Kugelvolumen. Genauer lässt sich rekursiv
ableiten
,
wobei die Konstanten
die Volumina der
-dimensionalen
Einheitskugeln sind:
und
das Landau-Symbol
ist.
Die durchschnittliche
Größenordnung von
ist damit
,
also z.B.
die von
.
Erzeugende Funktion
Die erzeugende
Funktion erhält man als Potenz der Jacobischen
Thetafunktion
für den Spezialfall
.
Dafür gilt
Man erhält daraus
Spezielle Fälle


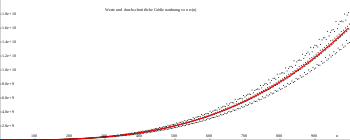
Einfache Formeln ergeben sich für gerades ,
z.B. (
):
Für
gilt:
Mit Hilfe der Primfaktorzerlegung ,
wobei
die Primfaktoren der Form
und
die Primfaktoren der Form
sind, ergibt sich als weitere Formel
,
wenn alle Exponenten
gerade sind. Ist mindestens ein
ungerade, dann ist
.
Nach Definition ist
auch die Anzahl aller Gaußschen
Zahlen mit der Norm
.
Die Formel für
stammt von Carl Gustav Jacob Jacobi und ist gegeben als achtfache Summe aller Teiler von
die nicht durch 4 teilbar sind (Satz
von Jacobi):
ist auch die Anzahl aller Lipschitz-Quaternionen
mit der Norm
.
Jacobi fand auch eine explizite Formel für :
Beziehung zur Sierpiński-Konstanten
Der Limes
existiert und wird (nach Wacław Sierpiński) als Sierpiński-Konstante bezeichnet. Diese lässt sich durch die Kreiszahl, die Euler-Mascheroni-Konstante und die Gammafunktion ausdrücken:
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 23.08. 2022