Diskrete Kosinustransformation

Die diskrete Kosinustransformation (englisch discrete cosine transformation, DCT) ist eine Transformation der numerischen Mathematik. Sie wird z.B. für die verlustbehaftete Kompression von Audio- und Bilddaten verwendet. Für Bilddaten wird sie beispielsweise beim Kompressionsverfahren JPEG verwendet, im Bereich der Audiodatenkompression findet eine modifizierte diskrete Kosinustransformation (MDCT) Anwendung, beispielsweise im Rahmen des AAC-Formats. Die diskrete Kosinustransformation wurde 1974 von Nasir Ahmed, T. Natarajan und K. R. Rao erstmals beschrieben.

Zusammenhang

Die diskrete Kosinustransformation zählt zu den reellwertigen, diskreten, linearen, orthogonalen Transformationen, die ähnlich der diskreten Fouriertransformation (DFT) ein zeitdiskretes Signal von dem Zeitbereich (bei Zeitsignalen) oder dem Ortsbereich (bei räumlichen Signalen) in den Frequenzbereich transformiert.

Audio- und Videosignale weisen typischerweise im unteren Spektralbereich hohe Signalenergien auf, zu deren Dekorrelation sich die DCT besonders gut eignet und die verbreitete Verwendung dieser Transformation erklärt. Weitere untergeordnete Anwendungen liegen bei der Lösung von partiellen Differentialgleichungen mittels spektraler Lösungsmethoden. Die DCT besitzt im Rahmen der Tschebyschow-Approximation mathematischen Bezug zu den Tschebyschow-Polynomen. Sie ist weiterhin eng verwandt mit der diskreten Sinustransformation (DST).

Beschreibung

Wie andere diskrete Frequenztransformationen drückt auch die diskrete Kosinustransformation eine endliche Eingangssignalfolge als eine endliche Summe von gewichteten trigonometrischen Funktionen mit unterschiedlichen Frequenzen aus. Bei der Kosinustransformation finden nur Kosinusfunktionen Anwendung.

Die diskrete Fouriertransformation, welche über eine endliche Eingangsfolge definiert ist, besitzt implizit durch die Art der Transformation und deren Randbedingungen auch eine Festlegung, wie die Eingangsdatenfolge außerhalb dieser endlichen Folge fortgesetzt wird. Im Fall der diskreten Fouriertransformation ist dies eine periodische Fortsetzung, im Fall der diskreten Kosinustransformation ist dies eine gerade Fortsetzung der erzeugenden Signalfolge.

Bei der Art der Fortsetzung der Eingangsdatenfolge und deren Unterscheidung in gerade und ungerade Fortsetzung ergeben sich unterschiedliche Kombinationen. Es bestehen zwei Randbereiche der Eingangsfolge (Anfang und Ende der Folge), welche jeweils gerade oder ungerade fortgesetzt werden können. Daraus ergeben sich vier verschiedene Möglichkeiten. Weiter ist festzulegen, ab welcher Position in der Folge die Fortsetzung zu erfolgen hat. Dabei kann die Fortsetzung genau am Wert erfolgen oder zwischen zwei Werten. Falls die Fortsetzung zwischen zwei Werten liegt, wird der erste und der letzte Wert der Folge dupliziert. Diese Festlegung erfolgt getrennt nach Anfang und Ende der Folge, womit sich wieder vier verschiedene Kombinationen ergeben. So ergeben sich $4\cdot 4=16$ verschiedene Formen der Fortsetzung, d.h. mögliche Formen der Randwerte.

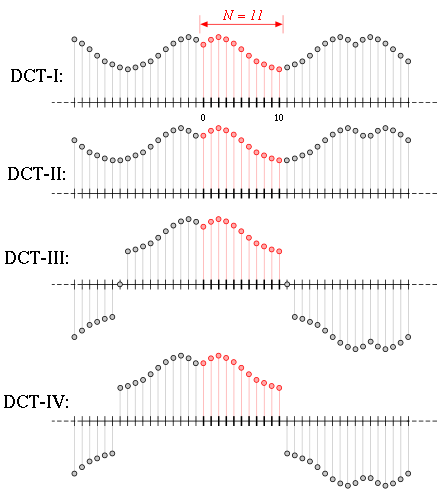
Darstellung der impliziten Fortsetzung am Beispiel einer Eingangsdatenfolge mit 11 Werten (in rot) und deren Möglichkeiten zur geraden und ungeraden Fortsetzungen im Rahmen der vier üblichen DCT-Varianten (DCT Typ I bis IV)

Die acht Randwertbedingungen bei der Fortsetzung, die am Anfang einer Folge eine gerade Fortsetzung aufweisen, werden zu der diskreten Kosinustransformation gezählt, die restlichen acht Formen mit einer ungeraden Fortsetzung am Anfang der Folge ergeben die diskrete Sinustransformation (DST). Die verschiedenen Formen werden in der Literatur als DCT-I bis DCT-VIII und DST-I bis DST-VIII bezeichnet. Die vier im Bereich der Datenkompression wesentlichen Varianten DCT-I bis DCT-IV und deren Fortsetzungen sind in nebenstehender Abbildung dargestellt. Die anderen vier Varianten der DCT und alle 8 Varianten der DST besitzen im Bereich der Datenkompression keine Bedeutung.

Diese unterschiedlich fortgesetzten Folgen bestimmen wesentlich die Eigenschaft der einzelnen Transformationen und deren praktische Bedeutung. Bei der Lösung von partiellen Differentialgleichungen mittels Spektraltransformation werden dabei je nach Problemstellung alle Varianten der DCT oder DST eingesetzt. Im Bereich der verlustbehafteten Datenreduktion von Bildsignalen wie bei JPEG findet die DCT-II in einer zweidimensionalen Transformation Anwendung, weshalb umgangssprachlich unter der „DCT“ oder der FDCT für forward discrete cosine transform der Typ DCT-II verstanden wird. Die Umkehrung der DCT-II ist aus Symmetriegründen und bis auf einen konstanten Faktor die DCT-III, auch als IDCT für inverse discrete cosine transform (dt. inverse diskrete Kosinustransformation) bezeichnet. Im Bereich der verlustbehafteten Audiosignalkompression, wie dem Dateiformat MP3, muss ein fortlaufender diskreter Audiodatenstrom transformiert werden, wobei zur Vermeidung von Alias-Effekten im Zeitbereich die MDCT, die auf einer eindimensionalen DCT-IV basiert, eingesetzt wird.

Im Bereich der Bild- und Audiokompression bestimmt die Art der Fortsetzung und somit die Randwerte, wie gut sich die Transformation für die Datenkompression eignet. Der Grund dafür ist, dass Sprünge in der Signalfolge zu hohen Koeffizientenwerten in allen Frequenzbändern und damit insbesondere zu hochfrequenten spektralen Anteilen führen. Dies gilt auch, wenn diese Sprünge an den Rändern der Signalfolge infolge einer ungünstigen Fortsetzung auftreten.

Die diskrete Fouriertransformation ist im Allgemeinen eine komplexwertige Transformation und durch die periodische Fortsetzung können an den Randstellen Sprünge im Signalverlauf auftreten. Dies gilt auch für die diskrete Sinustransformation, die am Anfang der Folge eine ungerade Fortsetzung aufweist.

Im Gegensatz zur diskreten Fourier-Transformation sind alle Formen der DCT reelle Transformationen und liefern reelle Koeffizienten.

Die DCT transformiert, aufgrund der Wahl der Art der Fortsetzung an den Rändern, Signale (z.B. Bild- oder Audiosignale) in ihre spektralen Komponenten.
Die DCT kann sowohl in Software als auch in Hardware effizient implementiert werden. Es existieren ähnliche Implementierungen wie bei der schnellen Fourier-Transformation (FFT). Unter Verwendung von Signalprozessoren und deren Multiply-Accumulate-Befehlen (MAC) lässt sich die DCT-Berechnung effizient realisieren.

Definition

Die verschiedenen Arten der DCT bilden jeweils die reellwertige Eingabefolge (Orts- oder Zeitbereich) mit Elementen x[n] auf eine reellwertige Ausgabefolge (Spektralbereich) $X[n]$ ab:

$x[n]=x_{0},\ldots ,x_{{N-1}}\Rightarrow X[n]=X_{0},\ldots ,X_{{N-1}}$

DCT-I

Die DCT-I ist bezüglich ihrer Randwerte gerade am Anfang um $x_{0}$ und gerade am Ende um $x_{N-1}$ .

$X_{k}={\frac {1}{2}}(x_{0}+(-1)^{k}x_{{N-1}})+\sum _{{n=1}}^{{N-2}}x_{n}\cos \left[{\frac {\pi }{N-1}}nk\right]\quad \quad k=0,\dots ,N-1$

Die DCT-I entspricht, bis auf einen Faktor von 2, der DFT einer reellen Folge der Länge $2N-2$ mit gerader Symmetrie. Beispielsweise ist die DCT-I einer $N=5$ Zahlen langen Folge abcde bis auf den Faktor 2 identisch zu der DFT der Folge abcdedcb. Die DCT-I ist nur für Folgen mit minimaler Länge von 2 definiert, für alle anderen DCT-Varianten muss ganzzahlig positiv sein.

DCT-II

Die DCT-II ist die übliche DCT. Sie ist bezüglich ihrer Randwerte gerade am Anfang um $x_{-1/2}$ und gerade am Ende um $x_{N-1/2}$ .

$X_{k}=\sum _{{n=0}}^{{N-1}}x_{n}\cos \left[{\frac {\pi }{N}}\left(n+{\frac {1}{2}}\right)k\right]\quad \quad k=0,\dots ,N-1$

Die DCT-II entspricht bis auf den konstanten Faktor 2 der DFT einer reellen Folge von $4N$ Elementen mit gerader Symmetrie, wobei alle Elemente mit geradem Index den Wert 0 aufweisen.

DCT-III

Die DCT-III ist die Umkehrung der DCT-II. Sie ist bezüglich ihrer Randwerte gerade am Anfang um $x_{0}$ und ungerade am Ende um $x_{N}$ . Die Ausgabefolge ist gerade am Anfang um $X_{-1/2}$ und gerade am Ende um $X_{N-1/2}$ .

$X_{k}={\frac {1}{2}}x_{0}+\sum _{{n=1}}^{{N-1}}x_{n}\cos \left[{\frac {\pi }{N}}n\left(k+{\frac {1}{2}}\right)\right]\quad \quad k=0,\dots ,N-1$

DCT-IV

Die DCT-IV ist bezüglich ihrer Randwerte gerade am Anfang um $x_{-1/2}$ und ungerade am Ende um $x_{N-1/2}$ .

$X_{k}=\sum _{{n=0}}^{{N-1}}x_{n}\cos \left[{\frac {\pi }{N}}\left(n+{\frac {1}{2}}\right)\left(k+{\frac {1}{2}}\right)\right]\quad \quad k=0,\dots ,N-1.$

Eine Variante der DCT-IV ist die modifizierte diskrete Kosinustransformation (MDCT), wobei dabei die Datenfolgen der einzelnen Datenblöcke ähnlich wie bei dem Overlap-Add-Verfahren überlappt werden, um einen aperiodischen Verlauf zu erhalten.

Umkehrung

Wie einige andere Transformationen kann auch die DCT umgekehrt werden. Die Inverse der DCT-I ist die DCT-I mit einem Faktor von $2/(N-1)$ . Die Inverse der DCT-IV ist die DCT-IV mit einem Faktor $2/N$ . Die Inverse der DCT-II ist die DCT-III mit einem Faktor von $2/N$ oder umgekehrt.

Die Vorfaktoren der DCT sind in der Literatur nicht einheitlich festgelegt. Beispielsweise wird von manchen Autoren bei der DCT ein zusätzlicher Faktor von ${\sqrt {2/N}}$ eingeführt, um den zusätzlichen Faktor bei der inversen Operation zu vermeiden. Durch geeignete Wahl des konstanten Faktors kann die Transformationsmatrix eine orthogonale Matrix darstellen.

Mehrdimensionale DCT

Spektralkoeffizienten der zweidimensionalen DCT-II mit N₁=N₂=8

Insbesondere in der digitalen Bildverarbeitung spielt die zweidimensionale DCT, basierend auf der DCT-II, eine wesentliche Rolle. Die Erweiterung auf mehrere Dimensionen erfolgt im einfachsten Fall durch eine spalten- oder zeilenweise Anwendung der Transformation. Für praktische Implementierungen existieren zur Berechnung höherdimensionaler Transformationen effizientere Algorithmen.

$X_{{k_{1},k_{2}}}=\sum _{{n_{1}=0}}^{{N_{1}-1}}\sum _{{n_{2}=0}}^{{N_{2}-1}}x_{{n_{1},n_{2}}}\cos \left[{\frac {\pi }{N_{1}}}\left(n_{1}+{\frac {1}{2}}\right)k_{1}\right]\cos \left[{\frac {\pi }{N_{2}}}\left(n_{2}+{\frac {1}{2}}\right)k_{2}\right]$

Die rechte Abbildung zeigt als einfaches Beispiel alle Spektralkomponenten einer zweidimensionalen DCT-II mit in jeder Dimension acht Koeffizienten. Das Feld links oben (Index 0,0) stellt den Gleichanteil des Signals dar, in horizontaler Richtung sind die horizontalen Frequenzanteile aufsteigend. Über zwei Indizes hinweg wird die Frequenz verdoppelt. Gleiches gilt für die vertikale Richtung und für die Linearkombination aus den beiden Richtungen.

Anwendung von 2D-DCT

In JPEG wird jede Farb-Komponente (Y, Cb und Cr) des Bildes in 8×8-Blöcke eingeteilt, die einer 2D-DCT unterzogen werden.

Anwendung von 3D-DCT

In Filmformaten wird mitunter auch 3D-DCT angewendet. Dabei wird eineBildergruppe (group of pictures, GoP) von mehreren Bildern auch bezüglich der zeitlichen Veränderung betrachtet. Diese Methode findet zum Beispiel bei SoftCast Anwendung.

Anschauliches Beispiel einer iDCT

Ausgangsmaterial ist ein 8×8-Graustufenbild des Buchstaben A.

Originalgröße,

Zoom 10x (nächster Nachbar),

Zoom 10x (bilinear).

DCT des Bildes: ${\begin{bmatrix}6{,}1917&-0{,}3411&1{,}2418&0{,}1492&0{,}1583&0{,}2742&-0{,}0724&0{,}0561\\0{,}2205&0{,}0214&0{,}4503&0{,}3947&-0{,}7846&-0{,}4391&0{,}1001&-0{,}2554\\1{,}0423&0{,}2214&-1{,}0017&-0{,}2720&0{,}0789&-0{,}1952&0{,}2801&0{,}4713\\-0{,}2340&-0{,}0392&-0{,}2617&-0{,}2866&0{,}6351&0{,}3501&-0{,}1433&0{,}3550\\0{,}2750&0{,}0226&0{,}1229&0{,}2183&-0{,}2583&-0{,}0742&-0{,}2042&-0{,}5906\\0{,}0653&0{,}0428&-0{,}4721&-0{,}2905&0{,}4745&0{,}2875&-0{,}0284&-0{,}1311\\0{,}3169&0{,}0541&-0{,}1033&-0{,}0225&-0{,}0056&0{,}1017&-0{,}1650&-0{,}1500\\-0{,}2970&-0{,}0627&0{,}1960&0{,}0644&-0{,}1136&-0{,}1031&0{,}1887&0{,}1444\\\end{bmatrix}}$

allgemeine Basisfunktionen der diskreten Kosinustransformation entsprechen den speziell auf obiges Beispiel bezogenen Koeffizienten.

Jede einzelne DCT-Basisfunktion wird mit ihren aktuellen Koeffizienten multipliziert. Das so gewichtete Ergebnisbild wird zum fertigen Bild addiert.

Wiederherstellung eines 8×8-Graustufenbild des Buchstaben 'A' aus den gespeicherten DCT-Koeffizienten.
Links: Fertiges Bild,
Mitte: gewichtende Funktion, welche mit dem aktuellen Koeffizient multipliziert wurde und so zum fertigen Bild hinzugefügt wird
Rechts: allgemeine DCT-Basisfunktion und der aktuelle – auf das Beispiel bezogene – Koeffizient
Zoom: 10× bilinear

Die obige Darstellung wurde mittels bilinearem Zoom vergrößert Die sonst eckigen Pixel werden dadurch verschwommen dargestellt. Das fertige Bild ist nach wie vor ein 8×8-Graustufenbild mit möglicherweise mehr oder minder minimal abweichenden Farbwerten im Vergleich zum Original.

Literatur

Philipp W.Besslich, Tian Lu: Diskrete Orthogonaltransformationen. Springer Verlag, 1990, ISBN 3-540-52151-8.
Vladimir Britanak, Patrick C. Yip, K. R. Rao: Discrete Cosine and Sine Transforms: General Properties, Fast Algorithms and Integer Approximations. 1. Auflage. Academic Press, 2007, ISBN 978-0-12-373624-6.

Basierend auf einem Artikel in:

Wikipedia.de