Integralkosinus
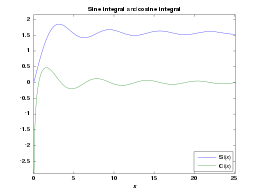
Graph
des Integralcosinus (grün, untere Kurve) und des Integralsinus (blau, obere
Kurve) für Argumente 0 ≤ x ≤ 8π
Der Integralkosinus ist eine Funktion, in deren Funktionsvorschrift ein Integral und die Kosinusfunktion auftreten. Diese Integralfunktion kann mit elementaren Methoden nicht ohne Integral dargestellt werden.
Der Integralkosinus ist definiert als:
Dabei ist
die Euler-Mascheroni-Konstante
Eigenschaften
- Das in der Definition auftretende Integral wird auch mit
bezeichnet:
- mit der Beziehung:
- Analog zur Ableitung des Integralsinus Si(x):
- gilt:
- Analog der komplexen Eulerformel-Definition des Cosinus
- gilt mit der Integralexponentialfunktion
.
- Es lässt sich eine überall konvergente Reihe angeben:
.
Anmerkung: In verschiedenen Formelsammlungen wird der Integralkosinus mit umgekehrten Vorzeichen definiert.
Eng verwandt ist der Integralsinus
,
der zusammen mit dem Integralcosinus
in parametrischer Darstellung eine Klothoide
bildet.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 18.05. 2021