Integralsinus

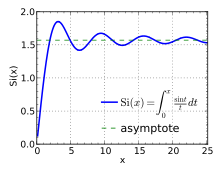
Verlauf des Integralsinus im Bereich 0 ≤ x ≤ 8π

Der Integralsinus ist ein Begriff aus der Mathematik und bezeichnet eine durch ein Integral gegebene Funktion. Joseph Liouville (1809–1882) bewies, dass der Kardinalsinus nicht elementar integrierbar ist.

Der Integralsinus ist definiert als das Integral der Sinc-Funktion:

$\operatorname {Si} (x):=\int _{0}^{x}\operatorname {si} (t)\,\mathrm {d} t=\int _{0}^{x}{\frac {\sin t}{t}}\,\mathrm {d} t$ .

Eigenschaften

Im Grenzübergang $\lim _{{x\to \infty }}{\mathrm {Si}}\left(x\right)$ kann das Integral ausgewertet werden. Es gilt:

$\lim _{{x\to \infty }}{\mathrm {Si}}\left(x\right)={\frac {\pi }{2}}$

Dies wird im Folgenden bewiesen:

$\lim _{x\to \infty }\mathrm {Si} \left(x\right)=\int _{0}^{\infty }{\frac {\operatorname {sin} (x)}{x}}\,\mathrm {d} x=\int _{0}^{\infty }\int _{0}^{\infty }\operatorname {sin} (x)\operatorname {exp} (-xy)\,\mathrm {d} y\,\mathrm {d} x=\int _{0}^{\infty }\int _{0}^{\infty }\operatorname {sin} (x)\operatorname {exp} (-xy)\,\mathrm {d} x\,\mathrm {d} y=\int _{0}^{\infty }{\frac {1}{y^{2}+1}}\mathrm {d} y={\frac {\pi }{2}}$

Sinus:

$\sin x={\frac {1}{2{\mathrm {i}}}}\left({\mathrm {e}}^{{{\mathrm {i}}x}}-{\mathrm {e}}^{{-{\mathrm {i}}x}}\right)$

gilt mit der Integralexponentialfunktion ${\mathrm {Ei}}$

${\mathrm {Si}}(x)={\frac {1}{2{\mathrm {i}}}}\left({\mathrm {Ei}}({\mathrm {i}}\ x)-{\mathrm {Ei}}(-{\mathrm {i}}\ x)\right)+{\frac {\pi }{2}}$

Die Entwicklung in eine Taylorreihe an der Stelle 0 liefert die kompakt konvergente Reihe:

${\mathrm {Si}}\left(x\right)=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}+\cdots \quad =\sum _{{k=0}}^{\infty }{\frac {(-1)^{{k}}}{(2k+1)!\cdot (2k+1)}}x^{{2k+1}}$