Schwache Ableitung

Eine schwache Ableitung ist in der Funktionalanalysis, einem Teilgebiet der Mathematik, eine Erweiterung des Begriffs der gewöhnlichen (klassischen) Ableitung. Er ermöglicht es, Funktionen eine Ableitung zuzuordnen, die nicht (stark bzw. im klassischen Sinne) differenzierbar sind.

Schwache Ableitungen spielen eine große Rolle in der Theorie der partiellen Differentialgleichungen. Räume schwach differenzierbarer Funktionen sind die Sobolev-Räume. Ein noch allgemeinerer Begriff der Ableitung ist die Distributionenableitung.

Definition

Schwache Ableitung für reelle Funktionen

Betrachtet man eine auf einem offenen Intervall I = (a,b) (klassisch) differenzierbare Funktion und eine Testfunktion $\varphi \in C_c^\infty(I)$ (das heißt, $\varphi$ ist beliebig oft differenzierbar und besitzt einen kompakten Träger), dann gilt

$\int_I f^\prime(t) \varphi(t) \,\mathrm{d}t = - \int_I f(t) \varphi^\prime(t) \,\mathrm{d}t$ .

Hierbei wurde die partielle Integration verwendet, wobei die Randterme auf Grund der Eigenschaften der Testfunktionen wegfallen $\left(\varphi(a) = 0, \varphi(b) = 0\right)$ .

Ist eine L^2 -Funktion, dann kann, selbst wenn nicht differenzierbar ist (genauer: keinen differenzierbaren Vertreter in der Äquivalenzklasse besitzt), eine Funktion $g \in L^2(I)$ existieren, die die Gleichung

$\int_I g(t) \varphi(t) \,\mathrm{d}t = - \int_I f(t) \varphi^\prime(t) \,\mathrm{d}t$

für jede Testfunktion $\varphi$ erfüllt. Eine solche Funktion heißt schwache Ableitung von . Man schreibt wie bei der klassischen Ableitung $f^\prime := g$ .

Höhere schwache Ableitungen

Sinngemäß zum oben beschriebenen Fall können schwache Ableitungen auch für Funktionen auf höherdimensionalen Räumen definiert werden. Entsprechend kann man auch die höheren schwachen Ableitungen definieren.

Es seien $\Omega\subseteq \R^n$ , $f \colon \Omega \rightarrow \R$ eine quadratisch integrierbare Funktion, das heißt, $f \in L^2(\Omega)$ , und $\alpha = (\alpha_1, \dotsc, \alpha_n) \in \N_0^n$ ein Multiindex.

Eine Funktion $g \in L^2(\Omega)$ heißt $\alpha$ -te schwache Ableitung von , falls für alle Testfunktionen $\varphi$ gilt:

$\int_{\Omega}g(x) \varphi(x)\, \mathrm{d}x = (-1)^{|\alpha|}\int_{\Omega}f(x) D^{\alpha}\varphi(x) \,\mathrm{d}x$ .

Hierbei ist $\textstyle |\alpha| = \sum_{i=1}^n\alpha_i$ und $D^{\alpha} = \frac{\partial^{|\alpha|}}{\partial^{\alpha_1}x_1\dotso\partial^{\alpha_n}x_n}$ . Häufig schreibt man $g = D^{\alpha} f$ .

Man kann statt $f, g \in L^2$ auch allgemeiner $f, g \in L^p$ für $1 \leq p \leq \infty$ fordern. Die Teilmenge der Funktionen aus L^p , in der $n \geq 1$ schwache Ableitungen existieren, ist ein sogenannter Sobolev-Raum.

Liegt eine Funktion $f \colon \Omega \rightarrow \R^m$ vor, so fordert man die schwache Differenzierbarkeit in jeder der Bildkomponenten.

Erweiterungen

Die Definition der schwachen Ableitung lässt sich auf unbeschränkte Mengen $\left(\right.$ also ganz $\R$ oder $\R^n\left.\right)$ , Räume periodischer Funktionen oder Räume auf der Kugel oder höherdimensionalen Sphären erweitern.

In einer weiteren Verallgemeinerung lassen sich auch Ableitungen gebrochener Ordnung gewinnen.

Eigenschaften

Eindeutigkeit

Die schwache Ableitung ist, wenn sie existiert, eindeutig: Gäbe es zwei schwache Ableitungen g_1 und g_2 , dann müsste nach der Definition

$\int_I (g_1(t) - g_2(t)) \varphi(t) \,\mathrm{d}t = 0$

für alle Testfunktionen $\varphi$ gelten, was aber nach dem Lemma von Du Bois-Reymond g_1 = g_2 bedeutet (im L^2 -Sinne, d.h. fast überall), da die Testfunktionen dicht in L^p liegen (für $1 \leq p < \infty$ ).

Beziehung zur klassischen (starken) Ableitung

Bei jeder klassisch differenzierbaren Funktion existiert die schwache Ableitung und stimmt mit der klassischen Ableitung überein, so dass man von einer Verallgemeinerung des Ableitungsbegriffs sprechen kann. Im Gegensatz zur klassischen Ableitung ist die schwache Ableitung aber nicht punktweise, sondern nur für die ganze Funktion definiert. Punktweise muss eine schwache Ableitung nicht einmal existieren. Gleichheit ist daher im L^2 -Sinne zu verstehen, d.h. zwei Funktionen sind genau dann gleich, wenn $||f-g||_{L^2}=0$ gilt.

Es lässt sich zeigen, dass hinreichend oft vorhandene schwache Differenzierbarkeit auch wieder Differenzierbarkeit im klassischen Sinne nach sich zieht. Dies ist gerade die Aussage des Einbettungssatz von Sobolew: Unter gewissen Bedingungen existieren Einbettungen eines Sobolew-Raums mit schwachen Ableitungen in Räume -fach differenzierbarer Funktionen C^k mit $n > k \ge 0$ .

Existenz

Eine absolutstetige Funktion besitzt eine schwache Ableitung.

Beispiele

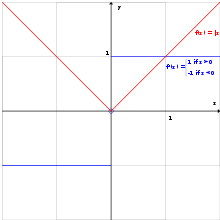
Schwache Ableitung Absolutbetrag

Die Betragsfunktion f(x) = |x| (vgl. Beispiel nicht differenzierbare Funktion) ist in jedem Punkt außer x = 0 klassisch differenzierbar und besitzt daher in dem Intervall ]a,b[ für a<0<b keine klassische Ableitung. Allerdings gilt für $f^\prime\colon]a,b[\to\R$ mit

$f^\prime(x) = \begin{cases} -1 &: x < 0\\ 0 &: x = 0\\ +1 &: x > 0 \end{cases}$

und einer beliebigen Testfunktion $\varphi\colon]a,b[\to\R$ gerade

$\begin{align} \int_a^b\varphi'(x)\cdot f(x) \,\mathrm{d}x=&\int_a^0-\varphi'(x)x \,\mathrm{d}x+\int_0^b\varphi'(x)x \,\mathrm{d}x\\=&-\left(\int_a^0\varphi(x)\cdot (-1)\,\mathrm{d}x+\int_0^b\varphi(x)\cdot 1\,\mathrm{d}x\right)\\ =&-\int_a^b\varphi(x)\cdot f^\prime(x)\,\mathrm{d}x. \end{align}$

Somit ist $f^\prime$ eine schwache Ableitung von .

Da $\{0\}$ eine Nullmenge ist und daher bei der Integration unbedeutend ist, kann man den Wert an der Stelle 0 beliebig setzen. Die oben gewählte Ableitung ist die Signumfunktion. Die Signumfunktion selbst ist nicht mehr schwach differenzierbar, aber man kann sie im Sinne von Distributionen ableiten.

Anwendungen

Schwache Ableitungen werden systematisch untersucht in Sobolew-Räumen und zum Beispiel bei der Lösung von partiellen Differentialgleichungen verwendet.

Basierend auf einem Artikel in:

Wikipedia.de