Magma (Mathematik)

berührt die Spezialgebiete

Mathematik

umfasst als Spezialfälle

Halbgruppe (Axiome EA)
- Monoid (EAN)
  - Gruppe (EANI)
    - Abelsche Gruppe (EANIK)
- kommutative Halbgruppe (EAK)
  - kommutatives Monoid (EANK)
    - natürliche Zahlen (N,+)
Quasigruppe (Gleichungen auflösbar)

In der Mathematik ist ein Magma (neutrum, Mehrzahl Magmen) eine algebraische Struktur, bestehend aus einer Menge zusammen mit einer zweistelligen inneren Verknüpfung. Es wird auch Gruppoid ^[1], manchmal Binar oder Operativ genannt.

Eine Verallgemeinerung des Magmas ist das Pseudo-Magma, in dem die Verknüpfung nicht mehr auf der ganzen zugrundeliegenden Menge erklärt sein muss, also partiell sein kann.

Definitionen

Magma

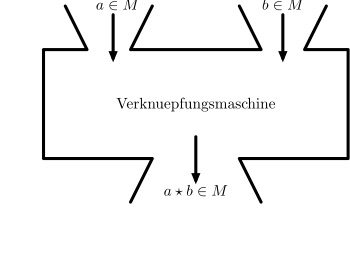
Eine Verknüfung mit zwei Eingängen und einem Ausgang

Ein Magma ist ein Paar (M,*), bestehend aus einer Menge (der Trägermenge) und einer zweistelligen inneren Verknüpfung $*\,\colon \,M\times M\rightarrow M.$

Für a*b , die Verknüpfung zweier Elemente $a,b\in M$ , schreibt man auch kurz .

Die leere Menge kann auch als Trägermenge zugelassen werden; sie ist auf triviale Weise ein Magma.

Ist die Verknüpfung kommutativ, so heißt das Magma kommutativ oder abelsch; ist sie assoziativ, so heißt das Magma assoziativ oder Halbgruppe.

Untermagma

Sei ${\boldsymbol {M}}=(M,*)$ ein Magma. Ein Magma ${\boldsymbol {U}}=(U,\circ )$ heißt Untermagma von ${\boldsymbol {M}}$ , wenn $U\subseteq M$ und $\circ =*|_{U\times U}$ , d.h., die Verknüpfung $\circ$ ist die Einschränkung von auf $U\times U$ .

Genau dann ist also ${\boldsymbol U}$ ein Untermagma von ${\boldsymbol {M}}$ , wenn $U\subseteq M$ und abgeschlossen ist bezüglich , d.h., es gilt

$a\circ b=a*b\in U$ für alle $a,b\in U$ .

${\boldsymbol {M}}$ nennt man dann auch Obermagma von ${\boldsymbol U}$ .

Der Durchschnitt von Untermagmen ist ein Untermagma.
Jede Teilmenge $U\subset M$ eine Magmas ist enthalten in einem kleinsten Untermagma, das enthält. Dieses Untermagma heißt von erzeugt.

Beispiele

Die folgenden Beispiele sind Magmen, die keine Halbgruppen sind:

$(\mathbb {Z} ,-)$ : die ganzen Zahlen mit der Subtraktion
$(\mathbb {R} \setminus \{0\},/)$ : die reellen Zahlen ungleich $0$ mit der Division
Die natürlichen Zahlen mit der Exponentiation, also mit der Verknüpfung $a*b=a^{b}$
Die reellen Zahlen mit der Bildung des arithmetischen Mittels als Verknüpfung
Alle Gleitkommadarstellungen (Gleitkommazahl) zu beliebigen Basen, Exponenten- und Mantissen-längen mit der Multiplikation sind echte, unitäre, kommutative Magmen wenn man (der Abgeschlossenheit wegen) die NaNs und ∞ hinzunimmt. So ist die Gleitkommamultiplikation weder assoziativ noch besitzt sie im Allgemeinen ein eindeutiges Inverses, auch wenn beides für einige Fälle tatsächlich gilt.
Endliche Magmen werden oft mit Verknüpfungstafeln dargestellt, z. B. für das Magma $A=(\{a,b,c,d\},*)$ :

	a	b	c	d
a	a	b	c	a
b	c	d	b	c
c	c	a	a	c
d	a	d	d	b

Die folgenden Beispiele sind keine Magmen, da die angegebene Verknüpfung nicht für alle möglichen Werte definiert ist (sie sind also Pseudo-Magmen):

Die natürlichen Zahlen mit der Subtraktion.
Die reellen Zahlen mit der Division.
Alle Gleitkommamultiplikationen ohne NaNs oder ∞.

Beispiele für Untermagmen sind

$(\mathbb {Q} \setminus \{0\},/)$ (die rationalen Zahlen ungleich $0$ mit der Division) ist ein Untermagma von $(\mathbb {R} \setminus \{0\},/)$ (siehe oben).
Das Magma $B=(\{a,c\},\circ )$ mit folgender Verknüpfungstafel ist Untermagma des oben genannten Magmas $A=(\{a,b,c,d\},*)$ :

$\circ$	a	c
a	a	c
c	c	a

Eigenschaften

Die Grundmenge ist unter einer inneren Verknüpfung per Definition abgeschlossen. Ansonsten muss ein Magma keine speziellen Eigenschaften haben. Durch Hinzunahme weiterer Bedingungen werden speziellere Strukturen definiert, die alle wiederum Magmen sind. Typische Beispiele sind:

Halbgruppe: ein Magma, dessen Verknüpfung assoziativ ist
Monoid: eine Halbgruppe mit einem neutralen Element
Quasigruppe: ein Magma, in dem alle Gleichungen der Form oder eindeutig nach auflösbar sind
Loop: eine Quasigruppe mit einem neutralen Element
Gruppe: ein Monoid, in dem jedes Element ein Inverses hat
Abelsche Gruppe: eine Gruppe, deren Verknüpfung kommutativ ist
Mediales Magma: ein Magma, in dem für alle Elemente die Gleichung $(a\star b)\star (c\star d)=(a\star c)\star (b\star d)$ gilt

Morphismen

Sind $(A,\star ),(B,\circ )$ zwei Magmen, so heißt eine Abbildung $f\colon A\rightarrow B$ ein Morphismus, wenn für alle $a,a'\in A$ gilt: $f(a\star a')=f(a)\circ f(a')$ .

Ist $A=B$ , so heißt $f\colon A\rightarrow A$ Endomorphismus.
Ist ein Morphismus $f\colon A\rightarrow B$ als Abbildung bijektiv, so ist auch die Umkehrabbildung ein Morphismus. In diesem Fall heißt ein Isomorphismus.

Beispiele für Morphismen

Die Identität auf einem Magma ist stets ein Morphismus.
Die Verkettung von Morphismen ist ein Morphismus. Die Klasse der Magmen zusammen mit der Klasse der Morphismen bilden eine Kategorie .
Hat ein Magma nur ein Element, so gibt es von jedem Magma genau einen Morphismus $f\colon A\rightarrow E$ .
Im obigem Beispiel gibt es nur einen Morphismus . Ist ein Morphismus, so folgt:
- $f(a)=f(a\star a)=f(a)\circ f(a)$ . Es kommt daher nur $f(a)=a$ in Frage.
- Da ein kommutatives Magma ist, folgt $f(b)=f(a\star b)=f(b\star a)=f(c)$ . Angenommen es ist $f(b)=c$ . In diesem Fall folgt einerseits $f(d)=f(b\star b)=c\circ c=a$ . Andererseits folgt $f(d)=f(d\star b)=a\circ c=c$ . Das ist ein Widerspruch. Also ist $f(b)=f(c)=a$ . Es folgt nun: $f(d)=a$ .

Freies Magma

Für jede nichtleere Menge kann man das freie Magma über definieren als die Menge aller endlichen Binärbäume, deren Blätter mit Elementen von beschriftet sind. Das Produkt zweier Bäume und ist der Baum, dessen Wurzel den linken Unterbaum und den rechten Unterbaum hat. Aufschreiben kann man die Elemente des freien Magmas durch vollständig geklammerte Ausdrücke.

Sei zum Beispiel $X=\{a,b,c\}.$ Dann enthält das freie Magma über unter anderem die paarweise verschiedenen Elemente

$a,\,b,\,c,\,ab,\,ba,\,(ab)c,\,a(bc),\,(aa)(bb),\,(a(ab))b,\,(ab)(ab).$

Anmerkungen

↑ Die Bezeichnung Gruppoid wird auch für eine mathematische Struktur in der Kategorientheorie verwendet, Gruppoid (Kategorientheorie).

Basierend auf einem Artikel in:

Wikipedia.de