
Differenzenmenge
Eine Differenzenmenge der Ordnung n
(englisch: perfect difference set)
ist in der endlichen
Geometrie eine Menge von
natürlichen
Zahlen[1],
aus der sich eine eindeutige projektive
Ebene erzeugen lässt. James Singer konnte in den 1930er Jahren beweisen, dass jede endliche desarguessche Ebene
von einer Differenzenmenge abstammt.
Diese Tatsache ist eine der Aussagen des Satzes von Singer, der darüber
hinaus besagt, dass jede endliche desarguessche projektive
Geometrie einen Singer-Zyklus besitzt. Es wird vermutet, ist aber
(2012) noch nicht bewiesen, dass genau die desarguesschen endlichen
Ebenen von einer Differenzenmenge abstammen.
Definitionen
Es sei n eine natürliche Zahl. Eine Menge
von natürlichen Zahlen heißt eine Differenzenmenge der Ordnung n, falls
gilt
enthält genau
Elemente,
- jede natürliche Zahl
lässt sich auf genau eine Weise schreiben als
mit
Die zweite Bedingung lässt sich formal abschwächen. Sei
die Diagonale in
.
Dann ist die 2. Bedingung zunächst gleichwertig zu der abstrakter formulierten
Bedingung
Da für eine Menge ,
die der 1. Bedingung gemäß
Elemente enthält, die Menge
der Paare unterschiedlicher Zahlen immer
Elemente enthält, ist die Definitionsmenge von
immer gleichmächtig zur Zielmenge, daher sind für diese Abbildung Surjektivität, Injektivität
und Bijektivität gleichwertige Forderungen und die 2. Bedingung kann durch
- (2b) „Für
sind die Differenzen
paarweise verschiedene Zahlen (mit anderen Worten:
ist injektiv).“ oder durch
- (2c) „Jede natürliche Zahl
tritt modulo
als Differenz
auf (mit anderen Worten:
ist surjektiv).“
ersetzt werden.
Reduzierte Differenzenmenge
- Ist
eine Differenzenmenge der Ordnung
, dann sind auch die
verschiedenen Mengen
für beliebige
solche Differenzenmengen.
- Jede Differenzenmenge
der Ordnung
enthält genau zwei verschiedene Elemente
mit
Dann ist
ebenfalls eine solche Differenzenmenge.
Singer verwendet Differenzenmengen, die 0 und 1 enthalten und deren Elemente
alle in
liegen, als Normalformen für Differenzenmengen und bezeichnet eine solche
Differenzenmenge dann als reduzierte Differenzenmenge (englisch:
reduced perfect difference set).
Beutelspacher und Rosenbaum verwenden als Normalenform Mengen, die 1 und 2
enthalten und deren Elemente alle in
liegen, ohne dafür eine gesonderte Bezeichnung einzuführen.
Es gilt:
- Falls eine Differenzenmenge der Ordnung
existiert, dann existiert auch eine solche, die 0 und 1 enthält (also eine reduzierte Differenzenmenge), der Ordnung
.
Eigenschaften und Bedeutung
Projektive Ebene
Ist
eine Differenzenmenge der Ordnung
,
dann ist die folgendermaßen definierte Geometrie
eine projektive Ebene der Ordnung
:
- Die Punktmenge ist die Menge
von natürlichen Zahlen,
- die Geradenmenge
besteht aus den Teilmengen
,
- die Inzidenzrelation
von
ist die mengentheoretische Enthaltenrelation zusammen mit ihrer Umkehrung:
Man sagt dann: Die so definierte projektive Ebene
„stammt von der Differenzenmenge
“
ab.
Singer-Zyklus, Satz von Singer
Sei
eine Kollineation auf einer
endlichen projektiven Geometrie. Wenn
die Punkte und Hyperebenen der Geometrie zyklisch permutiert, das heißt im Falle
einer endlichen Ebene
der Ordnung
:
wenn für beliebige
gilt
dann heißt die von
erzeugte Kollineationsgruppe
ein Singer-Zyklus der Geometrie, speziell der Ebene.
Der Satz von Dembowski-Hughes-Parker besagt, dass eine Gruppe von Kollineationen einer projektiven Geometrie genau dann auf der Punktmenge transitiv operiert, wenn sie auf der Menge der Hyperebenen transitiv operiert. Daraus folgt, dass die geforderten Eigenschaften (1) und (2) für zyklische Kollineationsgruppen auf einer Ebene äquivalent sind.
Die folgenden Aussagen werden als Satz von Singer bezeichnet:
- Jede endliche, desarguessche, projektive Geometrie besitzt einen Singer-Zyklus. Dieser kann so gewählt werden, dass er sogar nur aus Projektivitäten besteht.
- Eine endliche projektive Ebene besitzt genau dann einen Singer-Zyklus, wenn sie isomorph zu einer von einer Differenzenmenge abstammenden Ebene ist.
Ist
eine solche Ebene in ihrer oben beschriebenen Darstellung durch die
Differenzenmenge
,
dann ist
eine Kollineation der Ordnung
,
die somit einen Singer-Zyklus erzeugt.
Konstruktion von Singer-Zyklen auf einer desarguesschen Geometrie
Jede desarguessche projektive Geometrie endlicher Ordnung ist isomorph zu
einem -dimensionalen
projektiven
Raum
über einem endlichen
Körper
.
Der Koordinatenvektorraum
von
ist als
-Vektorraum
isomorph zu dem endlichen Körper
.
Die multiplikative Gruppe
ist zyklisch,
also existiert ein erzeugendes („primitives“) Element
dieser Gruppe, mit dem
gilt. Die Abbildung
ist ein -Vektorraumautomorphismus.
Nach Wahl einer Punktbasis in
kann dieser Automorphismus als Koordinatendarstellung
einer Projektivität
angesehen werden. Da
transitiv auf
operiert, operiert auch die dadurch dargestellte Projektivität transitiv auf
der Punktmenge von
und erzeugt daher einen Singer-Zyklus dieser projektiven Geometrie.
Beispiele
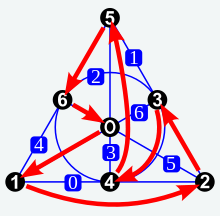
- Die Menge
ist eine Differenzenmenge der Ordnung 2, denn die sämtlichen Differenzen von verschiedenen Elementen
lauten (modulo 7):
-
- Die 7 Geraden der projektiven Ebene zu dieser Differenzenmenge lauten,
vergleiche auch die Abbildung rechts:
- Die Ebene ist isomorph zur Fano-Ebene.
- Die Mengen
bzw.
sind Differenzenmengen der Ordnung 3 bzw. 4.
- Die Menge
ist eine reduzierte Differenzenmenge der Ordnung 5.
- Da zu den Ordnungen 6, 10, 12 und 14 keine projektiven Ebenen existieren, gibt es auch keine Differenzenmengen dieser Ordnungen.
- Der Satz von Bruck-Ryser-Chowla liefert notwendige Bedingungen an die Ordnungen projektiver Ebenen. Natürliche Zahlen, die nach diesem Satz ausgeschlossen sind (Folge A046712 in OEIS), können auch nicht Ordnungen einer Differenzenmenge sein.
Literatur
- Albrecht Beutelspacher, Ute Rosenbaum: Projektive Geometrie. Von den Grundlagen bis zu den Anwendungen (= Vieweg Studium: Aufbaukurs Mathematik). 2., durchgesehene und erweiterte Auflage. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X
Anmerkungen
- ↑
Im vorliegenden Artikel wird die 0 stets zu den
natürlichen Zahlen
gezählt.
- ↑
Man beachte dazu, dass
aufgrund der Eigenschaften der Modulo-Funktion mod stets eine Abbildung ist.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.12. 2019