
Kellerautomat
Ein Kellerautomat (KA, auch PDA für englisch pushdown automaton; auch Stackmaschine) ist ein Automat im Sinne der theoretischen Informatik, ein Konstrukt, das verwendet wird, um gewisse Eigenschaften von Problemen und Algorithmen zu analysieren und zu beweisen.
Der Kellerautomat ist ein endlicher Automat, der um einen Kellerspeicher (a.g. Stack) erweitert wurde. Ein Kellerautomat mit zwei Kellerspeichern ist gleichmächtig zur Turingmaschine.
Funktionsweise
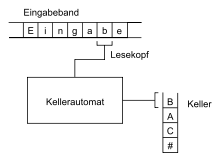
Ein Kellerautomat dient dazu, zu klären, ob eine Eingabe (d.h. ein Wort aus null, einem oder mehreren Zeichen) zu einer bestimmten formalen Sprache (d.h. einer Menge von Wörtern) gehört. Dafür arbeitet der Automat das Eingabewort Schritt für Schritt von links nach rechts ab und kann dabei eine Reihe von Zuständen annehmen. Zu Anfang ist er im sogenannten Startzustand. Typischerweise wird in jedem Verarbeitungsschritt ein Zeichen aus der Eingabe gelesen. Außerdem wird in jedem Verarbeitungsschritt das oberste Zeichen vom Keller gelesen, d.h. entfernt. Abhängig vom aktuellen Zustand, dem gerade gelesenen Eingabezeichen und dem gerade gelesenen Kellerzeichen geht der Automat in einen neuen Zustand über und legt anstelle des entfernten Kellerzeichens ein neues Wort auf dem Keller ab. Wenn die gesamte Eingabe gelesen wurde und der Keller leer ist, gehört die Eingabe zur vom Automaten erkannten Sprache.
Allgemein sind allerdings mehrere Abweichungen von der obigen Erklärung möglich:
- Die erkannte Sprache kann auch als die Menge der Wörter definiert werden, bei deren Abarbeitung der Kellerautomat einen sogenannten Endzustand erreicht – unabhängig davon, ob dabei der Keller geleert wird.
- Nicht in jedem Verarbeitungsschritt muss ein Zeichen aus der Eingabe
gelesen werden. Wenn keins gelesen wurde, wird das gelesene Wort als
(das leere Wort) bezeichnet.
- Für manche Kombinationen von Zustand, Eingabezeichen (oder
) und Kellerzeichen kann der Kellerautomat die Wahl zwischen mehreren Übergängen (also Kombinationen von Folgezustand und Kellerwort) haben. Die Eingabe gilt in diesem Fall als erkannt, wenn der Keller geleert werden kann bzw. ein Endzustand erreicht werden kann.
Beispiel
Um das Prinzip eines Kellerautomaten zu verdeutlichen, wird häufig die syntaktische Untersuchung geklammerter Ausdrücke herangezogen. Beispielsweise muss in einem Ausdruck einer bestimmten Sprache zu jeder öffnenden Klammer auch eine schließende Klammer existieren:
- Beispiel: { … { … } … }
Der Automat beginnt in einem Startzustand z0; im Keller befindet sich ein Zeichen, welches das Ende kennzeichnet (#). Bei der Abarbeitung des Ausdrucks bewegt sich der Lesekopf Zeichen für Zeichen weiter. Stößt er dabei auf eine öffnende Klammer, so wird diese in den Keller geschrieben. Tritt in der weiteren Abarbeitung eine schließende Klammer auf, so wird das oberste Klammer-auf-Zeichen im Keller wieder gelöscht. Der Ausdruck ist dann erfolgreich abgearbeitet, wenn der Lesekopf das Ende des Eingabebandes erreicht hat und sich im Keller ausschließlich das Zeichen # befindet. Befände sich hingegen noch eine geöffnete Klammer nach der Ausdrucksabarbeitung im Keller, so würde dies bedeuten, dass eine schließende Klammer fehlt und ein syntaktischer Fehler vorliegt. Auch wenn das Ende des Kellers erreicht wird, bevor die Eingabe vollständig abgearbeitet wurde, liegt ein Fehler vor. In diesem Fall befinden sich zu viele schließende Klammern in der Eingabe.
Formale Definition
Ein nichtdeterministischer Kellerautomat (NKA) wird definiert als ein
7-Tupel ,
wobei
eine endliche Menge von Zuständen,
ein Eingabealphabet,
das Kelleralphabet,
die Zustandsübergangsfunktion,
, die nur auf endliche Teilmengen von
abbildet,
der Startzustand,
das Anfangssymbol im Keller und
eine Menge von Endzuständen
ist.
Dabei bezeichnet
das leere Wort und
die Menge der Wörter des Alphabets
.
Manchmal findet man auch Kellerautomaten als 6-Tupel
,
in diesem Fall gibt es keine Endzustände, und der Kellerautomat akzeptiert ein
Wort, falls nach der Abarbeitung des Wortes der Keller leer ist.
Wenn die Übergangsfunktion die Eigenschaft
erfüllt, spricht man von einem deterministischen Kellerautomaten. Zu
einer festen Eingabe gibt es dann höchstens eine Zustandsübergangsabfolge,
Mehrdeutigkeiten können also nicht auftreten.
Anmerkungen
- Für einen nichtdeterministischen Kellerautomaten ist es möglich, in der Definition auf die Menge der Endzustände zu verzichten. Stattdessen definiert man, dass der nichtdeterministische Kellerautomat seine Eingabe akzeptiert, wenn es einen Berechnungspfad gibt, bei dem nach dem Einlesen der Eingabe der Keller das leere Wort enthält. Die beiden Definitionen sind hinsichtlich der akzeptierten Sprachen äquivalent. Für einen deterministischen Kellerautomaten ist diese Aussage im Allgemeinen jedoch falsch. Der deterministische Kellerautomat, der über Endzustände akzeptiert, ist mächtiger.
- Das heißt, dass ein deterministischer Kellerautomat terminieren kann, sobald ein Endzustand erreicht wurde, aber nicht sofort terminieren muss. Dabei spielt der Keller keine Rolle. Er akzeptiert ein Wort, wenn er terminiert und das Eingabewort leer ist. Ist es nicht leer und es sind keine Regeln mehr anwendbar, wurde es nicht akzeptiert.
- Für einen solchen bei leerem Keller akzeptierenden nichtdeterministischen Kellerautomaten ist es möglich, einen äquivalenten Kellerautomaten mit einem einzigen Zustand zu konstruieren, indem die Zustände des alten Kellerautomaten vollständig im Keller des neuen Kellerautomaten simuliert werden. In der Definition eines nichtdeterministischen Kellerautomaten kann also neben der Menge der Endzustände auch zusätzlich auf den Startzustand und die Zustandsmenge verzichtet werden.
- Es kann in der Definition eines nichtdeterministischen Kellerautomaten auf
-Übergänge verzichtet werden. Die Zustandsübergangsfunktion ist dann ein Element aus
. Mit Hilfe der Greibach-Normalform zeigt man, dass zu jedem nichtdeterministischen Kellerautomaten ein äquivalenter nichtdeterministischer Kellerautomat ohne
-Übergänge existiert.
Akzeptierte Sprache
Die Menge der Konfigurationen eines Kellerautomaten ist .
Ein Element
dieser Menge besteht aus
- dem aktuellen Zustand
,
- dem noch zu lesenden Wort
sowie
- dem Kellerinhalt
.
Auf
wird eine Relation
definiert, über die im Anschluss festgelegt wird, welche Worte akzeptiert
werden. Es ist
Für Automaten, deren Endzustandsmengen über die Akzeptanz entscheiden sollen, heißt es dann:
wird von
genau dann akzeptiert, wenn es ein
sowie ein
gibt, sodass
.
Für Automaten hingegen, bei denen die Akzeptanz davon abhängt, ob der Keller leer ist, lautet die Formulierung:
wird von
genau dann akzeptiert, wenn es ein
gibt, sodass
oder
.
Dabei ist >
die reflexive
und transitive
Hülle
von
.
Beispiel
Der folgende Kellerautomat M ist deterministisch und erkennt die kontextfreie
Sprache :
| Parameter | Funktionswert | ||||
|---|---|---|---|---|---|
| Zustand | Eingabe | Keller | Zustand | Keller | |
| z0 | a | # | z0 | a# | (1) |
| z0 | a | a | z0 | aa | (2) |
| z0 | b | a | z1 | ε | (3) |
| z1 | b | a | z1 | ε | (4) |
| z1 | ε | # | z2 | ε | (5) |
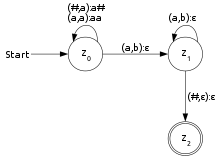
- (1), (2) Im Zustand z0 werden die führenden a-Zeichen der Eingabe gelesen und im Keller gespeichert.
- (3) Bei Eingabe b und einem a als oberstes Kellerelement erfolgt ein Zustandswechsel von z0 zu z1. Abgleich im Keller erfolgt. (Abgleich bedeutet "Löschen" des obersten Stack-Elementes bzw. Stack "pop")
- (4) Alle weiteren b-Zeichen werden gelesen, sofern noch genügend a-Zeichen im Keller gespeichert sind. Der Keller wird abgeglichen.
- (5) Wenn sich nur noch das Anfangssymbol
im Keller befindet und keine Eingabe erfolgt, geht der Kellerautomat in den Endzustand z2 über und akzeptiert damit die Eingabe.
Erhält der Kellerautomat beispielsweise die Eingabe aabb, so durchläuft er folgende Konfigurationen:
(die hochgestellte Nummer am Pfeil kennzeichnet die benutzte Zustandsübergangsfunktion)
(z0, aabb, #) ⇝(1) (z0, abb, a#) ⇝(2) (z0, bb, aa#) ⇝(3) (z1, b, a#) ⇝(4) (z1, ε, #) ⇝(5) (z2, ε, ε)
Dieser Kellerautomat M kann grundsätzlich, wenn er begonnen hat, den Keller zu lesen, nicht wieder schreiben. Daher ist die erkannte Sprache insbesondere auch eine lineare Sprache.
Kellerautomaten und formale Sprachen
Ein (Keller-)Automat liest eine aus einzelnen Zeichen bestehende Eingabe und akzeptiert (oder erkennt) diese – oder auch nicht. Die Menge der akzeptierten Eingaben bildet die durch den Automaten definierte Sprache.
Der nichtdeterministische Kellerautomat erkennt genau die kontextfreien Sprachen (Typ 2, vgl. Chomsky-Hierarchie). Er ist damit mächtiger als endliche Automaten, welche genau die regulären Sprachen (Typ 3) erkennen, aber weniger mächtig als Turingmaschinen, welche genau die rekursiv aufzählbaren Sprachen (Typ 0) erkennen. Ein deterministischer Kellerautomat (DPDA) erkennt die deterministisch-kontextfreien Sprachen, also nur eine echte Teilmenge der kontextfreien Sprachen.
Die Bedeutung des Kellerautomaten ergibt sich also daraus, dass sich Erkenntnisse über diesen (beispielsweise Äquivalenz mit anderen Automaten) auf die kontextfreien Sprachen übertragen lassen (und umgekehrt).
Praktische Implementierung eines Kellerautomaten
Als praktisches Anwendungsbeispiel eines Kellerautomaten sei folgender Parser (implementiert in C) gegeben, welcher eine Sprache, die aus Klammerpaaren besteht, parst und auf Richtigkeit prüft. Der Ausdruck ()((()())) würde beispielsweise akzeptiert werden, falsch hingegen wäre (()())), da hier eine schließende Klammer zu viel gegeben ist.
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#define POP -1
#define ACCEPT -2
#define ERROR -3
#define ALPHABET 3 /* Größe des Eingabealphabets */
#define MAX_LEN 80
/*
Ein einfacher Kellerautomat ("pushdown automaton")
Symbol | ( | ) | \0
---------+---------+--------+-----------
State 0 | PUSH 1 | ERROR | ACCEPT
State 1 | PUSH 1 | POP | ERROR
*/
int states[2][ALPHABET*2] =
{
{
'(', 1 /* PUSH 1 */,
')', ERROR,
'\0', ACCEPT
},
{
'(', 1 /* PUSH 1 */,
')', POP,
'\0', ERROR
}
};
int main( int argc, char** argv )
{
int stack[100] = { 0 };
int i = 0;
int action = 0;
int* tos = stack;
char s [MAX_LEN+1];
char* p = s;
/* Eingabe-Zeichenkette */
printf("Bitte Ausdruck eingeben: ");
fgets(s, sizeof(s), stdin);
s[strlen(s)-1]='\0'; /* Zeilenvorschub (NL) von fgets() durch binäre Null ersetzen */
/* Startzustand auf Stack ("push") */
*(tos++) = 0;
/* Ausführungsschleife */
do
{
/* Aktion auf Basis des Eingabesymbols ermitteln */
action = ERROR;
for( i = 0; i < ALPHABET; ++i )
{
if( states[*(tos-1)][i*2] == *p )
{
action = states[*(tos-1)][i*2+1];
break;
}
}
/* Ausführen der Aktionen */
if( action == ERROR )
{
printf("Unerwartetes Zeichen an Position %d\n", p-s);
break;
}
else if( action == ACCEPT )
printf("Ausdruck akzeptiert!\n");
else if( action == POP )
--tos;
else
*(tos++) = action;
/* Eingabe erweitern... */
++p;
}
while( action != ACCEPT );
return 0;
}
Anwendungen in Technik und Wissenschaft
Die Gleitkommaeinheit (engl. Floating Point Unit, FPU) der Intel-32-Bit x86-Architektur ist ursprünglich als Kellerautomat (engl. Stack Machine) realisiert. Ihr Kellerspeicher besitzt eine Tiefe von 8 Speicherplätzen (für jeweils einen 80-Bit-Gleitkommawert). Angesichts der Einschränkungen durch das Kellermodell ist tendenziell jedoch erkennbar, dass künftig auch im PC – wie in anderen Rechnerarchitekturen üblich – vorwiegend Verarbeitungseinheiten mit direkt adressierbaren Registern verwendet werden (SIMD-Erweiterung).
Compiler oder Interpreter von Programmiersprachen können mit Hilfe von Kellerautomaten entwickelt werden. Der Kellerautomat dient dabei der Syntaxanalyse, das heißt, er überprüft die syntaktische Korrektheit einer Tokenfolge.
Siehe auch
- Registermaschine
- umgekehrte polnische Notation (Postfix-Notation)
- Compiler


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.10. 2022