Leeres Wort

Das leere Wort ist in der Theoretischen und in der Praktischen Informatik ein Wort, das aus keinem einzigen Zeichen besteht, also die Länge 0 hat. Es wird auch Leerstring genannt. In vielen Programmiersprachen wird ein solcher String durch ein Literal dargestellt, bei dem die beiden Anfangs- und Endzeichen, die eine Zeichenkette einschließen, unmittelbar aufeinander folgen, z.B. "" in Perl oder Java.

Definition

Das leere Wort über dem Alphabet $\Sigma$ ist eine Folge von Elementen aus $\Sigma$ der Länge 0.

Schreibweise

Das leere Wort wird meist mit dem griechischen Buchstaben $\varepsilon$ (Epsilon für Englisch „empty“) dargestellt, oft findet sich dafür aber auch der griechische Buchstabe $\lambda$ (Lambda, vom Deutschen „leer“). Andere übliche Darstellungen sind $\epsilon$ als andere Schreibweise des Epsilon, (ebenfalls für „empty“) und als Einselement eines multiplikativ geschriebenen Monoids.

Merkmale

$|\varepsilon |=0$

Die Länge des leeren Wortes ist stets 0. Diese Eigenschaft folgt direkt aus der Definition.

$\forall w\in \Sigma ^{*}:\varepsilon w=w\varepsilon =w$

Das leere Wort bildet bei der Konkatenation von Wörtern das neutrale Element, sprich, die Verkettung eines beliebigen Wortes über ein beliebiges Alphabet $\Sigma$ mit $\varepsilon$ ergibt stets wieder . Die Menge der Wörter, welche über dem Alphabet gebildet werden können, ist die Kleenesche Hülle $\Sigma ^{*}$ .

$\varepsilon \in \Sigma^*$

Das leere Wort $\varepsilon$ ist Element der Kleeneschen Hülle $\Sigma ^{*}$ über jedes beliebige Alphabet $\Sigma$ . Anders ausgedrückt ist das leere Wort in der Menge aller Wörter über $\Sigma$ .

$\varepsilon ^{R}=\varepsilon$

Das leere Wort ist identisch mit seiner Spiegelung und damit ein Palindrom.

Weitere Merkmale bei speziellen Anwendungen

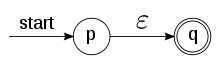
Ein Automat, der das leere Wort unter Verwendung einer $\varepsilon$ -Transition akzeptiert

Die $\varepsilon$ -Übergänge in nichtdeterministischen endlichen Automaten sind Tupel $(q_{1},\varepsilon ,q_{2})$ aus der Übergangsrelation $\Delta$ mit Zuständen $q_{1},q_{2}$ . Ein solcher Übergang bedeutet, dass der Automat seinen Zustand von $q_{1}$ nach $q_{2}$ ändern kann, ohne dass ein Zeichen gelesen wird. $\varepsilon$ -Übergänge sind damit einer der Gründe für Nichtdeterminismus. Sie werden im Graphen als Kanten kenntlich gemacht, die mit einem $\varepsilon$ beschriftet sind.

Auch bei Kellerautomaten sind $\varepsilon$ -Übergänge möglich und bedeuten, dass durch jene Zustandswechsel das Eingabewort nicht abgearbeitet wird. Wird beim Lesen des Kellerinhalts bei einem Übergang das oberste Symbol durch das leere Wort ersetzt, wird es damit aus dem Keller entfernt. Schließlich symbolisiert das leere Wort den leeren Keller, der eines von zwei möglichen Akzeptanzkriterien bei Kellerautomaten ist.

Literatur

John E. Hopcroft, Jeffrey D. Ullman: Einführung in die Automatentheorie, Formale Sprachen und Komplexitätstheorie. 2. Auflage. Pearson Studium, Reading 2002, ISBN 3-8273-7020-5

Basierend auf einem Artikel in:

Wikipedia.de