
Atomorbital

Obere Reihe: Darstellung der Wahrscheinlichkeitsdichten
Untere Reihe: Darstellung von Isoflächen von
Ein Atomorbital ist in den quantenmechanischen
Modellen der Atome
die räumliche Wellenfunktion
eines einzelnen Elektrons
in einem quantenmechanischen
Zustand, meist in einem stationären Zustand. SeinFormelzeichen ist meist
(kleines Phi) oder
(kleines Psi).
Das Betragsquadrat
beschreibt als Dichtefunktion
die räumliche Verteilung der Aufenthaltswahrscheinlichkeit,
mit der das Elektron am Ort
gefunden werden kann (bornsche
Wahrscheinlichkeitsinterpretation der Quantenmechanik). Zusammen mit der
Angabe, ob der Spin zu einer festen Achse oder
zum Bahndrehimpuls
des Elektrons parallel oder antiparallel ausgerichtet ist, beschreibt ein
Orbital den Elektronenzustand vollständig.
In den älteren Atommodellen nach Niels Bohr (Bohrsches Atommodell, 1913) und Arnold Sommerfeld (Bohr-Sommerfeldsches Atommodell, 1916) beschreibt ein Orbital eine genaue, durch die Quantisierungsregeln ausgewählte Elektronenbahn. Diese Vorstellung wurde in der Quantenmechanik zugunsten einer diffusen Verteilung der Aufenthaltswahrscheinlichkeit des Elektrons aufgegeben. Das quantenmechanische Atomorbital erstreckt sich für gebundene Elektronen vom Atomkern im Zentrum nach außen bis ins Unendliche, wo die Aufenthaltswahrscheinlichkeit asymptotisch gegen null geht. Der wahrscheinlichste Abstand vom Atomkern ist für das innerste Orbital gleich dem Radius der 1. bohrschen Kreisbahn.
Anschaulich stellt man ein Orbital gewöhnlich durch die Oberfläche des kleinstmöglichen Volumens dar, in dessen Inneren sich das Elektron mit großer (z.B. 90%iger) Wahrscheinlichkeit aufhält (s. Abbildung). Man erhält damit Körper, die ungefähr der Größe und Form der Atome entsprechen, wie sie sich in chemischen Molekülen, kondensierter Materie und der kinetischen Gastheorie bemerkbar machen.
Die gebräuchlichsten Atomorbitale sind die, die sich für das einzige Elektron
des Wasserstoffatoms als Lösungen der Schrödingergleichung
des Wasserstoffproblems
ergeben und 1926 erstmals veröffentlicht wurden. Sie haben verschiedene Formen,
die mit
bezeichnet werden, wobei der untere Index aus der Hauptquantenzahl
der Bahndrehimpulsquantenzahl
und der magnetischen Quantenzahl
besteht.
Im Orbitalmodell für Atome mit mehreren Elektronen nimmt man an, dass die Elektronen sich unter Berücksichtigung des Pauli-Prinzips auf die Orbitale verteilen. Ein solcher Zustand heißt Elektronenkonfiguration und stellt oft eine brauchbare Näherung für die Struktur der Atomhülle dar, obwohl diese durch zusätzliche Elektronenkorrelationen noch komplizierter ist.
Zur Beschreibung von Elektronen in Molekülen werden Molekülorbitale als Linearkombination von Atomorbitalen gebildet. Elektronen in Festkörpern werden durch Orbitale beschrieben, die die Form von Blochwellenfunktionen haben.
In diesem Artikel wird nur auf gebundene Elektronen in Atomen eingegangen. Eine Vereinfachung des Orbitalmodells ist das Schalenmodell.
Darstellung
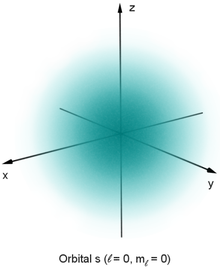
Da die vollständige graphische Darstellung einer Wellenfunktion
vier Dimensionen benötigte (bzw. fünf Dimensionen, falls
),
ist eine vollständige Darstellung im Dreidimensionalen nicht direkt
möglich (aber zum Beispiel unter Zuhilfenahme einer Farbcodierung wie unten in
der Tabelle). Wie vom Wasserstoffatom bekannt ist, haben die Eigenfunktionen
der stationären
Schrödingergleichung
einen Radialanteil
und einen Winkelanteil
:
Diese Anteile können getrennt gezeichnet werden. Häufig zeigen Bilder von
Orbitalen jedoch eine Darstellung der Wahrscheinlichkeitsdichte
(und damit indirekt der Orbitale
).
Besonders einleuchtend könnte die Wahrscheinlichkeitsdichte als Punktwolke visualisiert
werden: Ist die Wahrscheinlichkeitsdichte groß, so werden viele Punkte
gezeichnet; ist die Wahrscheinlichkeitsdichte klein, werden wenige Punkte
gezeichnet. Da die Wahrscheinlichkeitsdichte jedoch an fast allen Punkten
(ausgenommen der Knotenpunkte der Wellenfunktion) im Raum ungleich null ist,
kann ein Orbital auf diese Weise dennoch nicht völlig dargestellt werden –
da man ja bis ins Unendliche weiterhin Punkte zeichnen müsste. Stattdessen geht
man dazu über, Isoflächen
gleicher Wahrscheinlichkeitsdichte zu zeichnen, die implizit durch
definiert sind. Durch Abtasten verschiedener Winkel
erfährt man etwas über die Form der Isofläche und somit etwas über die „Form des
Orbitals“. Die Form des Orbitals wird durch eine Kugelflächenfunktion
vorgegeben. Häufig wird die Konstante so gewählt, dass die Wahrscheinlichkeit,
das Elektron in dem von der Isofläche umschlossenen Raum zu finden, 90 %
beträgt.
Nicht selten wird bei der Darstellung einer Isofläche von
die Fläche entsprechend dem Argument
von
koloriert (wie in dem Bild des p-Orbitals).
Eine einfache Art der schematischen Darstellung der Besetzung von Atomorbitalen ist die Pauling-Schreibweise.
Klassifikation
Atomorbitale können durch drei Quantenzahlen
festgelegt werden und bieten dann Platz für zwei Elektronen mit
entgegengesetztem Spin. Alternativ können
Atomorbitale durch vier Quantenzahlen
festgelegt werden und bieten dann Platz für nur jeweils ein Elektron.
Hauptquantenzahl n: Schale
Die Hauptquantenzahl
bezeichnet die Schale
(Bezeichnung auch K-Schale, L-Schale, M-Schale, …), zu der das Orbital
gehört. Im bohrschen Atommodell gibt
das Energieniveau an,
beginnend mit dem tiefsten, dem Grundzustand
Je größer ,
desto geringer die Bindungsenergie
des Elektrons und damit desto größer die Wahrscheinlichkeit, das Elektron weiter
entfernt vom Atomkern zu finden. Das gilt auch für Atome mit mehreren
Elektronen. Bei Wechselwirkungen zwischen Atomen, die sich nahe kommen, (wie Stößen von
Gasmolekülen, Raumerfüllung in kondensierter Materie, chemischen Bindungen)
spielen deshalb die Elektronen mit der größten Hauptquantenzahl die wichtigste
Rolle (die Elektronen der Valenzschale).
Die Anzahl der -Orbitale
in einer Schale ergibt sich zu
Unter Berücksichtigung des Pauli-Prinzips
kann die Schale mit maximal
Elektronen besetzt werden, dann ist sie abgeschlossen. Die entsprechenden
Atome gehören zu den Edelgasen.
Neben- oder Bahndrehimpuls-Quantenzahl l
Form
Die Neben- oder Bahndrehimpulsquantenzahl
innerhalb einer Schale beschreibt den Betrag
des Bahndrehimpulses
des Elektrons. Mit der Quantenzahl
zusammen wird damit die winkelabhängige „Form“ des Orbitals festgelegt. Sie ist
für alle Hauptquantenzahlen (beachte
)
dieselbe.
Statt der Ziffern 0, 1, 2 etc. wird die Nebenquantenzahl in der Literatur meist durch die Buchstaben s, p, d, f, g etc. bezeichnet, abgeleitet aus den ursprünglichen Bezeichnungen für die korrespondierenden Spektrallinien; diese konkrete Bedeutung ist seit langem unwesentlich geworden:
 |
 |
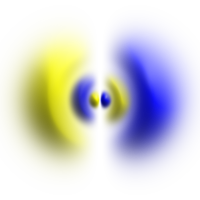 |
| Vereinfachte Form eines p-Orbitals Die Färbung steht für das Vorzeichen der Wellenfunktion. Dargestellt ist eine Isofläche von |
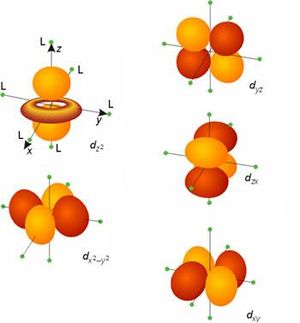
Vereinfachte Formen der verschiedenen d-Orbitale (jeweils |
Form eines 4p-Orbitals Die Färbung steht für das Vorzeichen der Wellenfunktion. |
| Name | ehemalige Bedeutung | Nebenquantenzahl | Form | Anzahl |
|---|---|---|---|---|
| s-Orbital | sharp | kugelsymmetrisch | 1 | |
| p-Orbital | principal | hantelförmig | 3A2 | |
| d-Orbital | diffuse | gekreuzte Doppelhantel | 5 | |
| f-Orbital | fundamental | rosettenförmig | 7 | |
| g-OrbitalA1 | (alphabetische Fortsetzung) | rosettenförmig | 9 | |
| h-OrbitalA1 | (alphabetische Fortsetzung) | rosettenförmig | 11 |
Anmerkungen:
Die Orbitale charakterisieren streng genommen nur die stationären Elektronen-Wellen in Systemen mit nur einem Elektron (wie z.B. Wasserstoffatom H, Heliumion He+, Lithiumion Li2+ usw.). Da die Form der Orbitale auch in Mehrelektronensystemen in etwa erhalten bleibt, reicht ihre Kenntnis aus, um viele qualitative Fragen zur chemischen Bindung und zum Aufbau von Stoffen zu beantworten.
Dabei ist zu beachten, dass die in der Literatur dargestellten Orbitale
zuweilen nicht die Eigenzustände
zur magnetischen Quantenzahl
der z-Komponente des Drehimpulsoperators
sind. Z.B. wird von den p-Orbitalen nur der eine Eigenzustand für den Eigenwert
dargestellt und als pz bezeichnet. Die mit px und
py bezeichneten Orbitale sind jedoch nicht die entsprechenden
Eigenzustände für
sondern sind deren Superpositionen.
Sie sind Eigenzustände zu den Operatoren
bzw.
jeweils zu
die aber nicht mit
kommutieren. Für die Schlussfolgerungen ist das kein Problem, solange die
entsprechenden Wellenfunktionen orthogonal
sind.
Unterschale
Je größer ,
desto größer ist bei festem
die mittlere Entfernung des Elektrons vom Atomkern:
- Bei
ist das Orbital kugelförmig und hat auch bei
also im Kern, eine nichtverschwindende Aufenthaltswahrscheinlichkeit.
- Der Maximalwert
entspricht der bohrschen Kreisbahn, hier konzentriert sich die Aufenthaltswahrscheinlichkeit bei dem im bohrschen Modell berechneten Radius.
Da bei Atomen mit mehreren Elektronen die inneren
Elektronen die anziehende Kernladung
abschirmen,
verringert sich die Bindungsenergie der äußeren Elektronen. Da die mittleren
Kernabstände von der Nebenquantenzahl abhängen, ergeben sich zum gleichen
je nach Nebenquantenzahl verschiedene Energieniveaus innerhalb derselben Schale.
Diese werden auch als Unterschalen der Hauptschale (zu festem
)
bezeichnet.
Die Anzahl der Unterschalen je Schale ist gleich der Hauptquantenzahl :
- Für
gibt es nur die 1s-Schale.
- Für
sind drei Unterschalen
möglich, die mit 3s, 3p, 3d bezeichnet werden.
Pro Unterschale gibt es
Orbitale (jeweils mit anderer Magnetquantenzahl
,
s. folgenden Abschnitt), was auf insgesamt
Orbitale pro Schale führt.
Magnetquantenzahl ml: Neigung des Drehimpulsvektors
Die Magnetquantenzahl
gibt die z-Komponente
des Bahndrehimpulsvektors gegenüber einer (frei gewählten) z-Achse an. Das
entspricht anschaulich einem Neigungswinkel
- Bei
liegt der Bahndrehimpuls (etwa) parallel zur Achse,
- bei
(etwa) antiparallel.
Dass bei gegebenem
genau
verschiedene Werte möglich sind, wird als Richtungsquantelung
bezeichnet.
Wenn kein äußeres Feld anliegt, haben die
einzelnen Orbitale einer Unterschale gleiche Energie. Dagegen spaltet im Magnetfeld die Energie
innerhalb der Unterschale in
äquidistante Werte auf (Zeeman-Effekt),
d.h., jedes einzelne Orbital entspricht dann einem separaten
Energieniveau.
Magnetische Spinquantenzahl ms
Bei den leichteren Atomen braucht man den Elektronenspin
nur in der Form zu berücksichtigen, dass jedes Orbital
von genau einem Elektronenpaar
besetzt werden kann, dessen zwei Elektronen nach dem Pauli-Prinzip
entgegengesetzte magnetische Spinquantenzahlen aufweisen (
).
Gesamtdrehimpuls j und magnetische Quantenzahl mj
Zu den schweren Atomen hin wird die Spin-Bahn-Wechselwirkung
stärker. Sie bewirkt die Aufspaltung der Energie einer Unterschale mit
bestimmten
in zwei Unterschalen, je nach Wert des Gesamtdrehimpulses
Die magnetische Quantenzahl
durchläuft
Werte. Jedes dieser Orbitale kann von einem Elektron besetzt werden, sodass die
Gesamtzahl der Plätze gleich bleibt. In der Bezeichnung wird der Wert für
als unterer Index an das Symbol für
angefügt, z.B.
Quantentheorie
Aus der nichtrelativistischen Quantentheorie ergeben sich die Orbitale wie folgt: Die Wechselwirkung zwischen Elektron und Atomkern wird durch das Coulombpotential beschrieben, der Atomkern als fix angenommen. Der Hamiltonoperator für das Ein-Elektron-System ist
mit dem Potential
.
Da der Hamiltonoperator mit dem Drehimpulsoperator kommutiert, bilden
und
ein vollständiges
System kommutierender Observablen. Zu diesen drei Operatoren gibt es also
gemeinsame Eigenzustände, die durch die drei zugehörigen Quantenzahlen
bestimmt sind.
Die Schrödingergleichung
lässt sich in einen radius- und einen winkelabhängigen Teil zerlegen. Die
Eigenfunktionen
sind das Produkt aus einer Kugelflächenfunktion
(Eigenfunktion des Drehimpulsoperators) und einer radialen Funktion
Diese sind bis
in der folgenden Tabelle normiert dargestellt. Dabei bezeichnen
den Bohrschen
Radius und
die Kernladungszahl.
Die in der folgenden Tabelle dargestellten Orbitale sind alle um die z-Achse
ausgerichtet, weil es sich um Eigenfunktionen des -Operators
handelt. Für Ausrichtung eines Orbitals mit gegebenem Bahndrehimpuls
in eine beliebige andere Richtung muss man Linearkombinationen der
Wellenfunktionen zu den verschiedenen
bilden. Die grafische Darstellung zeigt ein Volumen, auf dessen Oberfläche die
Aufenthaltswahrscheinlichkeitsdichte
konstant ist. Die Farben kodieren die komplexe Phase der Wellenfunktion.
| Orbital | Wellenfunktion des Orbitals | Form des Orbitals | |||
|---|---|---|---|---|---|
| 1s | 1 | 0 | 0 | ||
| 2s | 2 | 0 | 0 |  | |
| 2p0 | 2 | 1 | 0 |  | |
| 2p-1/+1 | 2 | 1 | ±1 |   | |
| 3s | 3 | 0 | 0 |  | |
| 3p0 | 3 | 1 | 0 |  | |
| 3p-1/+1 | 3 | 1 | ±1 |  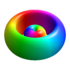 | |
| 3d0 | 3 | 2 | 0 |  | |
| 3d-1/+1 | 3 | 2 | ±1 |   | |
| 3d-2/+2 | 3 | 2 | ±2 |   | |
Natürliches Orbital
Ein natürliches Orbital ist ein Orbital, das sich nicht als Eigenfunktion eines Hamiltonoperators ergibt, sondern als Eigenfunktion eines Einelektronen-Dichteoperators. Dieser wird aus einem vorgegebenen Vielteilchenzustand gewonnen, der beispielsweise auch Elektronenkorrelationen enthalten kann und damit über den Rahmen eines Einzelteilchenmodells hinausgeht. Die mit den natürlichen Orbitalen gebildete Elektronenkonfiguration ergibt die beste Annäherung an den anfangs gegebenen Vielteilchenzustand, die mit einem Einzelteilchenmodell möglich ist.
Zeitabhängigkeit
Werden Orbitale als Eigenfunktionen eines Operators definiert, der zu einer
Energie korrespondiert, dann sind diese Orbitale im Rahmen des gewählten Modells
stationär. Beispiele hierfür sind die Hartree-Fock-Orbitale
als Eigenfunktionen des Fockoperators
und die Kohn-Sham-Orbitale,
die Eigenfunktionen des Kohn-Sham-Hamilton-Operators sind. Im Gegensatz dazu
sind die sogenannten natürlichen Orbitale, als Eigenfunktionen des
reduzierten Einelektronen-Dichteoperators,
nicht stationär.
Hybridisierung
Einige Symmetrien von chemischen Bindungen scheinen den charakteristischen Formen der Orbitale zu widersprechen. Diese Bindungen werden durch die Bildung von Hybrid-Orbitalen verständlich, die sich bei Anwesenheit von Elektronen mit verschiedenem Bahndrehimpuls bilden können, wenn sie energetisch nahezu gleichwertig sind (siehe oben).
Mehr-Elektronen-Wellenfunktionen
Die Interpretation von Orbitalen als Wellenfunktionen je eines Elektrons ist nur bei Einzelelektronensystemen eindeutig möglich. Eine Wellenfunktion für N Elektronen kann dann konstruiert werden, indem man N Orbitale in eine Slater-Determinante einsetzt. Dies garantiert die für Fermionen notwendige Antisymmetrie der gesamten Wellenfunktion, kann aber darüber hinaus gehende Elektronenkorrelationen nicht darstellen. Um auch die Elektron-Elektron-Wechselwirkung näherungsweise zu berücksichtigen, können die Orbitale durch Hartree-Fock-, Kohn-Sham-Rechnungen (siehe: Dichtefunktionaltheorie in der Quantenphysik) oder MCSCF-Rechnungen (MCSCF: Multiconfiguration Self Consistent Field) bestimmt werden. Doch stets bleibt gültig, dass anders gewählte Orbitale, wenn sie linear unabhängige Linearkombinationen der ursprünglichen sind, mathematisch die gleiche Slater-Determinante ergeben, sodass man aus einer gegebenen Mehrteilchen-Wellenfunktion nicht eindeutig zurückschließen kann, welches die einzelnen besetzten Orbitale sind.
Literatur
- Wolfgang Demtröder: Atome, Moleküle und Festkörper. 3. Auflage. Springer, 2002, ISBN 3-540-21473-9.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.10. 2021