Bindungsenergie
Bindungsenergie muss aufgebracht werden, um ein gebundenes System aus zwei oder mehr
Bestandteilen (beispielsweise ein Molekül, ein Atom, einen
Atomkern oder auch einen ganzen Himmelskörper oder Galaxienhaufen), die durch Anziehungskräfte zusammengehalten werden,
in seine Bestandteile zu zerlegen. Eine ebenso große Energie wird freigesetzt, wenn sich das gebundene System aus den Einzelteilen bildet. Manchmal wird unter
Bindungsenergie nicht diese Energiemenge selbst, sondern die Änderung des Energieinhalts des Systems verstanden, wenn seine Teile sich miteinander verbinden;
dann hat sie den gleichen Betrag, ist aber negativ. So ist z. B. die in der Chemie gebräuchliche Reaktionsenthalpie
negativ, wenn der Energieinhalt des Systems bei der Reaktion abnimmt, weil Energie frei wird.
Die Bezeichnung Bindungsenergie ist ein gängiger Fachausdruck, aber sprachlich etwas unglücklich gewählt. Sie führt – besonders mit einem nachfolgenden Genitiv, wie z. B. Bindungsenergie „des Uran-Atomkerns“ oder „des ATP-Moleküls“ – leicht zu dem Missverständnis, es handele sich um einen Energiebetrag, der in dem gebundenen System vorhanden ist und aus ihm freigesetzt werden kann. Richtig ist, wie oben gesagt, das Gegenteil: Die Bindungsenergie ist bereits bei der Bildung des gebundenen Systems freigesetzt und abgegeben worden, ist also nun nicht mehr verfügbar.
Veranschaulichung
Wenn beispielsweise der Abstand zweier Dauermagnete hinreichend gering ist, ziehen sie einander an und bewegen sich aufeinander zu. Augenblicke vor dem Zusammenstoß besitzen beide Magnete ihre höchste kinetische Energie, welche dann in Schallenergie und Wärme umgewandelt, also „freigesetzt“ wird. Um die Magnete wieder voneinander zu trennen, muss die Bindungsenergie aufgebracht werden. Sie stimmt vom Betrag her mit der insgesamt vorher freigesetzten Energie überein.
Chemie
In der Chemie wird der Begriff Bindungsenergie für die Bildung von Molekülen aufgrund einer kovalenten Bindung durch Kräfte kurzer Reichweite gebraucht. Bei der Bildung von Ionenkristallen aufgrund der langreichweitigen elektrostatischen Anziehung wird die molare Bindungsenergie als Gitterenergie und Gitterenthalpie bezeichnet.
Bindungsenergien zwischen Atomen liegen bei Molekülen zwischen 200 und 700 kJ·mol−1 (2 bis 7 eV pro Bindung). Besonders geringe Bindungsenergien beobachtet man bei Wasserstoffbrückenbindungen. Sie sind mit nur 17 bis 167 kJ/mol[1] (0,18 bis 1,7 eV pro Bindung) deutlich schwächer als die Bindungskraft innerhalb eines Moleküls.
Atomphysik
In der Atomphysik wird als Bindungsenergie die Energie bezeichnet, die zum Zerlegen eines Atoms/Ions in ein (anderes) Ion und ein Elektron nötig ist. Sie kommt durch die elektrische Anziehung zwischen Elektron und Atomkern zustande. Beim Einfangen eines Elektrons wird der gleiche Energiebetrag frei. Chemiker bevorzugen anstelle von Bindungsenergie oft den Terminus Ionisierungsenergie.
Besonders geringe Bindungsenergien besitzen die Valenzelektronen der ersten Hauptgruppe, von 13,6 eV beim Wasserstoffatom über 5,14 eV für Natrium bis 3,9 eV für Caesium. Je höher geladen ein Ion wird, desto höher wird auch die Bindungsenergie der verbliebenen Elektronen. So betragen die zweite und dritte Ionisierungsenergie bei Natrium schon 47 beziehungsweise 72 eV.[2]
Um ein Elektron aus einem ungeladenen Festkörper zu entfernen, muss Energie aufgewendet werden, die als Austrittsarbeit bezeichnet wird. Sie ist oft erheblich geringer als die Bindungsenergie im isolierten Atom und beträgt z. B. beim Caesium nur 2,14 eV. Ihr Wert lässt sich durch den Schottky-Effekt verringern. Die Austrittsarbeit ist z. B. beim Edison-Richardson-Effekt, Sekundärelektronenvervielfacher, Sekundärelektronenmikroskop und photoelektrischen Effekt von Bedeutung.
Auch bei einem gleichrichtenden Metall-Halbleiter-Übergang wie in der Schottky-Diode müssen Elektronen die Schottky-Barriere überwinden, diese liegt meist zwischen 0,5 und 0,9 eV. Die Bandlücke im Bändermodell eines Halbleiters entspricht der Bindungsenergie eines Elektrons im Valenzband.
Manchmal ist mit Bindungsenergie diejenige des gesamten Atoms (also nicht nur die eines einzelnen Elektrons) gemeint. Wir bezeichnen mit
die Bindungsenergie aller Elektronen der Hülle eines Atoms. Sie ist gleich
der Differenz der Energieäquivalente der Summe aller Massen ohne Bindung und des
Energieäquivalents der Masse des neutralen Atoms
.
Dabei bedeuten
die Kernmasse des Atoms,
seine Ordnungszahl,
die Masse eines Elektrons,
die Masse des neutralen Atoms,
die Lichtgeschwindigkeit.
Die gesamte Bindungsenergie
der Elektronenhülle kann nicht leicht im Experiment gemessen werden. Man ist stattdessen weitgehend auf
theoretische Abschätzungen[3]
angewiesen. Für Uran-Isotope 92U, also
, zum Beispiel ergibt sich aus Rechnungen eine totale elektronische Bindungsenergie von etwa 760 keV.[4] Zum Vergleich sei daran erinnert, dass das Energieäquivalent der Masse eines Elektrons 511 keV
beträgt.
Kernphysik
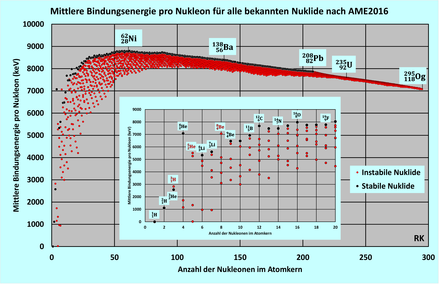
In der Kernphysik bedeutet Bindungsenergie meist die gesamte Bindungsenergie. Das ist die Energiemenge, die aufgewandt werden muss, um den Atomkern vollständig in seine Nukleonen zu zerlegen.[5] Die Bindungsenergie kann sich auch auf ein einzelnes Nukleon beziehen und wird dann genauer als Ablöse- oder Abtrennarbeit des betreffenden Teilchens bezeichnet. Umgekehrt wird eine ebenso große Energie frei, wenn das Teilchen wieder gebunden wird bzw. sämtliche Nukleonen sich zu einem Kern vereinigen.
Die Bindung kommt durch die anziehende Kraft der starken Wechselwirkung zwischen benachbarten Nukleonen zustande. Diese überwiegt die gegenseitige Coulomb-Abstoßung der elektrisch positiv geladenen Protonen im Kern. Die maximale Bindungsenergie pro Nukleon wird bei Nickel-62[6] erreicht. Die geringere Bindungsenergie pro Nukleon außerhalb dieses Maximums ist anschaulich verständlich:
- Leichtere Kerne haben einen größeren Bruchteil ihrer Nukleonen an der Oberfläche, wo sie weniger bindende Nachbarn haben.
- Bei schwereren Kernen beginnt die abstoßende Coulombkraft aller Protonen mit ihrer langen Reichweite die starke, aber kurzreichweitige anziehende Kraft der nächsten Nachbarn zu überwiegen.
Daher kann im Gebiet der leichten Kerne durch Kernverschmelzung (Kernfusion), im Gebiet der schweren Kerne aber durch Kernspaltung technisch nutzbare Energie gewonnen werden.
Der generelle Verlauf der Bindungsenergie von Atomkernen kann im Tröpfchenmodell mit der Bethe-Weizsäcker-Formel modelliert werden. Zur Erklärung der kleinen Abweichungen (Zacken in der Graphik) ist das Schalenmodell heranzuziehen.
Die Bindung ist wegen der Äquivalenz von Masse und Energie mit einem
Massendefekt verbunden: Der gebundene Kern hat zwischen 0,1 %
(Deuteron) und 0,9 % (Ni-62) weniger Masse als alle seine Nukleonen zusammengenommen. Aus einer genauen Bestimmung
der Masse
eines Atoms lässt sich daher die Bindungsenergie
des Kerns ableiten:
Dabei ist
die Masse des Atoms,
s eine Massenzahl,
seine Ordnungszahl,
die Masse eines freien Protons,
die Masse eines Elektrons,
die Masse eines freien Neutrons,
die Lichtgeschwindigkeit.
Die Bindungsenergie kurzlebiger Kerne lässt sich beispielsweise über die Messung der Energien ihrer Zerfallsprodukte bestimmen, jedenfalls relativ zu deren Bindungsenergien.
Gravitation
Die gravitative Bindungsenergie ist diejenige Energie, die benötigt wird, um einen durch Gravitation zusammengehaltenen Körper (z. B. die Erde) in sehr viele winzige Bestandteile zu zerlegen und diese unendlich weit voneinander zu entfernen. Umgekehrt wird die gleiche Energiemenge freigesetzt, wenn sich diese Bestandteile zu einem gravitativ gebundenen Körper zusammenfügen. Dies geschieht beim Kollaps einer Gaswolke zu einem kompakteren Himmelskörper, etwa einem Stern (Jeans-Kriterium), und führt zu einer Erwärmung der Wolke.
Bindungsenergie einer homogenen Kugel
Die Bindungsenergie
ergibt sich aus der Überlegung, die Kugel schichtweise aufzubauen, indem aus dem Unendlichen kommende Materie angefügt wird. Hat die Kugel einen Radius
erreicht, ist ihr Volumen
und bei konstanter Dichte
ihre Masse
.
Sie erzeugt im Außenraum
() das Gravitationspotential
.
Die nächste Schicht der Dicke
bedeckt die Oberfläche
und hat (bei gleicher Dichte) die Masse
.
Die dabei freiwerdende Energie ist
.
Baut man so Schicht für Schicht eine Kugel mit Radius
und Masse
zusammen, so wird insgesamt die folgende Bindungsenergie frei:
Die Bindungsenergie beträgt also
.
Eine homogene Kugel mit Masse und Radius der Erde besäße nach dieser Formel eine gravitative Bindungsenergie von etwa 2,24 · 1032 J. Die Erde ist allerdings keine Kugel homogener Dichte, der Erdkern hat eine fast doppelt so hohe Dichte wie der Erdmantel. Aus der Dichteverteilung im Erdinnern nach dem „Preliminary Reference Earth Model“ (PREM) errechnet sich die Bindungsenergie der Erde daher etwas größer, nämlich zu 2,489 · 1032 J.
Allgemeine Relativitätstheorie
Nach der Allgemeinen Relativitätstheorie berechnet sich die Bindungsenergie im Gravitationspotential mit dem Shapirofaktor σ aus der Ruheenergie m im Nullpotential
Für eine Hohlkugel mit Radius r ergibt sich dann die Eigenbindungsenergie aus der gemessenen Masse M
Weblinks
- "Was ist Bindungsenergie?" aus der Fernseh-Sendereihe
 alpha-Centauri (ARD-Alpha)
(ca. 15 Minuten). Erstmals ausgestrahlt am 12. Mai 2004.
alpha-Centauri (ARD-Alpha)
(ca. 15 Minuten). Erstmals ausgestrahlt am 12. Mai 2004.
Einzelnachweise
- ↑ George A. Jeffrey: An Introduction to Hydrogen Bonding. Oxford University Press, 1997, ISBN 0-19-509549-9.
- ↑
 Eigenschaften von Natriumatomen bei webelements.com.
Eigenschaften von Natriumatomen bei webelements.com.
- ↑
Keh-Ning Huang et al.: Neutral-atom electron binding energies from relaxed-orbital relativistic Hartree-Fock-Slater calculations
2 ≤ Z ≤ 106. In: Atomic Data and Nuclear Data Tables.
Band 18,
Nr. 3, 1976,
S. 243–291,
doi:
 10.1016/0092-640X(76)90027-9.
10.1016/0092-640X(76)90027-9.
- ↑
Georges Audi: A Lecture on the Evaluation of Atomic Masses. 2004, S. 11 (31 S.,
 Hall Sience [PDF]).
Hall Sience [PDF]).
- ↑ Wolfgang Demtröder: Experimentalphysik 4: Kern-, Teilchen- und Astrophysik, Springer DE 2009,
ISBN 3-642-01597-2, S. 26;
 eingeschränkte Vorschau in der Google-Buchsuche
eingeschränkte Vorschau in der Google-Buchsuche
- ↑ M. P. Fewell: The atomic nuclide with the highest
mean binding energy. In: American Journal of Physics.
Band 63,
Nr. 7, 1995,
S. 653–658,
doi:
 10.1119/1.17828,
bibcode:
10.1119/1.17828,
bibcode:  1995AmJPh..63..653F (englisch).
Darin wird auch dargestellt, wie die falsche, aber immer noch verbreitete Zuschreibung der festesten Bindung zu Eisen-56 entstanden sein könnte. Tatsächlich ist Ni-62 pro
Nukleon um 0,04 % fester gebunden.
1995AmJPh..63..653F (englisch).
Darin wird auch dargestellt, wie die falsche, aber immer noch verbreitete Zuschreibung der festesten Bindung zu Eisen-56 entstanden sein könnte. Tatsächlich ist Ni-62 pro
Nukleon um 0,04 % fester gebunden.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.03. 2025