Embacher-Methode

Die Methode Embacher ist ein Verfahren der geodätischen Astronomie zur genauen Azimut- und Breitenbestimmung.

Sie wurde in den 1950er Jahren von Wilhelm Embacher (TH Wien und Universität Innsbruck) entwickelt und hat die Besonderheit, kein genaues Zeitsystem zu erfordern.

Es werden jeweils polnahe Sternpaare im maximalen Azimut beobachtet, d. h. im Nordwest- und Nordostquadrant. In dieser Stellung (Größte Digression) bewegen sie sich genau lotrecht nach unten oder oben. Die gemessene Azimutdifferenz ist eine Funktion von geografischer Breite und Deklination und dient der Breitenbestimmung, während die vertikalen Sterndurchgänge selbst das Azimut des anschließend einzumessenden terrestrischen Zieles ergeben.

Berechnung

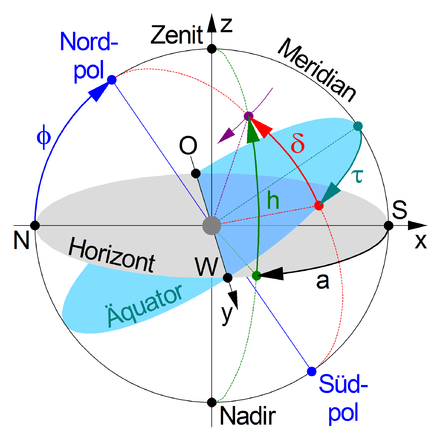
Himmelskoordinaten in astronomischen Koordinatensystemen: Das zu betrachtende sphärische Dreieck hat auf der Nordhalbkugel die Eckpunkte Nordpol (blau), Zenit (schwarz) und Stern (violett). $a$ ist der Azimut im Horizontsystem, vom Meridian aus gemessen (schwarz); im Äquatorsystem ist $\delta$ die Deklination (rot), vom Himmelsäquator aus gemessen, sowie $\tau$ der Stundenwinkel (cyan), ebenfalls vom Meridian aus gemessen. Die geografische Breite des Beobachtungsortes ist identisch mit der Polhöhe $\phi$ .

Da das astronomische Dreieck (Pol-Zenit-Stern) für den Moment der größten Digression rechtwinklig wird (mit dem rechten Winkel am Stern), vereinfachen sich die sphärischen Formeln wesentlich; Sinus- bzw. Tangenssatz reduzieren sich auf:

$\sin a={\frac {\cos \delta }{\cos \phi }}$ (im Osten positiv, im Westen negativ)

$\cos \tau ={\frac {\tan \phi }{\tan \delta }}$ (Stundenwinkel im vierten bzw. ersten Quadranten)

mit

dem Azimut $a$ des Sterns
seiner Deklination $\delta$
seinem Stundenwinkel $\tau$
der geografische Breite $\phi$ des Standorts.

Misst man daher die Azimutdifferenz $\Delta a=a_{2}-a_{1}$ zweier Sterne, die im Osten bzw. Westen innerhalb weniger Minuten digressieren, so ergibt sich die Breite $\phi$ durch eine Umformung der ersten Formel (mittels $\Delta _{1}$ und $\Delta _{2}$ ), woraus man die beiden Sternazimute $a_{1}$ und $a_{2}$ berechnen kann.

Damit ist am Messinstrument die genaue Orientierung des Horizontalkreises bekannt (Sternazimut minus Kreislesung), sodass man das vor oder nach den Sternen gemessene terrestrische Ziel um diesen Betrag korrigieren kann, was dessen gesuchtes Azimut ergibt.

Literatur

Wilhelm Embacher: Neue Vorschläge zur geografischen Ortsbestimmung, Österreichische Zeitschrift für Vermessungswesen, Jahrgang.1952, Seiten 3 bis 13, 50-58 und 82 bis 88, Wien, 1952.

Basierend auf einem Artikel in:

Wikipedia.de