Größte Digression

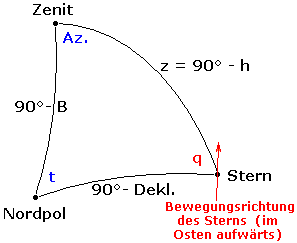
Astronomisches Dreieck mit den 3 Seiten (Kobreite 90° − B, Poldistanz 90° − Dekl., Zenitdistanz z) und den 3 Winkeln (Azimut Az, Stundenwinkel t, parallaktischer Winkel q). In die größte Digression kommt der Stern etwa eine Stunde später, wenn seine Bewegungsrichtung genau zum Zenit weist.

Als Größte Digression werden jene zwei Stellen bzw. Zeitpunkte der täglichen Sternbewegung bezeichnet, bei denen sich ein Gestirn genau senkrecht nach oben (östliche Digression) bzw. senkrecht nach unten bewegt (westliche Digression). Dabei bedeutet Digression die momentane, auf den Horizont bezogene Winkeldifferenz eines Gestirns zum örtlichen Meridian oder einer entsprechenden Mire>. Auf der täglichen Sternbahn ist dieser Winkel dann am größten, wenn der Stern sich senkrecht zum Horizont (also parallel zum Meridian) bewegt.

Relevant ist der Sachverhalt nur bei Zirkumpolarsternen.

Grundlagen

In Moment der genau senkrechten Bewegung – der allerdings im Messfernrohr einige Sekunden und freiäugig einige Minuten dauert – beträgt der parallaktische Winkel q (siehe Bild) genau 90° bzw. −90°, und das Gestirn erreicht sein größtes östliches bzw. westliches Azimut, also den größten Winkelabstand (Digression) vom Nordpunkt.

Diese zwei Stellungen treten nur bei Zirkumpolarsternen auf, deren obere Kulmination zwischen Pol und Zenit liegt:

Auf der Nordhalbkugel der Erde muss daher die Deklination δ des Sterns größer sein als die geografische Breite B des Beobachtungsortes, z. B. für München oder Wien δ > +48°.
Auf der Südhalbkugel muss die Deklination kleiner sein als B (also südlicher), z. B. für Kapstadt δ < -34°.

Alle anderen (südlicheren) Sterne des Nordhimmels bewegen sich monoton nach rechts, d. h. immer im Sinne Ost → Süd → West. Sieht man vom Sternauf- bzw. -untergang ab, so nimmt ihr Azimut von 0° (untere Kulmination tief im Norden) über 90° (Osten, Erster Vertikal) aufsteigend bis 180° (Süden, obere Kulmination) dauernd zu, und dann absinkend über 270° (Westen) wieder bis 360° (= 0°) im Norden.

Berechnung

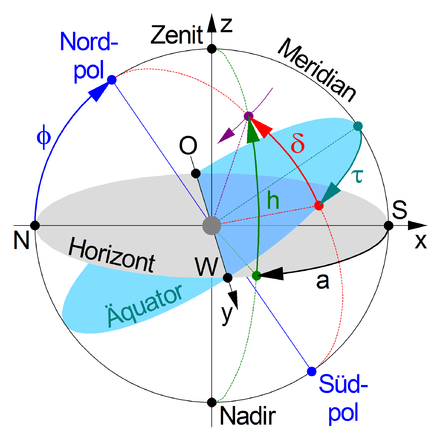
Himmelskoordinaten in astronomischen Koordinatensystemen: Das zu betrachtende sphärische Dreieck hat auf der Nordhalbkugel die Eckpunkte Nordpol (blau). Zenit (schwarz) und Stern (violett). $a$ ist der Azimut im Horizontalsystem vom Meridian aus gemessen (schwarz) und im Äquatorsystem ist $\delta$ die Deklination (rot) von der Äquatorialebene aus gemessen sowie $\tau$ der Stundenwinkel (cyan) ebenfalls vom Meridian aus gemessen. Die geographische Breite des Beobachtungsortes ist identisch mit der Polhöhe $\phi$ .

Weil das astronomische Dreieck (Pol-Zenit-Stern) für den Moment der größten Digression rechtwinklig wird (mit dem rechten Winkel am Stern), vereinfachen sich die sphärischen Formeln wesentlich; Sinus- bzw. Tangenssatz reduzieren sich auf:

$\sin a={\frac {\cos \delta }{\cos \phi }}$ (im Osten positiv, im Westen negativ)

$\cos \tau ={\frac {\tan \phi }{\tan \delta }}$ (Stundenwinkel im vierten bzw. ersten Quadranten)

mit

dem Azimut $a$ des Sterns
seiner Deklination $\delta$
seinem Stundenwinkel $\tau$
der geografische Breite $\phi$ des Standorts.

Anwendung in der Geodäsie

Die erste Formel lässt sich nach Wilhelm Embacher für präzise Breiten- und Azimutmessungen nützen, wenn man Sternpaare im Nordosten und -westen kombiniert:
Denn die größte Digression ist beobachtungstechnisch interessant und von Vorteil, weil der senkrechte Sterndurchgang eine besonders genaue Einstellung am Vertikalfaden eines Theodolits oder Passageninstruments erlaubt. Dabei lässt sich auch die Luftunruhe visuell gut herausmitteln, ferner benötigt man keine genaue Uhrzeit (Zeitfehler). Diese drei Vorteile macht sich z. B. die Embacher-Methode der Azimut- und Breitenbestimmung zunutze.

Siehe auch

Größte Elongation

Literatur

Karl Ramsayer: Geodätische Astronomie. Band IIa. In: Handbuch der Vermessungskunde. J.B. Metzler-Verlag, Stuttgart 1969

Basierend auf einem Artikel in:

Wikipedia.de