Sinussatz

In der Trigonometrie stellt der Sinussatz eine Beziehung zwischen den Winkeln eines allgemeinen Dreiecks und den gegenüberliegenden Seiten her.

Aussagen des Sinussatzes

Sinussatz

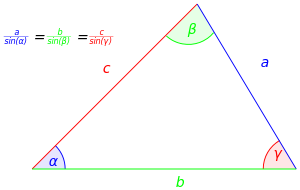
Sind a, b und c die Seiten eines Dreiecks mit Flächeninhalt A, α, β und γ die jeweils gegenüber liegenden Winkel und R der Radius des Umkreises, dann gilt mit der Sinusfunktion $\sin$ :

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}={\frac {abc}{2A}}=2R$

Wenn mit Hilfe des Sinussatzes Winkel im Dreieck errechnet werden sollen, muss darauf geachtet werden, dass es im Intervall [0°;180°] im Allgemeinen zwei verschiedene Winkel mit demselben Sinuswert gibt; diese Zweideutigkeit entspricht der des Kongruenzsatzes SSW.

Zum Zusammenhang mit den Kongruenzsätzen und zur Systematik der Dreiecksberechnung siehe den Artikel zum Kosinussatz.

In der sphärischen Trigonometrie gibt es einen entsprechenden Satz, der ebenfalls als Sinussatz bezeichnet wird.

Geschichte

Er wurde von Abu Nasr Mansur (persischer Mathematiker und Astronom; um 960 bis 1036 n. Chr.) erstmals bewiesen. Der erste Beweis wird in einigen wenigen Quellen Al-Battani, in anderen Abu Mahmud al-Chudschandi zugeschrieben.

Beweis

Dreieck mit Höhe $h_{c}$

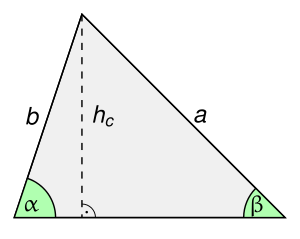
Die eingezeichnete Höhe $h_{c}$ zerlegt das Dreieck in zwei rechtwinklige Teildreiecke, in denen man den Sinus von $\alpha$ und $\beta$ jeweils als Quotient von Gegenkathete und Hypotenuse ausdrücken kann:

$\sin \alpha ={\frac {h_{c}}{b}}$

$\sin \beta ={\frac {h_{c}}{a}}$

Auflösen nach $h_{c}$ ergibt:

$h_{c}=b\cdot \sin \alpha$

$h_{c}=a\cdot \sin \beta$

Durch Gleichsetzen erhält man demnach

$a\cdot \sin \beta =b\cdot \sin \alpha$ .

Dividiert man nun durch $\sin \alpha \cdot \sin \beta$ , so erhält man den ersten Teil der Behauptung:

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}$

Die Gleichheit mit ${\tfrac {c}{\sin \gamma }}$ ergibt sich entsprechend durch Benutzung der Höhe $h_{a}$ oder $h_{b}$ . Um auch noch die Übereinstimmung mit zu zeigen, die streng genommen nicht zum Sinussatz gehört, benötigt man den bekannten Satz über Peripheriewinkel (Umfangswinkel) oder den Kosinussatz zusammen mit dem Peripherie-/Zentriwinkelsatz.

Anwendungsbeispiel

Die folgenden Zahlenwerte sind grobe Näherungen. In einem Dreieck ABC sind folgende Seiten- und Winkelgrößen bekannt (Bezeichnungen wie üblich):

$a=5{,}4\,\mathrm {cm} ;\ b=3{,}8\,\mathrm {cm} ;\ \alpha =73^{\circ }.$

Gesucht sind die Größen der restlichen Seiten und Winkel. Als erstes verwendet man den Sinussatz zur Berechnung von $\beta$ . Danach gilt

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }},$

was sich umformen lässt zu

$\sin \beta ={\frac {b\cdot \sin \alpha }{a}}={\frac {3{,}8\,\mathrm {cm} \cdot \sin 73^{\circ }}{5{,}4\,\mathrm {cm} }}\approx 0{,}67,$

woraus sich mit Hilfe des Arkussinus, der Umkehrfunktion des Sinus,

$\beta \approx \arcsin(0{,}67)\approx 42^{\circ }$

errechnen lässt.

Eigentlich gibt es noch einen zweiten Winkel mit demselben Sinuswert, nämlich $\beta '=180^{\circ }-\beta \approx 138^{\circ }$ . Dieser kommt als Lösung aber nicht in Betracht, da sonst die Winkelsumme des Dreiecks die vorgeschriebenen $180^{\circ }$ überschreiten würde.

$\gamma$ erhält man nun mit Hilfe der Winkelsumme

$\gamma =180^{\circ }-\alpha -\beta \approx 180^{\circ }-73^{\circ }-42^{\circ }=65^{\circ }$ .

Die Seitenlänge soll wieder mit dem Sinussatz ermittelt werden. (Auch der Kosinussatz wäre hier möglich.) Es gilt

${\frac {a}{\sin \alpha }}={\frac {c}{\sin \gamma }}.$

Durch Umformung gelangt man so zum Ergebnis

$c={\frac {a\cdot \sin \gamma }{\sin \alpha }}\approx {\frac {5{,}4\,\mathrm {cm} \cdot \sin 65^{\circ }}{\sin 73^{\circ }}}\approx 5{,}1\,\mathrm {cm} .$

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de