Zeigermodell

Das Zeigermodell ist ein Konzept der Physik und insbesondere der Physikdidaktik. Es stellt periodische Vorgänge als Rotation eines Zeigers dar und findet vor allem in der Schwingungslehre, der Wechselstromlehre, der Wellenoptik und der Quantenmechanik Anwendung.

Der Zeiger dreht sich dabei meist zeitabhängig in der komplexen Ebene. Ein fester, zeitunabhängiger Zeiger wird in der komplexen Wechselstromrechnung verwendet, um den Phasenunterschied von Strom und Spannung in einem Stromkreis mit ohmschem Widerstand, Spule und Kondensator zu erklären. Manche Autoren bezeichnen die festen Zeiger als Phasor und verwenden dabei die in der Technik benutzte Versor-Schreibweise von komplexen Zahlen (Versor = „Dreher“).

Grundidee

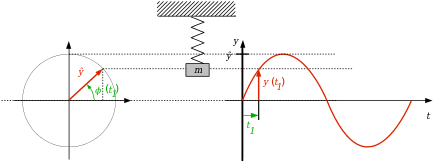
Das Zeigerdiagramm (links) am Beispiel eines Federpendels: Im Diagramm (rechts) wurde die Momentanauslenkung

des Pendels über der Zeit aufgetragen. Wie man sieht, entspricht sie der Projektion des Zeigers auf die y-Achse.

Ein Zeiger der Länge ${\hat {y}}$ dreht sich mit einer konstanten Winkelgeschwindigkeit $\omega$ um den Koordinatenursprung. Sein momentaner Winkel gegenüber der -Achse wird mit dem Formelzeichen $\varphi (t)$ bezeichnet.

Wenn man diesen Zeiger parallel zur -Achse mit einer Lampe anstrahlt, so wirft er einen Schatten der Länge y(t) auf eine senkrechte Wand. Es gilt dabei die einfache trigonometrische Beziehung

$y(t)={\hat {y}}\cdot \sin(\varphi (t))={\hat {y}}\cdot \sin(\omega t+\varphi _{0})$

wobei $\varphi _{0}$ der Startwinkel ist.^[1]

Die Veränderung des Schattens ist eine harmonische Schwingung. Dabei kommen den verwendeten Größen folgende Bedeutungen zu:

Formelzeichen	Einheit	Bedeutung im Zeigermodell	Bedeutung für die Schwingung
${\hat {y}}$	beliebig	Länge des Zeigers	Amplitude der Schwingung
	beliebig	„Schatten“ des Zeigers	Momentanauslenkung
$\varphi (t)$	$\mathrm {rad}$	Momentanwinkel	Phasenwinkel
$\varphi _{0}$	$\mathrm {rad}$	Startwinkel	Nullphasenwinkel
$\omega =2\pi f$	$\mathrm {\frac {rad}{s}}$	Winkelgeschwindigkeit	Kreisfrequenz
$f={\frac {1}{T}}$	$\mathrm {\frac {1}{s}}$	Drehzahl	Frequenz
	$\mathrm {s}$	Umlaufdauer	Periodendauer

Komplexe Zahlenebene

Veranschaulichung in der komplexen Zahlenebene

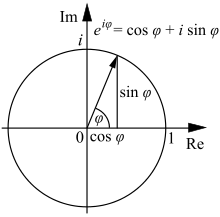
Häufig wird das Zeigermodell in der komplexen Zahlenebene dargestellt. Der Zeiger ${\underline {z}}$ ist dann eine komplexe Größe

${\underline {z}}=x+\mathrm {i} y$

mit dem Realteil $\mathrm {Re} \,{\underline {z}}=x$ und dem Imaginärteil $\mathrm {Im} \,{\underline {z}}=y$ . Mit der Eulerschen Formel lässt sich dann das Auslenkungs-Zeit-Gesetz der Schwingung wie folgt schreiben:

${\underline {z}}(t)={\hat {z}}\cdot \mathrm {e} ^{\mathrm {i} (\omega t+\varphi _{0})}={\hat {\underline {z}}}\cdot \mathrm {e} ^{\mathrm {i} \omega t}$

Die komplexe Größe ${\hat {\underline {z}}}={\hat {z}}\cdot \mathrm {e} ^{\mathrm {i} \varphi _{0}}$ wird manchmal auch als Phasor oder „komplexe Amplitude“ bezeichnet. Nimmt man von ${\underline {z}}(t)$ nur den Imaginärteil, so kommt man zu einer Gleichung wie aus dem vorangegangenen Abschnitt. Man kann aber ebenso gut mit dem Realteil arbeiten. An die Stelle der Sinusschwingung tritt dann die Kosinusschwingung. Da sich die Sinus- und Kosinusfunktionen nur durch den konstanten Phasenverschiebungswinkel von ${\tfrac {\pi }{2}}$ unterscheiden, sind beide mathematischen Formulierungen gleichwertig; innerhalb einer Problemstellung muss man sich jedoch entweder für die eine oder die andere Darstellung entscheiden.

Anwendungen

Elektrotechnik: Wechselstromlehre

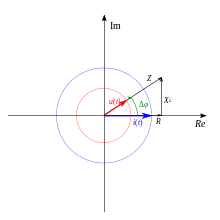
Wechselstrom und -spannung im Zeigermodell, hier am Beispiel einer Reihenschaltung des Widerstandes R und der Induktivität L. Die Zeiger von u und i rotieren um den Koordinatenursprung. Die Wirk-, Blind- und Scheinwiderstände (schwarze Pfeile, sie bilden das „Widerstandsdreieck“) ändern sich nicht.

→ Hauptartikel: Komplexe Wechselstromrechnung

In der Wechselstromlehre betrachtet man die sinusförmige Wechselspannung ${\underline {u}}(t)={\hat {u}}\cdot e^{\mathrm {j} (\omega t+\varphi _{u})}$ und die sinusförmige Wechselstromstärke ${\underline {i}}(t)={\hat {\imath }}\cdot e^{\mathrm {j} (\omega t+\varphi _{i})}$ .^[2] Beide können als Zeiger dargestellt werden, die gemeinsam mit der Winkelgeschwindigkeit $\omega$ um den Koordinatenursprung rotieren und dabei den konstanten Phasenverschiebungswinkel $\Delta \varphi =\varphi _{u}-\varphi _{i}$ aufweisen.

Wenn man analog zu der Beziehung $R={\frac {U}{I}}$ , die für Gleichströme gilt, die Gleichung

${\underline {Z}}={\frac {{\underline {u}}(t)}{{\underline {i}}(t)}}$

für Wechselströme und -spannungen aufstellt, erhält man die Impedanz, deren Betrag auch „Scheinwiderstand“ genannt wird. Man beachte, dass die Impedanz nicht zeitabhängig ist, denn der Faktor $e^{\mathrm {j} \omega t}$ kürzt sich heraus. Sie ist im allgemeinen Fall jedoch komplexwertig:

${\underline {Z}}=R+\mathrm {j} X$

Dabei ist der Realteil der ohmsche Widerstand oder Wirkwiderstand. Den Imaginärteil bezeichnet man als Blindwiderstand. Er setzt sich zusammen aus

dem induktiven Blindwiderstand $X_{L}=\omega L$ und
dem kapazitiven Blindwiderstand $X_{C}=-{\frac {1}{\omega C}}$

Der Vorteil der Darstellung sinusförmiger Wechselstromgrößen als komplexe Zeiger im Wechselstromdiagramm besteht darin, dass die wesentlichen Gesetze der Elektrizitätslehre (Verwendung der Impedanz wie ein Widerstand, Kirchhoffsche Regeln) auch in der Wechselstromlehre anwendbar bleiben, ohne dass komplizierte trigonometrische Berechnungen notwendig werden.

Hinweis: In der Praxis verwendet man in der Elektrotechnik für die Zeigerlänge (den Absolutbetrag) von Spannungen und Strömen statt der Amplitude ("Amplitudenzeiger") Û; Î oft den Effektivwert ("Effektivwertzeiger"): U; I.

Wellenoptik

Im eindimensionalen Fall wird eine Sinuswelle^[3] durch folgende Gleichung beschrieben:

$s(x,t)={\hat {s}}\cdot \sin(\omega t-kx)$

Dabei ist die Kreiswellenzahl $k={\frac {2\pi }{\lambda }}$ . Der Nullphasenwinkel soll der Einfachheit halber Null betragen.

Auch hier kann man sich die Momentanauslenkung durch einen rotierenden Zeiger vorstellen, wobei diesmal der Winkel nicht nur von der Zeit, sondern auch vom Ort abhängt. Betrachtet man die Welle an einem Ort, der sich eine Wellenlänge vom Ursprung entfernt befindet, so hat der Zeiger an diesem Ort eine Umdrehung weniger zurückgelegt als ein Zeiger im Koordinatenursprung. Man muss also von dem Winkel $\omega t$ jeweils das -fache der Entfernung abziehen.

Interferenz

→ Hauptartikel: Interferenz (Physik)

Interferenz im Zeigermodell: Dieses Schaubild zeigt eine Momentaufnahme zweier Sinuswellen (rot und blau) gleicher Amplitude und Frequenz, die interferieren. An einem bestimmten Punkt wurden die Zeiger beider Wellen exemplarisch gezeichnet.

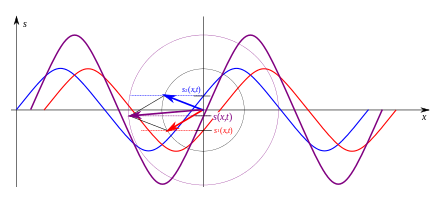
Überlagern sich an einem Punkt zwei Wellen, so müssen die Zeiger beider Wellen vektoriell addiert werden, wie dies in der nebenstehenden Abbildung exemplarisch für einen Punkt gezeichnet wurde. Die Momentanauslenkung der resultierenden Schwingung erhält man dann wieder durch Projektion des resultierenden (violetten) Zeigers auf die an dem gewünschten Punkt eingezeichnete senkrechte Achse. Die Länge dieses Zeigers gibt auch die Amplitude der resultierenden Welle an (violette Linie). Entscheidend für das Ergebnis der Interferenz ist also – neben den Amplituden der beteiligten Wellen – auch ihr Phasenunterschied $\Delta \varphi$ . Besonders einfach ist dies bei Wellen gleicher Frequenz, da hier der Phasenunterschied konstant ist.

Es gilt:

$\Delta \varphi =0,\,2\pi ,\,4\pi ,\,\dots$ : Konstruktive Interferenz. Die Amplituden der beiden Wellen addieren sich.
$\Delta \varphi =\pi ,\,3\pi ,\,5\pi ,\,\dots$ : Destruktive Interferenz. Die Amplituden der beiden Wellen müssen voneinander subtrahiert werden. Sind sie gleich, so löschen sie sich gegenseitig aus.

Überlagern sich in einem Punkt mehrere Wellen, so müssen die Zeiger aller Wellen vektoriell addiert werden.

Stehende Wellen

→ Hauptartikel: Stehende Welle

Stehende Wellen. Zwei gegenläufige Sinuswellen interferieren. Die rote Welle läuft nach rechts. Die blaue Welle läuft nach links. Die violetten Zeiger und Linien zeigen eine Momentaufnahme der resultierenden Welle. Die gestrichelten violetten Linien stehen für die Maximalausschläge. Erklärung s. Text.

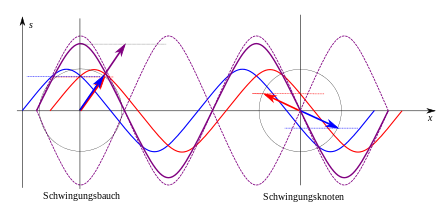
Überlagern sich zwei gegenläufige Wellen gleicher Frequenz, so entsteht eine stehende Welle. In der nebenstehenden Abbildung läuft die rote Welle nach rechts, die blaue Welle nach links. Greift man einen bestimmten Punkt heraus, so haben die Zeiger der beiden Wellen einen gewissen Phasenunterschied. Dieser Unterschied hängt nicht von der Zeit ab, da sich beide Zeiger gleich schnell in dieselbe Richtung drehen. Trotzdem hängt er vom Ort ab. An Orten, wo der Phasenunterschied $0$ oder $2\pi$ beträgt – wo also die beiden Welle in Phase sind – ist die Momentanauslenkung verglichen mit anderen Orten stets maximal. Man nennt dies einen „Schwingungsbauch“. An den Stellen, wo der Phasenunterschied $\pm \pi$ ist, gibt es überhaupt keine Auslenkung. Dies nennt man „Schwingungsknoten“. Da sich weder die Schwingungsbäuche noch die Schwingungsknoten bewegen, hat es den Anschein, als breite sich die Welle überhaupt nicht aus, daher der Name „stehende Welle“. Der Maximalausschlag der stehenden Welle an einem Schwingungsbauch ist durch die Summe der Zeigerlängen, sprich: die Summe der Amplituden gegeben.

Beugung

→ Hauptartikel: Beugung (Physik)

Bei mehrdimensionalen Problemen (z.B. Einfachspalt, Doppelspalt, optisches Gitter, …) muss berücksichtigt werden, dass Wellen, die an einem Punkt zusammentreffen, unterschiedliche Wege zurückgelegt haben können. Man berechnet dann die Gangunterschiede. Ein Gangunterschied $\delta$ ist gleichbedeutend mit einem Phasenunterschied von $\Delta \varphi =k\delta$ . Man erhält das Beugungsmuster also durch Vektoraddition der Zeiger der interferierenden Wellen unter Berücksichtigung des durch den Gangunterschied entstehenden Phasenunterschieds.

Grenzen

Während sich Phasenunterschiede und ihre Auswirkungen auf die Interferenz mit dem Zeigermodell sehr gut erklären lassen, versagt es bei der Berechnung der Amplituden, da weder die Dämpfung noch die Verteilung einer Welle im Raum durch das Zeigermodell berücksichtigt werden können. Diese Schwäche haben aber auch alternative Konzepte, z.B. die Elementarwellen nach Huygens und Fresnel.

Quantenmechanik

Auch die Wellenfunktion der Quantenmechanik lässt sich im Zeigermodell darstellen. Feynman nennt die (komplexe) Länge des Zeigers „Wahrscheinlichkeitsamplitude“, da ihr Betragsquadrat nach den Regeln der Quantenmechanik ein Maß für die Wahrscheinlichkeitsdichte (z.B. für das Auffinden eines Teilchens) ist. Dabei kommt es ebenso zum Effekt der Interferenz, wie dies im Abschnitt Wellenoptik weiter oben beschrieben wurde. Wenn ein Quantenobjekt eine Versuchsanordnung durchläuft, müssen die Wahrscheinlichkeitsamplituden für alle möglichen Wege vektoriell addiert werden. Damit findet Feynman eine anschauliche Interpretation für die Methode der Pfadintegrale.

Anmerkungen

↑ Auf diese Weise werden die Schwingungen in vielen Schulbüchern der gymnasialen Oberstufe eingeführt, z. B. in Dorn, Bader: Physik Gymnasium(G8) 11/12. Schroedel, 2010, ISBN 978-3-507-10748-9; Meyer, Schmitt: Lehrbuch Physik, Gymnasiale Oberstufe. Duden, 2011, ISBN 978-3-8355-3311-0; Boysen u. a.: Oberstufe Physik Gesamtband. Cornelsen, 1999, ISBN 3-464-03440-2.
↑ In der Wechselstromlehre wird die imaginäre Einheit als $\mathrm {j}$ geschrieben, um Verwechslungen mit der Stromstärke zu vermeiden.
↑ Im Abschnitt „Wellenoptik“ wird hier – wie in der Schulphysik üblich – eine Darstellung mit reellen Zeigern verwendet. Wenn mit komplexen Zahlen gearbeitet wird, tritt an die Stelle der Sinusfunktion die komplexe e-Funktion, wie dies im Abschnitt „Komplexe Zahlenebene“ beschrieben wurde. Die hier verwendete Vektoraddition entspricht der Addition komplexer Zahlen.

Basierend auf einem Artikel in:

Wikipedia.de