Studentsche t-Verteilung
Die studentsche t-Verteilung (auch Student-t-Verteilung oder kurz t-Verteilung) ist eine Wahrscheinlichkeitsverteilung, die 1908 von William Sealy Gosset entwickelt und nach seinem Pseudonym Student benannt wurde.
Er hatte festgestellt, dass die standardisierte
Schätzfunktion
des Stichproben-Mittelwerts normalverteilter
Daten nicht mehr normalverteilt, sondern t-verteilt ist, wenn die zur Standardisierung
des Mittelwerts benötigte Varianz
des Merkmals unbekannt ist und mit der Stichprobenvarianz
geschätzt werden muss. Die t-Verteilung erlaubt die Berechnung der Verteilung
der Differenz vom Mittelwert der Stichprobe zum wahren Mittelwert der Grundgesamtheit.
Die t-Werte
hängen ab vom Signifikanzniveau
und vom Stichprobenumfang
und bestimmen das Vertrauensintervall
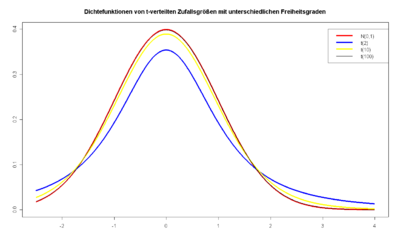
und damit die Aussagekraft der Schätzung des Mittelwertes. Die t-Verteilung wird
mit wachsendem
schmaler und geht für
in die Normalverteilung über (siehe Grafik rechts). Hypothesentests, bei
denen die t-Verteilung Verwendung findet, bezeichnet man als t-Tests.
Die Herleitung wurde erstmals 1908 veröffentlicht, während Gosset in einer Guinness-Brauerei arbeitete. Da sein Arbeitgeber die Veröffentlichung nicht gestattete, veröffentlichte Gosset sie unter dem Pseudonym Student. Der t-Faktor und die zugehörige Theorie wurden erst durch die Arbeiten von R. A. Fisher belegt, der die Verteilung Student’s distribution (Students Verteilung) nannte.
Definition
Eine stetige Zufallsvariable
genügt der studentschen t-Verteilung mit
Freiheitsgraden,
wenn sie die Wahrscheinlichkeitsdichte
für
besitzt. Dabei ist
die Gamma-Funktion.
Alternativ lässt sich die t-Verteilung mit
Freiheitsgraden auch definieren als die Verteilung der Größe
wobei
eine standardnormalverteilte
Zufallsvariable ist, und
eine, von
unabhängige,
-verteilte
Zufallsvariable mit
Freiheitsgraden bedeutet.
Verteilung
Die Verteilungsfunktion lässt sich geschlossen ausdrücken als
oder als
mit
wobei
die Betafunktion
darstellt.
berechnet die Wahrscheinlichkeit dafür, dass eine gemäß
verteilte Zufallsvariable
einen Wert kleiner oder gleich
erhält.
Eigenschaften
Es sei
eine t-verteilte Zufallsvariable mit
Freiheitsgraden und Dichte
.
Wendepunkte
Die Dichte besitzt Wendepunkte bei
Median
Der Median ist
Modus
Der Modus ergibt sich zu
Symmetrie
Die Studentsche t-Verteilung ist symmetrisch um die 0.
Erwartungswert
Für den Erwartungswert
erhält man für
Der Erwartungswert für
existiert nicht.
Varianz
Die Varianz
ergibt sich für
zu
Schiefe
Die Schiefe
ist für
Wölbungen
Für die Kurtosis-Wölbung
und die Exzess-Wölbung
erhält man für
Momente
Für die -ten
Momente
und die
-ten
zentralen Momente
gilt:
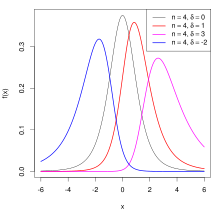
Nichtzentrale t-Verteilung
Die Größe
mit
und
als Nichtzentralitätsparameter
folgt der sogenannten nichtzentralen t-Verteilung.
Diese Verteilung wird vor allem zur Bestimmung des β-Fehlers bei
Hypothesentests mit
t-verteilter Prüfgröße
verwendet. Ihre Wahrscheinlichkeitsdichte lautet:
Die Klammer mit der Summe hypergeometrischer Funktionen lässt sich noch etwas einfacher schreiben, sodass ein kürzerer alternativer Ausdruck für die Dichte entsteht:
wobei
ein Hermitesches
Polynom mit negativem Index darstellt mit
.
Der Erwartungswert liegt für
bei
und die Varianz (für )
bei
Mit
erhält man die Kennwerte der zentralen t-Verteilung.
Beziehung zu anderen Verteilungen
Beziehung zur Cauchy-Verteilung
Für
und mit
ergibt sich die Cauchy-Verteilung
als Spezialfall aus der Studentschen t-Verteilung.
Beziehung zur χ²-Verteilung und Standardnormalverteilung
Die t-Verteilung beschreibt die Verteilung eines Ausdruckes
wobei
eine standardnormalverteilte
und
eine χ²-verteilte
Zufallsvariable mit
Freiheitsgraden bedeutet. Die Zählervariable muss unabhängig von der
Nennervariable sein. Die Dichtefunktion der t-Verteilung ist dann symmetrisch
bezüglich ihres Erwartungswertes 0. Die Werte der Verteilungsfunktion liegen in
der Regel tabelliert vor.
Näherung durch die Normalverteilung
Mit steigender Zahl von Freiheitsgraden kann man die Verteilungswerte der t-Verteilung mit Hilfe der Normalverteilung annähern. Als Faustregel gilt, dass ab 30 Freiheitsgraden die t-Verteilungsfunktion durch die Normalverteilung approximiert werden kann.
Verwendung in der mathematischen Statistik
Verschiedene Schätzfunktionen sind t-verteilt.
Wenn die unabhängigen Zufallsvariablen
identisch normalverteilt sind mit Erwartungswert
und Standardabweichung
,
kann bewiesen werden, dass der Stichprobenmittelwert
und die Stichprobenvarianz
stochastisch unabhängig sind.
Weil die Zufallsgröße
eine Standardnormalverteilung hat und
einer Chi-Quadrat-Verteilung
mit
Freiheitsgraden folgt, ergibt sich, dass die Größe
nach Definition
t-verteilt ist mit
Freiheitsgraden.
Also ist der Abstand des gemessenen Mittelwertes vom Mittelwert der
Grundgesamtheit verteilt wie .
Damit berechnet man dann das 95-%-Konfidenzintervall
für den Mittelwert
zu
wobei
durch
bestimmt ist. Dieses Intervall ist für
etwas größer als dasjenige, welches sich mit bekanntem
aus der Verteilungsfunktion der Normalverteilung bei gleichem Konfidenzniveau
ergeben hätte
.
Herleitung der Dichte
Die Wahrscheinlichkeitsdichte der t-Verteilung lässt sich herleiten aus der
gemeinsamen Dichte der beiden unabhängigen Zufallsvariablen Z und ,
die standardnormal, beziehungsweise Chi-Quadrat-verteilt sind:
Mit der Transformation
bekommt man die gemeinsame Dichte von
und
,
wobei
und
.
Die Jacobideterminante dieser Transformation ist:
Der Wert
ist unwichtig, weil er bei der Berechnung der Determinante mit 0 multipliziert
wird. Die neue Dichtefunktion schreibt sich also
Gesucht ist nun die Randverteilung
als Integral über die nicht
interessierende Variable v:
Ausgewählte Quantile der t-Verteilung
Tabelliert sind t-Werte für verschiedene Freiheitsgrade
und gebräuchliche Wahrscheinlichkeiten
(0,75 bis 0,999), wofür gilt:
Aufgrund der Spiegelsymmetrie der Dichte braucht man für den Fall des
beidseitig symmetrisch begrenzten Intervalls nur die Wahrscheinlichkeitsskala
anzupassen. Dabei verringern sich die Wahrscheinlichkeiten bei gleichem ,
denn das Integrationsintervall wird durch Wegschneiden des Bereichs von
bis
reduziert:
Werden bei einer Stichprobe
Beobachtungen durchgeführt und aus der Stichprobe
Parameter geschätzt, so ist
die Anzahl der Freiheitsgrade.
Zu der Anzahl von Freiheitsgraden
in der ersten Spalte und dem Signifikanzniveau
(dargestellt als
in der zweiten Zeile) wird in jeder Zelle der folgenden Tabelle der Wert des
(einseitigen) Quantils
,
entsprechend DIN 1319-3, angegeben. Dies erfüllt für die Dichte
der
-Verteilung
die folgenden Gleichungen:
- Einseitig:
- Zweiseitig:
Also findet man beispielsweise mit
und
die t-Werte von 2,776 (zweiseitig) oder 2,132 (einseitig).
Die Quantilfunktion der t-Verteilung
ist die Lösung der Gleichung
und damit prinzipiell über die Umkehrfunktion zu berechnen. Konkret gilt
hier
mit
als Inverse der regularisierten unvollständigen Betafunktion. Dieser Wert
ist in der Quantiltabelle
unter den Koordinaten p und n eingetragen.
Für wenige Werte
(1,2,4) vereinfacht sich die Quantilfunktion:
Tabelle einiger t-Quantile
| Anzahl Freiheitsgrade n |
P für zweiseitigen Vertrauensbereich | |||||||
|---|---|---|---|---|---|---|---|---|
| 0,5 | 0,75 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | 0,998 | |
| P für einseitigen Vertrauensbereich | ||||||||
| 0,75 | 0,875 | 0,90 | 0,95 | 0,975 | 0,99 | 0,995 | 0,999 | |
| 1 | 1,000 | 2,414 | 3,078 | 6,314 | 12,706 | 31,821 | 63,657 | 318,309 |
| 2 | 0,816 | 1,604 | 1,886 | 2,920 | 4,303 | 6,965 | 9,925 | 22,327 |
| 3 | 0,765 | 1,423 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 | 10,215 |
| 4 | 0,741 | 1,344 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 | 7,173 |
| 5 | 0,727 | 1,301 | 1,476 | 2,015 | 2,571 | 3,365 | 4,032 | 5,893 |
| 6 | 0,718 | 1,273 | 1,440 | 1,943 | 2,447 | 3,143 | 3,707 | 5,208 |
| 7 | 0,711 | 1,254 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 | 4,785 |
| 8 | 0,706 | 1,240 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 | 4,501 |
| 9 | 0,703 | 1,230 | 1,383 | 1,833 | 2,262 | 2,821 | 3,250 | 4,297 |
| 10 | 0,700 | 1,221 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 | 4,144 |
| 11 | 0,697 | 1,214 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 | 4,025 |
| 12 | 0,695 | 1,209 | 1,356 | 1,782 | 2,179 | 2,681 | 3,055 | 3,930 |
| 13 | 0,694 | 1,204 | 1,350 | 1,771 | 2,160 | 2,650 | 3,012 | 3,852 |
| 14 | 0,692 | 1,200 | 1,345 | 1,761 | 2,145 | 2,624 | 2,977 | 3,787 |
| 15 | 0,691 | 1,197 | 1,341 | 1,753 | 2,131 | 2,602 | 2,947 | 3,733 |
| 16 | 0,690 | 1,194 | 1,337 | 1,746 | 2,120 | 2,583 | 2,921 | 3,686 |
| 17 | 0,689 | 1,191 | 1,333 | 1,740 | 2,110 | 2,567 | 2,898 | 3,646 |
| 18 | 0,688 | 1,189 | 1,330 | 1,734 | 2,101 | 2,552 | 2,878 | 3,610 |
| 19 | 0,688 | 1,187 | 1,328 | 1,729 | 2,093 | 2,539 | 2,861 | 3,579 |
| 20 | 0,687 | 1,185 | 1,325 | 1,725 | 2,086 | 2,528 | 2,845 | 3,552 |
| 21 | 0,686 | 1,183 | 1,323 | 1,721 | 2,080 | 2,518 | 2,831 | 3,527 |
| 22 | 0,686 | 1,182 | 1,321 | 1,717 | 2,074 | 2,508 | 2,819 | 3,505 |
| 23 | 0,685 | 1,180 | 1,319 | 1,714 | 2,069 | 2,500 | 2,807 | 3,485 |
| 24 | 0,685 | 1,179 | 1,318 | 1,711 | 2,064 | 2,492 | 2,797 | 3,467 |
| 25 | 0,684 | 1,178 | 1,316 | 1,708 | 2,060 | 2,485 | 2,787 | 3,450 |
| 26 | 0,684 | 1,177 | 1,315 | 1,706 | 2,056 | 2,479 | 2,779 | 3,435 |
| 27 | 0,684 | 1,176 | 1,314 | 1,703 | 2,052 | 2,473 | 2,771 | 3,421 |
| 28 | 0,683 | 1,175 | 1,313 | 1,701 | 2,048 | 2,467 | 2,763 | 3,408 |
| 29 | 0,683 | 1,174 | 1,311 | 1,699 | 2,045 | 2,462 | 2,756 | 3,396 |
| 30 | 0,683 | 1,173 | 1,310 | 1,697 | 2,042 | 2,457 | 2,750 | 3,385 |
| 40 | 0,681 | 1,167 | 1,303 | 1,684 | 2,021 | 2,423 | 2,704 | 3,307 |
| 50 | 0,679 | 1,164 | 1,299 | 1,676 | 2,009 | 2,403 | 2,678 | 3,261 |
| 60 | 0,679 | 1,162 | 1,296 | 1,671 | 2,000 | 2,390 | 2,660 | 3,232 |
| 70 | 0,678 | 1,160 | 1,294 | 1,667 | 1,994 | 2,381 | 2,648 | 3,211 |
| 80 | 0,678 | 1,159 | 1,292 | 1,664 | 1,990 | 2,374 | 2,639 | 3,195 |
| 90 | 0,677 | 1,158 | 1,291 | 1,662 | 1,987 | 2,368 | 2,632 | 3,183 |
| 100 | 0,677 | 1,157 | 1,290 | 1,660 | 1,984 | 2,364 | 2,626 | 3,174 |
| 200 | 0,676 | 1,154 | 1,286 | 1,653 | 1,972 | 2,345 | 2,601 | 3,131 |
| 300 | 0,675 | 1,153 | 1,284 | 1,650 | 1,968 | 2,339 | 2,592 | 3,118 |
| 400 | 0,675 | 1,152 | 1,284 | 1,649 | 1,966 | 2,336 | 2,588 | 3,111 |
| 500 | 0,675 | 1,152 | 1,283 | 1,648 | 1,965 | 2,334 | 2,586 | 3,107 |
| 0,674 | 1,150 | 1,282 | 1,645 | 1,960 | 2,326 | 2,576 | 3,090 | |


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.03. 2020